【模板题】【并查集】 3道经典例题+一道练习——注意维系多个集合的技巧

并查集入门：PID331 / 家族——并查集

题目大意：n个人中有m对亲戚关系，之后询问p对是否有亲戚关系
注意：
1、初始化Tree[i]=-1
2、在合并两个集合时要先判断是否在一个集合(x1!=x2)

#include
#include
#include
using namespace std;
int n,m,p;
int Tree[5001];
int findfa(int x)
{
	if (Tree[x]==-1)
		return x;
	int temp=findfa(Tree[x]);
	Tree[x]=temp;
	return temp;
}

int main()
{
	int i,a,b,x1,x2;
	cin>>n>>m>>p;
	for (i=1;i<=n;i++)//初始化
		Tree[i]=-1;
	for (i=0;i>a>>b;
		x1=findfa(a);
		x2=findfa(b);
		if (x1!=x2)//别忘了判断！
			Tree[x1]=x2;
	}
	for (i=1;i<=p;i++)
	{
		cin>>a>>b;
		if (findfa(a)!=findfa(b))
			cout<<"No"<

并查集提高1：[NOIP2010]关押罪犯——并查集，最小生成树变形

题目大意：N个人有M对关系值，值越大越不能分到一起，只能分成两堆，求按要求分堆后堆中的最大关系值

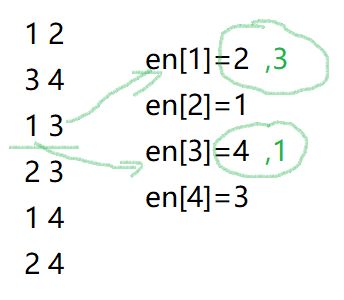
思路：按关系值从大到小排序，假设1有x个关系对象，则按序把x（即敌人）合并到一个堆中。en数组表示每一个人的敌人代表，相当于一个子树的树根，一开始需要定义一个敌人代表，之后把其他敌人与其合并。若发现两者已经在一个集合中则输出答案。——这个思路易理解，但是操作繁琐。推荐下面那道题使用的维系多个集合的方法。

#include
#include

【模板题】并查集提高2：[NOI2001]食物链——并查集+维系多个集合

题目大意：N个动物分为三类：A吃B，B吃C，C吃A，按顺序输入K条语句判断对错。“1 x y”表示x、y同类；“2 x y”表示x吃y。
对于假话的定义：
1.当前的话与前面的某些真的话冲突，就是假话；
2.当前的话中X或Y比N大，就是假话；
3.当前的话表示X吃X，就是假话。

求假话个数。

思路：维持一个3*N大小的数组，每种动物都有与自己有关系的ABC集合，x表示他是A，x+n表示他是B，x+2*n表示他是C。
1）为同一物种时，即与之有关系的三类一一对应，就把他们的当A、B、C都并到一个集合。在判断错误时，仅需错一位、错两位判断即可。
A1 B1 C1
A2 B2 C2
2）当两个生物为捕食关系时，即发生错位，合并如下关系即可。同样判断错误错一位、错两位判断。
A1 B1 C1

B2 C2 A2

注意：
1、针对此题初始化Tree[i]=i省麻烦

2、合并一定记得x!=y!!!!

#include
using namespace std;
int Tree[150010];
int findfa(int x)
{
	if (Tree[x]==x)
		return x;
	int temp=findfa(Tree[x]);
	Tree[x]=temp;
	return temp;
}
void getTogether(int a,int b)
{
	int x=findfa(a);
	int y=findfa(b);
	if (x!=y)//!!!!!!!!!!!!!!!!!!!!!!!1
		Tree[x]=y;
}
int main()
{
	int N,K,i,opt,x,y;
	cin>>N>>K;
	for (i=0;i<=N*3;i++)
		Tree[i]=i;
	int ans=0;
	for (i=1;i<=K;i++)
	{
		cin>>opt>>x>>y;
		if (x>N || y>N || (opt==2 && x==y))
		{
			ans++;continue;
		}
		if (opt==1)
		{    
			if (x==y)	continue;//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
			if ( (findfa(x)==findfa(y+N)) ||(findfa(x)==findfa(y+2*N)))
				ans++;
			else
			{
				getTogether(x,y);
				getTogether(x+N,y+N);
				getTogether(x+2*N,y+2*N);
			}
		}
		else //opt==2
		{  
			if ( (findfa(x)==findfa(y)) || (findfa(x)==findfa(y+2*N)) )
				ans++;
			else
			{
				getTogether(x,y+N);
				getTogether(x+N,y+2*N);
				getTogether(x+2*N,y);
			}
		}
	}
	cout<

练习：PID577 / 团伙

题目大意：我朋友的朋友是我的朋友。我敌人的敌人也是我的朋友。

两个强盗是同一团伙的条件是当且仅当他们是朋友。共N个强盗，M个关系，F表示p和q是朋友，E表示敌人，问你最多有多少个强盗团伙。

思路：参照上一题维系两个集合的思路（也可以采用en数组）

注意：为敌人时Together(p+N,q)一定是“+N”的在前面，因为由p+N指向q，第一轮（仅出现敌人）1~N关系不变，之后再出现敌人的敌人才会改变1~N的合并关系。这样才能提供最大团伙数。和采用en数组道理一样，第一次出现是初始化，后面才合并。

#include
using namespace std;
int Tree[2010];
int N,M;
int findfa(int x)
{
	if (Tree[x]==x)
		return x;
	int temp=findfa(Tree[x]);
	Tree[x]=temp;
	return temp;
}
void Together(int a,int b)
{
	int x=findfa(a);
	int y=findfa(b);
	if (x!=y)
		Tree[x]=y;
}
int main()
{
	cin>>N>>M;
	char opt;
	int i,p,q;
	for (i=1;i<=2*N;i++)
		Tree[i]=i;
	for (i=0;i>opt>>p>>q;
		if (opt=='F')
			Together(p,q);
		else
		{
			Together(p+N,q);//这边的顺序不能换！将p+N指向q
			Together(q+N,p);//将q+N指向p
		}
	}
	int ans=0;
	for (i=1;i<=N;i++)
		if (Tree[i]==i)
			ans++;
	cout<