【贪心算法（一）】贪心算法基础

1介绍

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。与动态规划不同的是，贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

2部分背包问题

2.1解析

问题：我们有四种物品，他们的重量和价格分别是10, 5, 30,20 kg和60, 100, 120,40。
可以选择一些物体的一部分（比如盐，米）使在总重量不超过背包总重量V的条件下总价值最大。
（1） 既然可以只选取一部分，也就是一个单位一个单位的选取，比如，10kg米，我只选1kg米放进我的背包。这意味着，只要选取单位价格最高的，对应价值也就越高。
（2） 先计算出对应物品的单位价格，然后排序，记住要把其它数组也对应上，比如题目中第二种物品单位价格最高，会被排到第一位，那么的重量数组和价格数组也要排到第一位。这样可以方便计算价格。

2.2源码

#include
using namespace std;
#define N 4
#define W 44 //背包总重量
int main(){
	int V[N]={10,5,30,20};//重量
	int P[N]={60,100,120,40};//价格
	double Vp[N];//每种物品单位重量的价格
	int i,j,temp;//循环用
    int SumW=0;//记录重量
	int Vlaue=0;//记录价格
	int SumTemp=0;//临时记录总和，用于切换Vp数组
	//求单位重量价格
	for(i=0;i=W)
				break;
		}
		SumW+=SumTemp;
		Vlaue+=SumTemp*Vp[i];
		SumTemp=0;
		i++;
	}
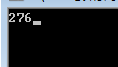
	cout <

2.3结果

输出:276=20*5+6*10+4*29;

5+10+29=44

3乘船问题_重量

3.1解析

问题：有n个人，第i个人重量为wi。每艘船的最大载重量均为C，且最多只能乘两个人。用最少的船装载所有人。

（1）      船最少为n/2艘，所以尽量让每艘船载两个人。

（2）      设某人有最轻重量W0，那么将最重重量为W1的人放上去，如果W1+W0>C,那么W1只能独自坐一艘，并且从剩下的人中找最重的。如果W1+W0<=C,那么让他俩乘一艘，并且从剩下的人中再找最轻和最重的

（3）      重复步骤（2），直到所有人都走完，比较重要的一点是下面这段代码

while(i<=j){
		if(W[i]+W[j]<=C && i

（4）      i++表示剩下的人中最轻的上船，j--表示剩下的人中最重的上船，不管怎么样每次循环最重的都会上船，所以每次TotalCount++;

3.2源码

测试三组数据：

No1：C=100，N=8，W={1,2,3,4,5,6,7,8};//任意数字

No2：C=100，N=5，W={10,50,60,70,75};//奇数个

No3：C=100，N=8，W={10,25,60,70,75,80,100,110};//偶数个

#include
using namespace std;
#define Max 20
//冒泡排序
void Sort(int *p,int n){
	int i,j,temp;
	for (i = 0; i < n; i++)  
    {  
        for (j = i + 1; j < n; j++)  
        {  
            if (*(p+i)> *(p+j))  
            {  
                temp=*(p+i);
				*(p+i)=*(p+j);
				*(p+j)=temp;
            }  
        }  
    }  
}
int main(){
	int C,N;//C为每艘船最大载重量，N为总人数
	int W[Max];//每个人重量
	int TotalCount=0;//船的总条数
	int i ,j;
	cin>>C>>N;
	for(i=0;i>W[i];
	}
	//从小到大排序
	Sort(W,N);
	//选择
	j=N-1;
	i=0;
	while(i<=j){
		if(W[i]+W[j]<=C && i

3.3结果

测试的三组组数据：

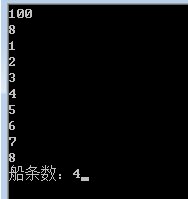
No1：C=100，N=8，W={1,2,3,4,5,6,7,8};TotalCount=4；

组合：(1,8),(2,7),(3,6),(4,5)

No2：C=100，N=5，W={10,50,60,70,75};TotalCount=4；

组合：(10,75),(70),(60),(50)

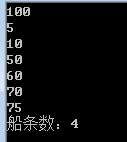
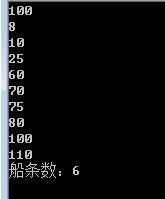
No3：C=100，N=8，W={10,25,60,70,75,80,100,110};TotalCount=6；

组合：(110),(100),(10,80),(25,75),(70),(60)

4乘船问题_速度

4.1解析

问题：只有一艘船，能乘2人，船的运行速度为2人中较慢一人的速度，过去后还需一个人把船划回来，问把n个人运到对岸，速度为Vi，最少需要多久。
（1） 把存储个人时间的数组升序排序，假设n-1和n-2两人过河，速度一定是最慢的。如何让最慢的这两个人（每次取数组最后的两个老兄）过河的时间最少？也就能得到最少时间。
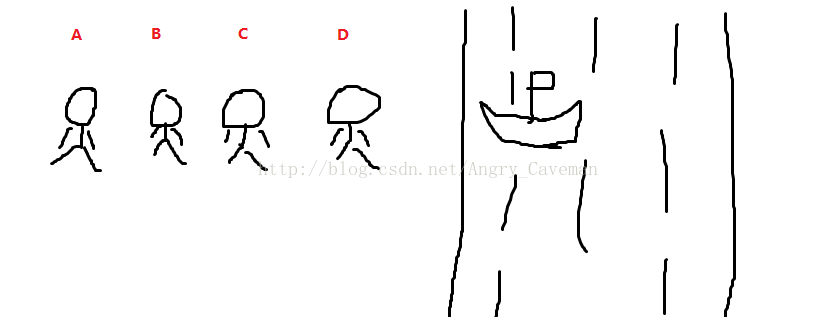
（2） 有两种情况：设A，B，C，D四人，A,B为速度最快和次快的，C,D为速度次慢和最慢的。

（1）      第一种情况：A送D过河，A回来，A送C过河，A回来；

得到方程：2*Arry[0]+Arry[n-2]+Arry[n-1]

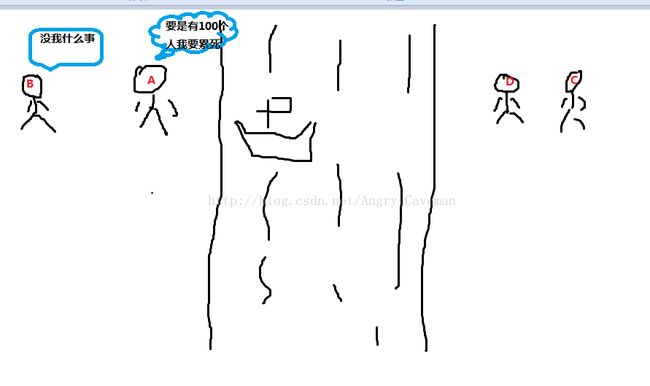
（4） 第二种情况：A送B过去，A回来，C，D一起过去，B回来
得到方程：Arry[0]+2*Arry[1]+Arry[n-1]

4.2源码

#include 
using namespace std;
#define Max 20
//冒泡排序
void Sort(int *p,int n){
	int i,j,temp;
	for (i = 0; i < n; i++){  
        for (j = i + 1; j < n; j++){  
            if (*(p+i)> *(p+j)){  
                temp=*(p+i);
				*(p+i)=*(p+j);
				*(p+j)=temp;
            }  
        }  
    }  
}
int min(int a ,int b){
	if(a>b)
		return b;
	else
		return a;
}
int main(){
	int n;//n个人
	int i,j;//循环用
	int Arry[Max];//存储每个人速度
	int sum=0;
	cin>>n;
	for(i=0;i>Arry[i];
	}
	//排序
	Sort(Arry,n);
	//选择，每次运送耗时最长的一组乘客,也就是最后两位
	//有两种情况既能把耗时最长的送走，同时确保此次运送整体时间最短。
	//1,Arry[0]+2*Arry[1]+Arry[n-1];2,2*Arry[0]+Arry[n-2]+Arry[n-1]
	  while(n>3){  
            sum+=min(Arry[0]+2*Arry[1]+Arry[n-1],2*Arry[0]+Arry[n-2]+Arry[n-1]);  
            n-=2;  
      }  
      if(n==3) sum+=Arry[0]+Arry[1]+Arry[2];  
      else if(n==2) sum+=Arry[1];  
      else sum+=Arry[0];  
	  cout<

4.3结果

（1）      min（1*2+6+7=16，1+2*2+7=12）=12；

（2）      min（1*2+4+5=11，1+2*2+5=10）=10；

（3）      min（1+2+3=6）=6；

（4）      sum=12+10+6=28

5总结

这是贪心算法的基础问题，通过以上直击心灵深处的灵魂式绘图，应该很容易理解，应该能有一个大体的意识了，贪心算法会记上三节，最后一节挂上全部项目的Github源码链接。