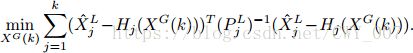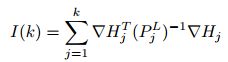OpenSLAM之2D I-SLSJF阅读、翻译、分析（一）

最近看OpenSLAM的一些slam算法，学习一下，顺便做一下翻译，网址：https://openslam-org.github.io/

本篇介绍2D I-SLASJF：

定义：I-SLSJF:Iterated-a sequence local submap joining filter 局部子图迭代插入算法

I-SLSJF 是一个使用稀疏信息滤波与最小二乘法优化方法的局部子图插入算法 ，该算法的输入是一系列局部子图，输出是全局地图；Victoria Park 数据和DLR-Spatial-Cognition 数据很好的使算法起作用。

作者：悉尼科技大学（世界排名250左右） 自治系统中心 工程与信息技术学院 副教授 （shoudong huang 黄守东？） ，其研究方向：非线性控制系统、移动机器人实时构图、导航等技术。

算法详细描述：本算法是一种新的用来建立大范围特征地图的 局部子图插入算法，这是基于近年来先进的稀疏局部子图滤波器和多种迭代法进行估计改善因此这种方法称作Iterated SLSJF(I-SLSJF). 算法输入的是一系列子图，输出的是全局地图（包含有所有特征的全局位置，包含各个局部子图中机器人开始和结束的位置），这里也提供了一些实时、实验数据和matlab 源码，各位使用者可以下载下来进行测试（源码地址：https://github.com/OpenSLAM-org/openslam_2d-i-slsjf）。

输入数据：系列局部子图，每一个子图含有状态向量估计和协方差矩阵

地图类型：点特征图

算法测试需求：matlab

论文来源：Iterated SLSJF: A sparse local submap joining algorithm with improved consistency 链接

                  Sparse local submap joining filter for building large-scale maps 链接

两篇都是2008年，比较早。

论文分析：...等我再写，稍等

matlab源码分析：...稍等

论文详译：Iterated SLSJF: A sparse local submap joining algorithm with improved consistency

作者：澳大利亚悉尼-黄守东

摘要：

        本文用来展示一种新的基于构建大尺度特征地图的局部子图插入算法。该算法是基于之前的SLSJF(Sparse Local Submap Joining Filter稀疏子图插入法)算法前提下，然后进一步采用迭代法改善估计效果，现在称作Iterated-SLSJF。本算法输入一系列局部子图，输出全局地图，其中全局地图中包含有所有特征的位置和子图中机器人的起始终止坐标。

          在I-SLSJF算法的局部子图插入中，无论何时通过扩展信息滤波法计算的位姿变化量超过预设值时，所有子图的信息矢量、信息矩阵都会重新计算，这改善了估计的精确度以及减少了雅克比矩阵在相同特征上产生不同值的可能性（这也是EIF和EKF算法不一致性的主要原因）。此外，尽管I-SLSJF比SLSJF的计算花销大，也不失为一种提高稀疏矩阵效率的补充手段。本算法通过放在及实验的方法与EKF SLAM、SJSJF进行了比较。

1简介：

        SLAM特色是在建立环境的特征地图的同时对机器人的位置姿态进行估计的过程。局部子图插入算法提供了一个建立大尺度地图的有效方法，在该方法中，系列小尺寸的局部图建立，然后结合成全局图。

        在EKF时序图插入过程中，地图结果的协方差矩阵有比较多的相互关系。因此EKF地图融合过程有较高的计算需求，由于全局地图更新频率的下降，计算结果全部得以获得。

        在我们之前的研究工作中，事实证明局部子图插入算法可以使用稀疏信息滤波器完成。SLSJF结合了局部子图插入算法和SLAM的稀疏性然后大大减少了构建全局地图的计算花销。

         基于策略的局部子图能够改善SLAM的一致性，仿真结果表明在许多情况下SLSJF算法相比于单EKF SLAM而言，一致性更好，然而，当状态估计误差较大的时候，线性假设情况下的EIF公式可能会出错，今儿导致SLSJF出现非一致性。

        在SLSJF中，所有机器人的起始终止位姿都在全局状态向量中，在EIF中没有预测的步骤，因此，可以采用最小均方差对估计问题进行优化，然后在每一个融合步骤上进行迭代处理。

       在本文中，我们提出了I-SLSJF算法，该算法必要时在每个地图融合时通过EIF开始多重线性最小均方差迭代，尤其是在每一个步地图融合中，如果状态改变量超过阈值，然后信息矩阵和信息向量都会在所有子图数据支持下重新计算，这样可以改善一致性，尽管I-SLSJF与SLSJF相比需要更多的计算资源，但是依然是一种有效的方法。

        本文按照以下方式组织：第二部分简介SLSJF算法的关键点，第三部分详细描述了I-SLSJF算法，第四部分展示仿真与实验结果，第五部分讨论一些相关工作，第六部分结论。

2SLSJF介绍

        这部分回顾了SLSJF算法。SLSJF结合一个局部区域的一系列地图，地图是由传统SLAM算法建立的。

2.1 使用局部子图作为激光数据

       当把子图融合进全局地图中时，SLSJF把每一个局部子图看成一个激光数据，因此，从机器人起始位姿到局部特征和终点位姿，局部子图相当提供了一个连续的相对位置变化，这个子图可以定义为：一个激光数据，包含有起点位置及所有局部特征以及一个虚拟的终点机器人位置。观测值是局部子图估计。观测噪声与局部子图相同的协方差矩阵的0期望高斯噪声。

2.2稀疏信息矩阵

        既然全局地图状态向量包含所有局部子图特征、起始位姿、终止位姿，那么局部子图插入算法则变为一个使用局部变量信息大尺度静态估计问题（每一个局部地图仅仅涉及邻近对象——指被其它某些子图共有的地图特征或者起始终点位姿）。当扩展信息滤波用来解决估计问题的时候，两个在同一个局部子图中的对象就会产生非零非对角信息矩阵，无论多少子图融合，由于子图尺寸有限，任何对象都邻近对象有联系。这导致一个精确的稀疏信息矩阵（类似于平滑构图SAM——Smoothing and Mapping）。

       因为所有子图的对象都包含在全局信息向量中，在处理子图插入过程中没有边缘情况，因此信息矩阵持续保持稀疏性，因为构图中大多数机器人坐标是非边缘的，全局状态向量的维度是远少于SAM 和 full SLAM的。

2.3SLSJF的连续性

       SLSJF算法不包含任何近似值，这可能导致估计器的非一致性。更多的是，SLSJF是一个基于子图的策略法，在多数情况下与EKF SLAM比较改善了一致性，黄守东的前一篇文章展示了SLSJF能够在大尺度地图上产生一致性地图。然而，当大回环下、线性处理后的一些情况也会存在非一致性。

       SLSJF中，机器人的起始终止位置都存在全局状态向量中，在EIF中也没有预测步骤，因此地图插入问题可以转化为求最小均方差问题，在有良好的稀疏信息矩阵通过使用多重迭代法融合每一个子图将是一个更加精确解决方法。

3I-SLSJF算法

        I-SLSJF的状态向量与SLSJF的是一样的，不同之处在于地图融合处理过程。

3.1 输入与输出

        I-SLSJF 的输入是一系列通过一些SLAM算法生成的局部子图，一个局部子图使用以下符号表示：

                                                                                 

       其中标记'L'是局部子图的标记号，是状态向量的估计：

       其中是相关的协方差矩阵，状态向量包含机器人最终位姿(r标示机器人)，和所有的局部特征位置,这写数据采用传统的EKF SLAM产生，当局部子图建立时候通过坐标定义局部子图坐标系，例如，机器人开始于局部子图坐标系原点。

        假设一个机器人在子图k构建完毕后立刻构建子图k+1，那么上一个子图的终止坐标就是这个子图的开始坐标。

        机器人的输出是一个全局地图，全局地图包括了所有特征位子，所有子图终点坐标。全局地图是以状态估计、信息向量、信息矩阵的形式发布。

3.2 全局地图的状态变量

       为了方便起见，全局地图的起点设定为局部图1的起点，当局部子图1-k插入全局地图后，全局状态变量称作，G表示全局地图，的表达式如下包含，各个局部子图中所有特征在全局地图中的位置以及当前子图在全局地图的位姿，一句话表述，第i个图中全局特征（不包括前面的i-1个子图特征）的全局位置加上终点坐标的全局位姿，假设对于，现在插入k+1子图，该子图中有但是全局子图中没有的特征 加上终点坐标添加入全局变量，则变为

3.3 以最小均方差的方式进行局部地图融合

       假设局部地图j以表示，因为局部地图提供了相对起点的一致特征位置和终点位置，这个地图可以作为一个带有0期望的高斯噪声协方差矩阵为的激光观测值。

        为了描述清除，设局部子图j起始坐标，终点坐标,特征，。将终点坐标与特征减去起点坐标，再进行cos，sin转换为坐标值，再加上协方差为的0期望高斯噪声的wj，即可得到估计，因此融合局部子图1tok的方法是使用所有子图(1-k)的状态估计进行处理估计全局状态，这个问题可以化为最小二乘：

                               

                      是相对位置向量，如下：

                                  

     最小二乘公式：

                              

      最小方差问题可以使用线性化解决，实际上，在有旧的状态估计情况下，使用下面的线性化公式可以用来计算新的状态估计：

                                

       是函数Hj的雅克比矩阵，

                                      

            这个公式称为信息矩阵，它也是稀疏矩阵。          

       与SLSJF一样，I-SLSJF按照顺序融合子图进全局地图，规则类似于[Tardos et al.,2002][Williams,2001]，算法结构如下：

        1.将局部地图1号，作为全局地图；

        2.从2-p地图序号循环融合全局地图；

        3.结束。

3.4 数据联想

        数据联想这里是关于寻找k+1地图特征（已经包含在全局地图中），这里与SLSJF（Huang et al，2008）展现的一样，当估计错误过大，一些局部定位技术[Oaz et al.,2005]很有必要用来找到局部地图与全局地图匹配之处。

        1.数据关联

        2.使用EIF 初始化

        3.使用EIF 更新

        4.必要时，使用最小均方差进行优化

3.5使用EIF初始化