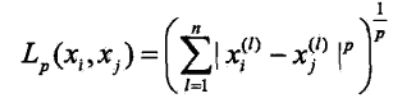《统计学习方法》—— 3.K近邻法(Python实现)
本文主要是在阅读过程中对本书的一些概念摘录,包括一些个人的理解,主要是思想理解不涉及到复杂的公式推导。若有不准确的地方,欢迎留言指正交流
本文完整代码见 github:https://github.com/anlongstory/awsome-ML-DL-leaning/lihang-reading_notes (欢迎 Star )
KNN (KNN.py)
K 近邻法( k-nearest neighbor, K-NN) 是一种基本的分类与回归方法,本文只探讨分类问题。
K 近邻法的定义为: 与之最近邻的 K 个实例,多数属于某一个类,则就判为这个类。 当 k =1 时,就是最近邻算法。
三个基本要素:
K值选择 + 距离度量 + 分类决策
当训练集,距离度量,k 值及分类决策规则确定后,其结果唯一。
K 值选择
k 值对 K 近邻法的结果影响很大。
- 如果 k 值较小,在较小的邻域进行训练和预测,近似误差会减小,学习的估计误差会增大。 k 值减小意味着整体模型变得复杂,容易发生过拟合。
- 如果 k 值较大,近似误差会增大,学习的估计误差会减小。K值增大意味着整体模型变得简单。
一般应用中 k 取一个比较小的值,然后采用交叉验证法来选取最优的 k 值。
距离度量
这里 p >=1 ,p=2 时,称为欧式距离, p=1时,称为曼哈顿距离,p = ∞ 就是各个坐标距离的最大值。
不同的距离度量,最近邻点是不同的。
代码示例 (L_distance.py):
import math
def L_distance(x,y,p):
sum = 0
for i in range (len(x)):
sum += math.pow(abs(x[i]-y[i]),p)
return math.pow(sum,1/p)
#demo 例 3.1
x=[1,1]
y=[4,4]
print(L_distance(x,y,1)) #
print(L_distance(x,y,2))
print(L_distance(x,y,3))
输出为:
6.0
4.242640687119285
3.7797631496846193
分类决策
K 近邻法中的分类决策就是多数表决,由输入实例的 k 个邻近的训练实例的多数类决定输入实例的类。误分类率为:
要是误分类率最下即经验风险最小,等价于多数表决规则。
最后代码运行结果可以
KNN代码实现(KNN.py)
def predict(self,x):
# 取出 n 个点
knn_list = []
for i in range(self.k): # 首先取前三个点加入列表中
dist = np.linalg.norm( x-self.X_train[i],ord=self.p)
knn_list.append((dist,self.y_train[i]))
for i in range(self.k , len(self.X_train)): # 然后将余下的点依次与列表中的点距离比较,有更小的则替换
max_index = knn_list.index(max(knn_list,key=lambda x:x[0])) # 按x[0]即 dist 来找最大值所在索引
dist = np.linalg.norm(x - self.X_train[i],ord=self.p) # 求范数
if knn_list[max_index][0] > dist: # 如果距离更近,就将当前最大值替换
knn_list[max_index] = (dist,y_train[i])
# 统计
knn =[k[-1] for k in knn_list] # 将最后 K 个点的分类结果新建一个列表
count_pairs = Counter(knn) # 计算每一个类别分别有几个
max_count = sorted(count_pairs)[-1] # 将出现次数由小到大排列,取最大的
return max_count
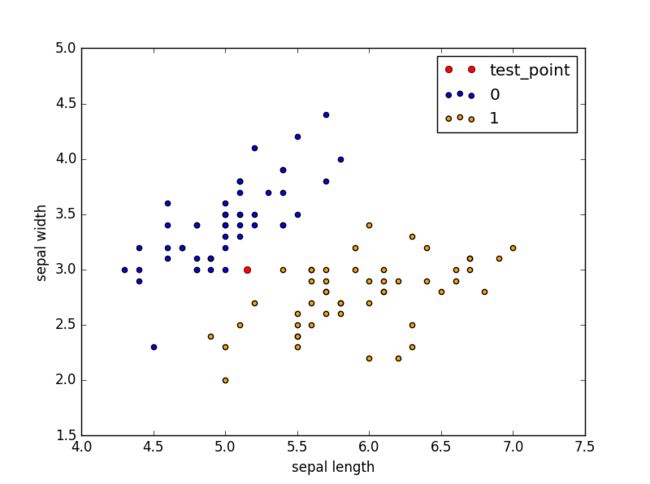
在 iris 数据集上,KNN.py 完整代码运行出来结果为:
> The result of classification: 1.0 #### kd 树 ( Kd-tree.py)k 最近邻法实现需要考虑如何快速搜索 k 个最近邻点。于是使用 kd 树来进行数据划分, kd 树是二叉树,表示对 k 维空间的一个划分,其每个结点对应于 K维空间划分中的一个超矩形区域。
构建kd树:
class KdTree(object):
def __init__(self,data):
k = len(data[0]) # 数据维度
def CreateNode(split, data_set): # 按第 split 维划分数据集创建 KdNode
if not data_set: # 如果数据为空,即到叶节点
return None
data_set.sort(key=lambda x:x[split]) # 在 x[split] 这个维度上由小到大的排序
split_pos = len(data_set) // 2 # 中位数位置
median = data_set[split_pos]
split_next = (split +1) % k # 改变维度,
# 递归的创建 kd 树
return KdNode(median,split,
CreateNode(split_next,data_set[:split_pos]), # 创建左子树
CreateNode(split_next,data_set[split_pos+1:])) # 创建右子树
self.root = CreateNode(0, data) # kd 树的根节点
kd 树的最近邻算法:
(1) 在 kd 树中依次遍历,通过对应维度上的数值大小来选择目标点该移动到左子树还是右子树,直到移动到 kd 树的叶节点。
def travel (kd_node,target,max_dist):
if kd_node is None:
return result([0]*k,float('inf'),0) # python中用float("inf")和float("-inf")表示正负无穷
nodes_visitd =1
s = kd_node.split # 进行维度分割,在构造 kd 树时,每个节点的分割维度已经通过计算定义好了
pivot = kd_node.dom_elt # 分割的点
if target[s] <= pivot[s]: # 如果在 s 维度目标值小于当前分割点的值
nearer_node = kd_node.left # 则目标最可能会出现在左子树中
further_node = kd_node.right
else:
nearer_node = kd_node.right # 反之目标会最可能出现在右子树中
further_node = kd_node.left
temp = travel(nearer_node,target,max_dist) # 进行遍历最可能包含目标点的子树区域
(2)以此叶节点为“当前最近点”
nearest = temp.nearest_point # 此叶节点作为 当前最近点
dist = temp.nearest_dist # 更新最近距离
(3)递归地向上回退,对每个节点进行如下操作:
a. 如果该节点保存的实例点比当前最近邻点离目标点近,则设此节点为最近邻点;
b. 当前最近点一定存在于该节点一个子节点对应的区域,检查当前最近邻点另一个子节点对应的区域是否有与目标点为球心、以目标点与当前最近邻的距离为半径的超球体相交;
c. 如果相交则在另一个子节点对应区域搜索是否存在比当前最近邻点更近的点,如果不相交直接返回,向上回退。
# 运行下面的部分说明找到比当前最近邻点还要近的点,更新相关信息
temp_dist = sqrt(sum((p1 - p2)**2 for p1,p2 in zip(pivot,target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近点
dist = temp_dist # 更新最近距离
max_dist = dist # 更新超球体半径
# 检查另一个子结点对应的区域是否有更近的点
temp2 = travel(further_node,target,max_dist)
nodes_visitd+=temp2.nodes_visited # 如果另一个子结点内存在更近距离
if temp2.nearest_dist < dist: # 更新最近点
dist = temp2.nearest_dist # 更新最近距离
return result(nearest,dist,nodes_visitd)
(4)当回退到根节点时,搜索结束,最后的最近邻点就是 x 的最近邻点
在例3.2的数据上给定目标点 [3,4.5],运行 Kd-tree.py 结果为:
Result_tuple(nearest_point=[5, 4], nearest_dist=1.8027756377319946, nodes_visited=4)
新建40万个3维的目标点,寻找其中目标点[0.1,0.5,0.8]的最近邻点结果为:
time: 6.44793839113302 s
Result_tuple(nearest_point=[0.100607809851333, 0.5014523470377854, 0.7918905810201691], nearest_dist=0.008260836575310295, nodes_visited=60)
相关阅读:
《统计学习方法》—— 1. 统计学习方法概论(Python实现)
《统计学习方法》—— 2. 感知器(Python实现)
《统计学习方法》—— 4. 朴素贝叶斯(Python实现)
《统计学习方法》—— 5. 决策树(Python实现)
《统计学习方法》—— 6. 逻辑斯特回归与最大熵模型(Python实现)
《统计学习方法》—— 7. 支持向量机(Python实现)
《统计学习方法》—— 8. 提升方法 (Python实现)
《统计学习方法》—— 9. EM 算法(Python实现)
《统计学习方法》——10. 隐马尔可夫模型(Python实现)
《统计学习方法》—— 11. 条件随机场