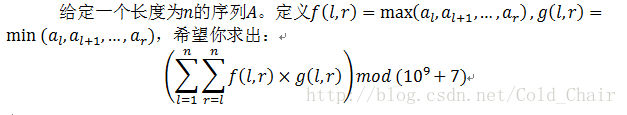【NOIP2017模拟A组模拟8.5】序列问题

Description：

1<=n<=500000

题解：

这种题马上想到的就是分治。

对于区间[x..y],将它分成三部分：
m = (x +ｙ)／２
1.左右端点都在[x..m]里的。
2.左右端点都在[m + 1..y]里的。
3.左右端点在m的两旁。

前两个递归处理，考虑第三个怎么求，这是分治的常规套路。

先考虑区间[m + 1..y]（右区间），以m+1为左端点，从左往右枚举右端点，min值会不断变小，max值会不断变大，将变化的地方存下来，分别放进两个数组里，设为a,b。

现在还要考虑区间[x..m]（左区间），从m出发，从右往左枚举左端点l，记录下min值和max值，设为min_l,max_l。

最后需要将两个区间合并。

在a数组里找到代表的值第一个小于min_l的位置u（从左往右看），
在b数组里找到代表的值第一个大于max_l的位置v（从左往右看）。
这个可以二分。
由于min_l不断缩小，max_r不断变大，也可以直接维护个指针。

右端点r的取法接下来有四种情况：

1.r < min(u, v)，min_[l..r] = min_l, min_[l..r] = min_r。

2.r >= max(u, v), min_[l..r] = [l..r]里的点到m+1的最小值，max_[l..r] = [l..r]里的点到m+1的最大值。

3..u <= v, u<=r < v,min_[l..r] = [l..r]里的点到m+1的最小值，max_[l..r] = min_r。

4.u >ｖ, v<=r < u,min_[l..r] = min_l,max_[l..r] = [l..r]里的点到m+1的最大值。

1可以直接算。
2、3、4维护前缀和就行了。

Code：

#include
#include
#define ll long long
#define fo(i, x, y) for(ll i = x; i <= y; i ++)
#define fd(i, x, y) for(ll i = x; i >= y; i --)
#define min(a, b) ((a) < (b) ? (a) : (b))
#define max(a, b) ((a) > (b) ? (a) : (b))
using namespace std;

const ll N = 500005, mo = 1e9 + 7;

ll n, a[N], u[N], v[N], s1[N], s2[N], s3[N];
ll ans;

void dg(ll x, ll y) {
    if(x > y) return;
    if(x == y) {
        ans = (ans + a[x] * a[x] % mo) % mo; 
        return;
    }
    ll m = (x + y) / 2;
    dg(x, m); dg(m + 1, y);
    u[0] = v[0] = 1;
    u[1] = v[1] = m + 1;
    s1[m] = s2[m] = s3[m] = 0;
    s1[m + 1] = a[m + 1];
    s2[m + 1] = a[m + 1];
    s3[m + 1] = a[m + 1] * a[m + 1];
    fo(i, m + 2, y) {
        if(a[i] < a[u[u[0]]]) u[++ u[0]] = i;
        if(a[i] > a[v[v[0]]]) v[++ v[0]] = i;
        s1[i] = (s1[i - 1] + a[u[u[0]]]) % mo;
        s2[i] = (s2[i - 1] + a[v[v[0]]]) % mo;
        s3[i] = (s3[i - 1] + a[u[u[0]]] * a[v[v[0]]]) % mo;
    }
    ll min = 1e9, max = -1e9, l = 1, r = 1;
    ll sum = ans;
    fd(i, m, x) {
        min = min(min, a[i]); max = max(max, a[i]);
        while(l <= u[0] && min <= a[u[l]]) l ++;
        while(r <= v[0] && max >= a[v[r]]) r ++;
        ll l1 = (l > u[0]) ? y : (u[l] - 1), r1 = (r > v[0]) ? y : (v[r] - 1);
        if(min(l1, r1) > m)
            ans += (min(l1, r1) - m) * min % mo * max % mo;
        if(max(l1, r1) < y)
            ans += s3[y] - s3[max(l1, r1)];
        if(l1 <= r1)
            ans += (s1[r1] - s1[l1]) * max % mo; else
            ans +=  min * (s2[l1] - s2[r1]) % mo;
        ans = (ans % mo + mo) % mo;
    }
}
int main() {
    freopen("seq.in", "r", stdin);
    freopen("seq.out", "w", stdout);
    scanf("%lld", &n);
    fo(i, 1, n) scanf("%lld", &a[i]);
    dg(1, n);
    printf("%lld\n", ans);
}