多尺度熵---Understanding Multiscale Entropy

关于本博客的说明：本文为翻译文章，原文为 ‘Understanding Multiscale Entropy’ 由Narayan P Subramaniyam 发布在SAPIEN LABS，原文链接为https://sapienlabs.co/understanding-multiscale-entropy/

一、引言

多尺度熵（Multiscale entropy, MSE）将样本熵扩展到多个时间尺度，以便在时间尺度不确定时提供额外的观察视角。样本熵的问题在于它没有很好地考虑到时间序列中可能存在的不同时间尺度。为了计算不同时间尺度下信号的复杂性，Costa等人（2002,2005）提出了多尺度熵。有关样本熵的相关知识请参考之前写的一篇博文https://blog.csdn.net/Cratial/article/details/79742363

与其他熵测量方法一样，多尺度熵的目标是评估时间序列的复杂性。使用多尺度熵的主要原因之一是不知道时间序列中相关的时间尺度。例如，在分析语音信号时，在单词时间尺度下统计信号的复杂度会比统计整个语音片段的复杂度更加有效。但如果你不知道音频信号代表语音，甚至对语音概念没有任何了解，你就不知道应该运用什么时间尺度以从原始信号中获得更多有用的信息。因此，通过多个时间尺度来分析问题将会得到更多信息。在脑电图中，潜在的脑电模式是未知的，因此相关的时间尺度也是未知的。所以，需要通过多尺度样本熵来分析哪个尺度对特定场合下脑电信号的分析更有用.

二、计算多尺度熵

多尺度熵的基本原理包括对时间序列进行粗粒化或下采样 - 主要是在越来越粗略的时间分辨率下分析时间序列。具体操作如下：

假设有以采样频率为1kHz采样得到的时间序列(原始时间尺度T为1 ms)

$$x_1，x_2，x_3，...... x_N$$

粗粒化（ Coarse Graining）数据意味着对不同数量的连续点取平均值，以创建不同尺度（或分辨率）的信号.

1. 当scale为1时，粗粒化数据的结果就是原始时间序列.

2. 当scale为2时，粗粒化后的时间序列是通过计算两个连续时间点的平均值形成的，如下图(A)所示。即定义y1 = (x1 + x2)/2; y2 = (x3 + x4)/2，以此类推.

3. 当scale为3时，粗粒化时间序列为三个连续时间点的平均值构成，如下图(B)所示。即定义y1 = (x1 + x2 + x3)/3; y2 = (x4 + x5 + x6)/3，依此类推.

图示来自文献[1].

粗粒化过程分为两种形式：一是非重叠式，每次跳跃τ个数据，取τ个数据做平均以产生新的数据；二是重叠式，每次跳跃1-τ个数据，取τ个数据做平均。

上述粗粒化过程为非重叠式，其数学定义为

其中，τ表示时间尺度.

然后，计算与每个尺度或分辨率对应的样本熵，并绘制样本熵－尺度曲线图。曲线下的面积是所选尺度范围内样本熵值之和，是多尺度熵的度量。一个波动较大的时间序列会产生较大的熵值，因此可以认为是具有较高复杂度的信号。同样，具有高度规律性的信号，其熵值也较低。

三、代码实现

备注：示例程序来自Björn Herrmann的个人网站上有关多尺度熵的介绍，原博文对四种不同噪声信号的多尺度熵进行了详细分析，说明了采用传统的样本熵进行分析可能存在的问题，源代码下载地址在此. 在此对Doctor Björn所做贡献表示感谢！

（为节省篇幅，此处仅给出了主程序，其中涉及的子函数请参见文末附录，或直接下载源代码.）

% matlab 主程序
clear all;
rand('seed',10)

%% generate signals
Sf  = 1000;  % Sampling frequency
dur = 30;  % Time duration
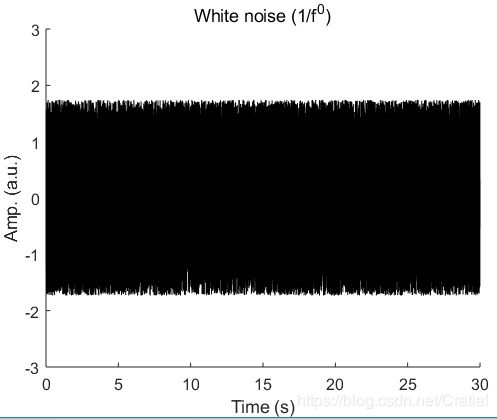
y = colored_noise(Sf,dur,0);  % white noise

%% Plot time course
t = (0:length(y)-1)/Sf;  % time vector
figure, set(gcf,'Color',[1 1 1]), hold on

set(gca,'FontSize',12)
plot(t,y,'-','Color',[0,0,0])
ylim([-3 3])
xlabel('Time (s)')
ylabel('Amp. (a.u.)')
title(['White' ' noise (1/f^{' num2str(0) '})'])

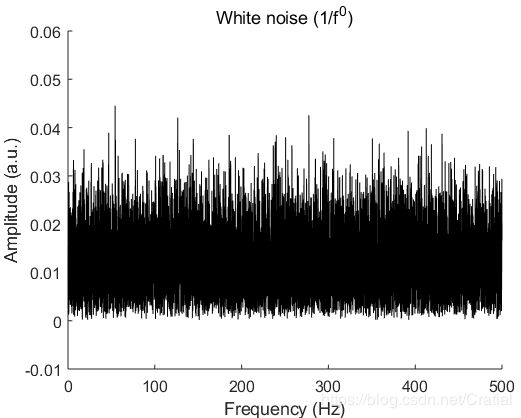
%% Plot spectra
[F xf] = spectra(y, Sf, Sf*10, @hann);
figure, set(gcf,'Color',[1 1 1]), hold on

set(gca,'FontSize',12)
plot(xf,abs(F),'-','Color',[0,0,0])
% xlim([0 400])
ylim([-0.01 0.06])
xlabel('Frequency (Hz)')
ylabel('Amplitude (a.u.)')
title(['White ' 'noise (1/f^{' num2str(0) '})'])

%% Compute MultiScale Entropy
% [mse sf] = MSE_Costa2005(x,nSf,m,r)
%
% x   - input signal vector (e.g., EEG signal or sound signal)
% nSf - number of scale factors
% m   - template length (epoch length); Costa used m = 2 throughout 
% r   - matching threshold; typically chosen to be between 10% and 20% of
%       the sample deviation of the time series; when x is z-transformed:
%       defined the tolerance as r times the standard deviation
%
% mse - multi-scale entropy
% sf  - scale factor corresponding to mse

[mse,sf] = MSE_Costa2005(y,20,2,std(y)*0.15);
    
%% Plot mse
figure, set(gcf,'Color',[1 1 1]), hold on, pp = []; labfull = {};
set(gca,'FontSize',12)
pp = plot(sf,mse,'-','Color',[0,0,0],'LineWidth',2);
labfull = ['White' ' noise (1/f^{' num2str(0) '})'];
ylim([0 3])
xlabel('Scale')
ylabel('SampEn')
title('Multi-scale entropy')
legend(pp,labfull)
legend('boxoff')

四、多尺度熵在脑电分析中的应用

由于MSE计算不同时间尺度下信号的熵，因此对于理解像EEG等生物信号在不同时间尺度下的复杂度变化十分有用. 熵与时间尺度的曲线可能会产生一个峰值，表明在该时间尺度下存在最大熵，该时间尺度可能具有更大的相关性。

事实上，Escudero等人[2]的研究表明，即使在10个电极的大时间尺度上，MSE也能发现阿尔茨海默症患者和对照组之间的显著差异，而且与对照组相比，阿尔茨海默症患者的脑电图活动没有那么复杂.

在Partk等人[3]的另一项研究中，他们对正常受试者（Normal）、阿尔茨海默病患者（Severe AD）和轻度认知障碍(MCI)患者的脑电信号进行了MSE分析。结果再次显示，阿尔茨海默病(AD)患者脑电信号的复杂性降低，其熵值较低，如图所示。正常和MCI被试在尺度为6、7时具有局部最大熵值，之后熵值下降。他们的分析还表明，在时间尺度因子为1时，轻度认知障碍、阿尔茨海默病和正常受试者的样本熵在统计学上是无法区分的，因此，在这种情况下，样本熵或近似熵等熵指标无法区分健康受试者和病理受试者.

在另一项研究中，Catarino等人[4]对健康受试者和自闭症谱系障碍(ASD)患者在执行社交和非社交任务(包括面部和椅子构成的视觉刺激)时的脑电信号进行了MSE分析。他们的结果显示，在枕叶和顶叶区域，与对照组相比，自闭症组的脑电图复杂性显著下降(p值统计结果).

图片来自文献[4]

因此，尽管以非特异性的方式，各种疾病状态都体现为MSE测量值下降。

MSE中的参数

MSE只是简单地将样本熵度量扩展到不同的时间尺度，因此，基础参数m(比较的线段长度)和r(两个线段之间的距离度量)是相同的。在前面的博客文章中讨论过，这些参数对于MSE的性能非常重要。关于如何选择这些参数，并没有标准的指导准则。对于数据长度m, 研究表明在MSE应用中，需要保证每个时间尺度下有足够的数据量。Costa等人[5]的研究表明，当白噪声和 1/f 噪声的数据点减少时，样本熵的均值(超过30个尺度)会发散。特别是在 1/f 噪声情况下，由于其非平稳性，与白噪声相比，发散速度更快。要查看参数m，r和数据长度对样本熵的影响，请参阅我们之前的博客文章以及Costa等人关于这些问题的另一篇优秀文章[5].

关于r，需要记住的是，为了避免噪声对样本熵估计的显著贡献，r必须大于大部分的信号噪声。选择r的另一个标准是基于信号的动态特性（signal dynamics）。

然而，最重要的方面是计算r的方式，以及所选择的距离测量（通常是欧几里德距离）是否真正与时间序列相关。例如，对于语音信号，欧几里德距离可能不是两个单词之间距离的最精确度量。脑电图完全有可能也是这种情况。

参考文献

[1] Busa, Michael A., and Richard EA van Emmerik. “Multiscale entropy: A tool for understanding the complexity of postural control.” Journal of Sport and Health Science 5.1 (2016): 44-51.

[2]  Escudero, J., et al. “Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy.” Physiological measurement 27.11 (2006): 1091.

[3] Park, Jeong-Hyeon, et al. “Multiscale entropy analysis of EEG from patients under different pathological conditions.” Fractals15.04 (2007): 399-404.

[4] Catarino, Ana, et al. “Atypical EEG complexity in autism spectrum conditions: a multiscale entropy analysis.” Clinical neurophysiology 122.12 (2011): 2375-2383.

[5] Costa, Madalena, Ary L. Goldberger, and C-K. Peng. “Multiscale entropy analysis of biological signals.” Physical review E 71.2 (2005): 021906.

附录

colored_noise.m

function [y] = colored_noise(Sf,dur,b)

% [y] = colored_noise(Sf,dur,b)
%
% Sf  - sampling frequency
% dur - duration
% b   - exponent of the 1/f^b power law function
%       b = 0 (white), 1 (pink), 2 (brown), -1 (blue), -2 (violet)
%
% y - noise time domain signal
%     (y is normalized such that mean(y)==0 and std(y)==1)
%
% Description: The script calculates a colored noise.
%
% ---------
%
%    Copyright (C) 2015
%    This program is free software: you can redistribute it and/or modify
%    it under the terms of the GNU General Public License as published by
%    the Free Software Foundation, either version 3 of the License, or
%    (at your option) any later version.
%
%    This program is distributed in the hope that it will be useful,
%    but WITHOUT ANY WARRANTY; without even the implied warranty of
%    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%    GNU General Public License for more details.
%
%    You should have received a copy of the GNU General Public License
%    along with this program.  If not, see .
%
% -----------------------------------------------------------------------
% B. Herrmann, Email: [email protected], 2015-08-27

% get number of samples
N = round(Sf * dur);
if mod(N,2)
    M = N + 1;
else
    M = N;
end

% get fourier spectrum and the corresponding frequency axis
F  = fft(rand([M 1]));
xf = (0:M/2-1)*(Sf/M);

% power law function
p = 1./xf(2:end).^b;

% get scaled magnitudes and phase
R = sqrt((abs(F(2:length(xf))).^2).*p');
P = angle(F(2:length(xf)));
	
% get symmetrical spectrum
F(2:length(xf))     = R .* (cos(P) + 1i.*sin(P));
F(length(xf)+2:end) = real(F(length(xf):-1:2)) - 1i*imag(F(length(xf):-1:2));

% IFFT
y = ifft(F);

% get correct number of samples
y = real(y(1:N));

% ensure unity standard deviation and zero mean value
y    = y - mean(y);
yrms = sqrt(mean(y.^2));
y    = y / yrms;

spectra.m

function [F xf] = spectra(X, Sf, nfft, win)

% [F xf] = spectra(X, Sf, nfft, win)
%
% Obligatory inputs:
%	X  - signal matrix (fft is done along the first dimension)
%	Sf - sampling frequency
%
% Optional inputs (defaults):
%	nfft = size(X,1); % length of samples in FFT (can be used for zero-padding)
%	win  = @hann; % @blackmanharris, @rectwin, @hann, @hamming, @blackman % window function applied to the data
%
% Outputs:
%	F  - fourier spectrum (amplitude normalized to reflect time domain units)
%	xf - x-axis for power/amplitude spectrum
%
% Description: The program computes the fouier spectrum along the first 
% dimension of a given matrix X. Gives only one half of the spectrum.
%
% References:
% van Drongelen W (2007) Signal processing for neuroscientists:
%	Introduction to the analysis of physiological signals. Amsterdam and
%	others: Academic Press.
%
% For infos on windowing see also: http://zone.ni.com/devzone/cda/tut/p/id/4844
%
% ---------
%
%    Copyright (C) 2012, B. Herrmann, M. Henry
%    This program is free software: you can redistribute it and/or modify
%    it under the terms of the GNU General Public License as published by
%    the Free Software Foundation, either version 3 of the License, or
%    (at your option) any later version.
%
%    This program is distributed in the hope that it will be useful,
%    but WITHOUT ANY WARRANTY; without even the implied warranty of
%    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%    GNU General Public License for more details.
%
%    You should have received a copy of the GNU General Public License
%    along with this program.  If not, see .
%
% -----------------------------------------------------------------------
% B. Herrmann, M. Henry, Email: [email protected], 2012-02-02

% check inputs
if nargin < 2, error('Error: Wrong number of inputs!\n'); end;
if nargin < 3 || isempty(nfft), nfft = size(X,1); end;
if nargin < 4 || isempty(win),  win = @hann; end;
if nfft < size(X,1); fprintf('Info: nfft < size(X,1)! Using nfft = size(X,1).\n'); nfft = size(X,1); end;

% reshape multidimensional data into 2-d matrix
siz = size(X);
n = siz(1); nrest = siz(2:end);
X = reshape(X,[n prod(nrest)]);

% get window function and multiply it with the data
xwin = window(win,n);
X = bsxfun(@times,X,xwin);

% compute FFT, F - complex numbers, fourier matrix
F = fft(X,nfft,1)*2/sum(xwin);

% get frequency axis
xf = (0:nfft/2)*(Sf/nfft);

% shorten matrix by half
F = F(1:length(xf),:);

% put data back into multi-d matrix
F = reshape(F,[size(F,1) nrest]);

MSE_Costa2005.m

function [mse,sf] = MSE_Costa2005(x,nSf,m,r)
% [mse(:,ii) sf] = MSE_Costa2005(y(:,ii),20,2,std(y(:,ii))*0.15);

% [mse sf] = MSE_Costa2005(x,nSf,m,r)
%
% x   - input signal vector (e.g., EEG signal or sound signal)
% nSf - number of scale factors
% m   - template length (epoch length); Costa used m = 2 throughout 
% r   - matching threshold; typically chosen to be between 10% and 20% of
%       the sample deviation of the time series; when x is z-transformed:
%       defined the tolerance as r times the standard deviation
%
% mse - multi-scale entropy
% sf  - scale factor corresponding to mse
%
% Interpretation: Costa interprets higher values of entropy to reflect more
% information at this scale (less predictable when if random). For 1/f
% pretty constant across scales.
%
% References:
% Costa et al. (2002) Multiscale Entropy Analysis of Complex Physiologic
%    Time Series. PHYSICAL REVIEW LETTERS 89
% Costa et al. (2005) Multiscale entropy analysis of biological signals.
%    PHYSICAL REVIEW E 71, 021906.
%
% Requires: SampleEntropy.m
%
% Description: The script calculates multi-scale entropy using a
% coarse-graining approach.
%
% ---------
%
%    Copyright (C) 2017, B. Herrmann
%    This program is free software: you can redistribute it and/or modify
%    it under the terms of the GNU General Public License as published by
%    the Free Software Foundation, either version 3 of the License, or
%    (at your option) any later version.
%
%    This program is distributed in the hope that it will be useful,
%    but WITHOUT ANY WARRANTY; without even the implied warranty of
%    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%    GNU General Public License for more details.
%
%    You should have received a copy of the GNU General Public License
%    along with this program.  If not, see .
%
% ----------------------------------------------------------------------
% B. Herrmann, Email: [email protected], 2017-05-06

% pre-allocate mse vector
mse = zeros([1 nSf]);

% coarse-grain and calculate sample entropy for each scale factor
for ii = 1 : nSf
	% get filter weights
	f = ones([1 ii]);
	f = f/sum(f);

	% get coarse-grained time series (i.e., average data within non-overlapping time windows)
	y = filter(f,1,x);
	y = y(length(f):end);
	y = y(1:length(f):end);
	
	% calculate sample entropy
	mse(ii) = SampleEntropy(y,m,r,0);
end

% get sacle factors
sf = 1 : nSf;

SampleEntropy.m

function SampEn = SampleEntropy(x,m,r,sflag)

% SampEn = SampleEntropy(x,m,r,sflag)
%
% Obligatory inputs:
%	x - input signal vector (e.g., EEG signal or sound signal)
%
% Optional inputs (defaults):
%	m     = 2;   % template length (epoch length)
%	r     = 0.2; % matching threshold (default r=.2), when standardized: defined the tolerance as r times the standard deviation
%	sflag = 1;   % 1 - standardize signal (zero mean, std of one), 0 - no standarization
%
% Output:
%	SampEn - sample entropy estimate (for a sine tone of 1s (Fs=44100) and r=0.2, m=2, the program needed 3.3min)
%
% References:
% Richman JS, Moorman, JR (2000) Physiological time series analysis using approximate 
%	   entropy and sample entropy. Am J Physiol 278:H2039-H2049
% Abasolo D, Hornero R, Espino P, Alvarez D, Poza J (2006) Entropy analysis of the EEG
%	   background activity in Alzheimer抯 disease patients. Physioogical Measurement 27:241�253.
% Molina-Pico A, Cuesta-Frau D, Aboy M, Crespo C, Mir�-Mart韓ez P, Oltra-Crespo S (2011) Comparative
%	   study of approximate entropy and sample entropy robustness to spikes. Artificial Intelligence
% 	 in Medicine 53:97�106.
%
% The first reference introduces the method and provides all formulas. But see also these two references, 
% because they depict the formulas much clearer. If you need a standard error estimate have a look at (or the papers):
% http://www.physionet.org/physiotools/sampen/
%
% Description: The program calculates the sample entropy (SampEn) of a given signal. SampEn is the negative 
% logarithm of the conditional probability that two sequences similar for m points remain similar at the next
% point, where self-matches are not included in calculating the probability. Thus, a lower value of SampEn
% also indicates more self-similarity in the time series.
%
% ---------
%
%    Copyright (C) 2012, B. Herrmann
%    This program is free software: you can redistribute it and/or modify
%    it under the terms of the GNU General Public License as published by
%    the Free Software Foundation, either version 3 of the License, or
%    (at your option) any later version.
%
%    This program is distributed in the hope that it will be useful,
%    but WITHOUT ANY WARRANTY; without even the implied warranty of
%    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%    GNU General Public License for more details.
%
%    You should have received a copy of the GNU General Public License
%    along with this program.  If not, see .
%
% -----------------------------------------------------------------------------------------------------
% B. Herrmann, Email: [email protected], 2012-01-15

% check inputs
SampEn = [];
if nargin < 1 || isempty(x), fprintf('Error: x needs to be defined!\n'), return; end
if ~isvector(x), fprintf('Error: x needs to be a vector!\n'), return; end
if nargin < 2 || isempty(m), m = 2; end
if nargin < 3 || isempty(r), r = 0.2; end
if nargin < 4 || isempty(sflag), sflag = 1; end

% force x to be column vector
x = x(:);
N = length(x);

 % normalize/standardize x vector
if sflag > 0, x = (x - mean(x)) / std(x); end  

% obtain subsequences of the signal
Xam = zeros(N-m,m+1); Xbm = zeros(N-m,m);
for ii = 1 : N-m                   % although for N-m+1 subsequences could be extracted for m,
	Xam(ii,:) = x(ii:ii+m);          % in the Richman approach only N-m are considered as this gives the same length for m and m+1
	Xbm(ii,:) = x(ii:ii+m-1);
end

% obtain number of matches
B = zeros(1,N-m); A = zeros(1,N-m);
for ii = 1 : N-m
	% number of matches for m
	d = abs(bsxfun(@minus,Xbm((1:N-m)~=ii,:),Xbm(ii,:)));
 	B(ii) = sum(max(d,[],2) <= r);
 	
	% number of matches for m+1
	d = abs(bsxfun(@minus,Xam((1:N-m)~=ii,:),Xam(ii,:)));
 	A(ii) = sum(max(d,[],2) <= r);
end

% get probablities for two sequences to match
B  = 1/(N-m-1) * B;                  % mean number of matches for each subsequence for m
Bm = 1/(N-m) * sum(B);               % probability that two sequences will match for m points (mean of matches across subsequences)
A  = 1/(N-m-1) * A;                  % mean number of matches for each subsequence for m+1
Am = 1/(N-m) * sum(A);               % probability that two sequences will match for m+1 points (mean of matches across subsequences)

cp = Am/Bm;                          % conditional probability
SampEn = -log(cp);                   % sample entropy

关于样本熵的说明，此处在构建m维和m+1维相空间时，相空间序列Xam和Xbm的维度均为N-m，此处与笔者之前介绍的样本熵计算法不一样，所以二者计算的结果也存在差异，两种方法都没有问题，故在此说明。