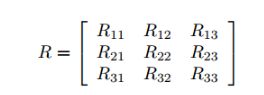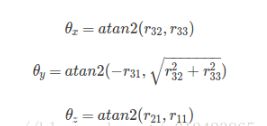欧拉角和旋转矩阵相互转换

（一）变换矩阵/F/H的svd分解或者旋转矩阵、平移矩阵求解

（二）欧拉角和旋转矩阵可同样表示刚体在三维空间的旋转，下面分享这两者互相转换的方法和核心代码

• 欧拉角转旋转矩阵 
  欧拉角通过将刚体绕过原点的轴(i,j,k)旋转θ，分解成三步，如下图（蓝色是起始坐标系，而红色的是旋转之后的坐标系）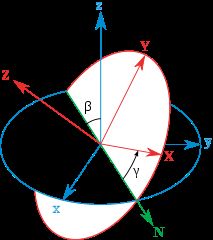 
   
  如果将每一个角度用旋转矩阵表示如下：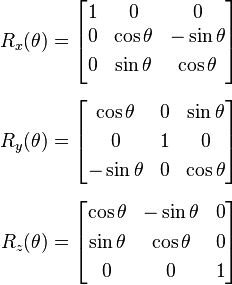 
   
  所以，容易得到，欧拉角转旋转矩阵如下：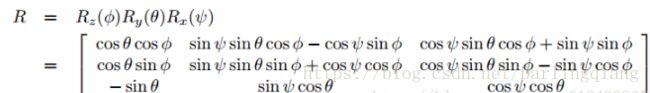 
• 
  

---

• 旋转矩阵转欧拉角 
  将旋转矩阵表示如下： 
•  
  则可以如下表示欧拉角： 
• 
  

---

代码

• 欧拉角转旋转矩阵

/**
欧拉角计算对应的旋转矩阵
**/
Mat eulerAnglesToRotationMatrix(Vec3f &theta)
{
    // 计算旋转矩阵的X分量
    Mat R_x = (Mat_(3,3) <<
               1,       0,              0,
               0,       cos(theta[0]),   -sin(theta[0]),
               0,       sin(theta[0]),   cos(theta[0])
               );


    // 计算旋转矩阵的Y分量
    Mat R_y = (Mat_(3,3) <<
               cos(theta[1]),    0,      sin(theta[1]),
               0,               1,      0,
               -sin(theta[1]),   0,      cos(theta[1])
               );


    // 计算旋转矩阵的Z分量
    Mat R_z = (Mat_(3,3) <<
               cos(theta[2]),    -sin(theta[2]),      0,
               sin(theta[2]),    cos(theta[2]),       0,
               0,               0,                  1);


    // 合并 
    Mat R = R_z * R_y * R_x;


    return R;
}

• 旋转矩阵转欧拉角

/*** 功能：  检查是否是旋转矩阵**/
bool isRotationMatrix(Mat &R)
{
    Mat Rt;
    transpose(R, Rt);
    Mat shouldBeIdentity = Rt * R;
    Mat I = Mat::eye(3,3, shouldBeIdentity.type());


    return  norm(I, shouldBeIdentity) < 1e-6;    
}

/**
 * 功能： 通过给定的旋转矩阵计算对应的欧拉角**/
Vec3f rotationMatrixToEulerAngles(Mat &R)
{
    assert(isRotationMatrix(R));


    float sy = sqrt(R.at(0,0) * R.at(0,0) +  R.at(1,0) * R.at(1,0) );


    bool singular = sy < 1e-6; // If


    float x, y, z;
    if (!singular) {
        x = atan2(R.at(2,1) , R.at(2,2));
        y = atan2(-R.at(2,0), sy);
        z = atan2(R.at(1,0), R.at(0,0));
    } else {
        x = atan2(-R.at(1,2), R.at(1,1));
        y = atan2(-R.at(2,0), sy);
        z = 0;
    }
    return Vec3f(x, y, z);   
}

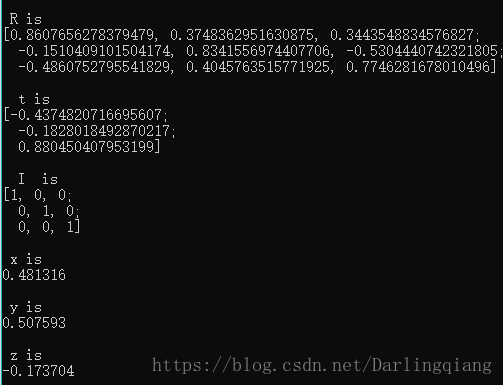
程序运行结果展示：

参考 
1. 欧拉角详解

暂做记录，后续补充