剑指offer题解（十一）：c++&java

序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树

1. 对于序列化：使用前序遍历，递归的将二叉树的值转化为字符，并且在每次二叉树的结点不为空时，在转化val所得的字符之后添加一个’ ， ‘作为分割。对于空节点则以 ‘#’ 代替。
   
   1. 对于反序列化：按照前序顺序，递归的使用字符串中的字符创建一个二叉树(特别注意：在递归时，递归函数的参数一定要是char ** ，这样才能保证每次递归后指向字符串的指针会随着递归的进行而移动！！！)

java

public class Solution {
    String Serialize(TreeNode root)
    {
        if(root==null)
            return "";
        StringBuilder sb = new StringBuilder();
        Serialize2(root,sb);
        return sb.toString();
    }
    void Serialize2(TreeNode root, StringBuilder sb)
    {
        if(root==null)
        {
            sb.append("#,");
            return;
        }
        sb.append(root.val);
        sb.append(',');
        Serialize2(root.left,sb);
        Serialize2(root.right,sb);
    }
    int index = -1;
    TreeNode Deserialize(String str)
    {
        if(str.length()==0)
            return null;

        String [] strs = str.split(",");
        return Deserialize2(strs);


    }

    TreeNode Deserialize2(String[] strs)
    {
        index++;
        if(!strs[index].equals("#"))
        {
            TreeNode root = new TreeNode(0);
            root.val = Integer.parseInt(strs[index]);
            root.left = Deserialize2(strs);
            root.right = Deserialize2(strs);
            return root;
        }
        return null;
    }
}

c++

class Solution {
public:
    vector<int> buf;
    void dfs1(TreeNode *root) {
        if(!root) buf.push_back(0xFFFFFFFF);
        else {
            buf.push_back(root->val);
            dfs1(root->left);
            dfs1(root->right);
        }
    }
    TreeNode* dfs2(int* &p) {
        if(*p==0xFFFFFFFF) {
            p++;
            return NULL;
        }
        TreeNode* res=new TreeNode(*p);
        p++;
        res->left=dfs2(p);
        res->right=dfs2(p);
        return res;
    }
    char* Serialize(TreeNode *root) {
        buf.clear();
        dfs1(root);
        int bufSize=buf.size();
        int *res=new int[bufSize];
        for(int i=0;ireturn (char*)res;
    }
    TreeNode* Deserialize(char *str) {
        int *p=(int*)str;
        return dfs2(p);
    }
};

字符串的排列

题目描述

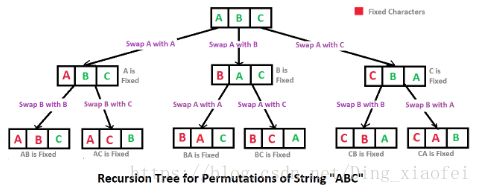
输入一个字符串，按字典序打印出该字符串中字符的所有排列。例如输入字符串 abc，则打印出由字符 a, b, c 所能排列出来的所有字符串 abc, acb, bac, bca, cab 和 cba。
ps:输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。

解题思路

c++

class Solution {
public:
    vector<string> Permutation(string str) {
        //可以用递归来做
        vector<string> array;
        if(str.size()==0)
            return array;
        Permutation(array, str, 0);
        sort(array.begin(), array.end());
        return array;
    }

    void Permutation(vector<string> &array, string str, int begin)//遍历第begin位的所有可能性
    {
        if(begin==str.size()-1)
            array.push_back(str);
        for(int i=begin; i<=str.size()-1;i++)
        {
            if(i!=begin && str[i]==str[begin])//有重复字符时，跳过
                continue;
            swap(str[i], str[begin]);//当i==begin时，也要遍历其后面的所有字符；
                                    //当i!=begin时，先交换，使第begin位取到不同的可能字符，再遍历后面的字符
            Permutation(array, str, begin+1);//遍历其后面的所有字符；

            swap(str[i], str[begin]);//为了防止重复的情况，还需要将begin处的元素重新换回来

            /*举例来说“abca”，为什么使用了两次swap函数
                交换时是a与b交换，遍历；
                交换时是a与c交换，遍历；（使用一次swap时，是b与c交换）
                交换时是a与a不交换；
                */
        }
    }
};

java

import java.util.*;

public class Solution {

    public ArrayList Permutation(String str) {
        ArrayList result = new ArrayList() ;
        if(str==null || str.length()==0) { return result ; }

        char[] chars = str.toCharArray() ;
        TreeSet temp = new TreeSet<>() ;
        Permutation(chars, 0, temp);
        result.addAll(temp) ;
        return result ;
    }

    public void Permutation(char[] chars, int begin, TreeSet result) {
        if(chars==null || chars.length==0 || begin<0 || begin>chars.length-1) { return ; }

        if(begin == chars.length-1) {
            result.add(String.valueOf(chars)) ;
        }else {
            for(int i=begin ; i<=chars.length-1 ; i++) {
                swap(chars, begin, i) ;

                Permutation(chars, begin+1, result);

                swap(chars, begin, i) ;
            }
        }
    }

    public void swap(char[] x, int a, int b) {
        char t = x[a];
        x[a] = x[b];
        x[b] = t;
    }

}

数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

解题思路

多数投票问题，可以利用 Boyer-Moore Majority Vote Algorithm 来解决这个问题，使得时间复杂度为 O(N)。

使用 cnt 来统计一个元素出现的次数，当遍历到的元素和统计元素不相等时，令 cnt–。如果前面查找了 i 个元素，且 cnt == 0 ，说明前 i 个元素没有 majority，或者有 majority，但是出现的次数少于 i / 2 ，因为如果多于 i / 2 的话 cnt 就一定不会为 0 。此时剩下的 n - i 个元素中，majority 的数目依然多于 (n - i) / 2，因此继续查找就能找出 majority。

java

public int MoreThanHalfNum_Solution(int[] nums) {
    int majority = nums[0];
    for (int i = 1, cnt = 1; i < nums.length; i++) {
        cnt = nums[i] == majority ? cnt + 1 : cnt - 1;
        if (cnt == 0) {
            majority = nums[i];
            cnt = 1;
        }
    }
    int cnt = 0;
    for (int val : nums)
        if (val == majority)
            cnt++;
    return cnt > nums.length / 2 ? majority : 0;
}

c++

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers)
    {
        if(numbers.empty()) return 0;

        // 遍历每个元素，并记录次数；若与前一个元素相同，则次数加1，否则次数减1
        int result = numbers[0];
        int times = 1; // 次数

        for(int i=1;iif(times == 0)
            {
                // 更新result的值为当前元素，并置次数为1
                result = numbers[i];
                times = 1;
            }
            else if(numbers[i] == result)
            {
                ++times; // 相同则加1
            }
            else
            {
                --times; // 不同则减1               
            }
        }

        // 判断result是否符合条件，即出现次数大于数组长度的一半
        times = 0;
        for(int i=0;iif(numbers[i] == result) ++times;
        }

        return (times > numbers.size()/2) ? result : 0;
    }
};

最小的 K 个数

题目描述

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

python

先皮一下

import heapq
class Solution:
    def GetLeastNumbers_Solution(self, tinput, k):
        if k> len(tinput):
            return []
        return list(heapq.nsmallest(k,tinput))

用api也可以通过相应的测试

解题思路

快速选择
复杂度：O(N) + O(1)
只有当允许修改数组元素时才可以使用
快速排序的 partition() 方法，会返回一个整数 j 使得 a[l..j-1] 小于等于 a[j]，且 a[j+1..h] 大于等于 a[j]，此时 a[j] 就是数组的第 j 大元素。可以利用这个特性找出数组的第 K 个元素，这种找第 K 个元素的算法称为快速选择算法。

public ArrayList GetLeastNumbers_Solution(int[] nums, int k) {
    ArrayList ret = new ArrayList<>();
    if (k > nums.length || k <= 0)
        return ret;
    int kthSmallest = findKthSmallest(nums, k - 1);
    // findKthSmallest 会改变数组，使得前 k 个数都是最小的 k 个数
    for (int i = 0; i < k; i++)
        ret.add(nums[i]);
    return ret;
}

public int findKthSmallest(int[] nums, int k) {
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int j = partition(nums, l, h);
        if (j == k)
            break;
        if (j > k)
            h = j - 1;
        else
            l = j + 1;
    }
    return nums[k];
}

private int partition(int[] nums, int l, int h) {
    // 切分元素
    int parti = nums[l];
    int i = l, j = h + 1;
    while (true) {
        while (i != h && nums[++i] < parti) ;
        while (j != l && nums[--j] > parti) ;
        if (i >= j)
            break;
        swap(nums, i, j);
    }
    swap(nums, l, j);
    return j;
}

private void swap(int[] nums, int i, int j) {
    int t = nums[i];
    nums[i] = nums[j];
    nums[j] = t;
}

最小堆的方法

复杂度：O(NlogK) + O(K)
特别适合处理海量数据
应该使用大顶堆来维护最小堆，而不能直接创建一个小顶堆并设置一个大小，企图让小顶堆中的元素都是最小元素。

维护一个大小为 K 的最小堆过程如下：在添加一个元素之后，如果大顶堆的大小大于 K，那么需要将大顶堆的堆顶元素去除。

public ArrayList GetLeastNumbers_Solution(int[] nums, int k) {
    if (k > nums.length || k <= 0)
        return new ArrayList<>();
    PriorityQueue maxHeap = new PriorityQueue<>((o1, o2) -> o2 - o1);
    for (int num : nums) {
        maxHeap.add(num);
        if (maxHeap.size() > k)
            maxHeap.poll();
    }
    ArrayList<Integer> ret = new ArrayList<>(maxHeap);
    return ret;
}