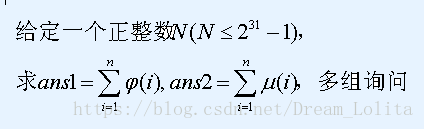【莫比乌斯反演-杜教筛练习】BZOJ3309 BZOJ3944 BZOJ4176
BZOJ3309 DZY Loves Math
【题目】
原题地址
对于正整数n,定义f(n)为n所含质因子的最大幂指数。例如f(1960)=f(2^3 * 5^1 * 7^2)=3, f(10007)=1, f(1)=0。
给定正整数a,b,求sigma(sigma(f(gcd(i,j)))) (i=1..a, j=1..b)。
【解题思路】
Ans=∑ad=1f(d)∑⌊ad⌋i=1∑⌊bd⌋j=1[(i,j)=1] A n s = ∑ d = 1 a f ( d ) ∑ i = 1 ⌊ a d ⌋ ∑ j = 1 ⌊ b d ⌋ [ ( i , j ) = 1 ]
Ans=∑ad=1f(d)∑⌊ad⌋d′=1μ(d′)⌊add′⌋⌊bdd′⌋ A n s = ∑ d = 1 a f ( d ) ∑ d ′ = 1 ⌊ a d ⌋ μ ( d ′ ) ⌊ a d d ′ ⌋ ⌊ b d d ′ ⌋
令 T=dd′ T = d d ′
Ans=∑aT=1⌊aT⌋⌊bT⌋∑d|Tf(d)∗mu(Td) A n s = ∑ T = 1 a ⌊ a T ⌋ ⌊ b T ⌋ ∑ d | T f ( d ) ∗ m u ( T d )
那么设 g[T]=∑d|Tf(d)∗mu(Td) g [ T ] = ∑ d | T f ( d ) ∗ m u ( T d )
接下来问题在于怎么求g。
以下摘自我忘记名字的大佬:
g数组的预处理看起来是带log的。但是根据莫比乌斯函数的性质,如果\frac T d存在平方因子,函数值是等于0的,也就是对答案没有贡献。
那么设 T=p1k1∗p2k2∗...∗pmkm T = p 1 k 1 ∗ p 2 k 2 ∗ . . . ∗ p m k m ,T质因数的最大幂是k,那么只有ki=k的质因数有用。又可以设 Td=p1a1∗p2a2∗...∗pmam T d = p 1 a 1 ∗ p 2 a 2 ∗ . . . ∗ p m a m ,其中ai∈[0,1]。
可以发现f(d)只能取到k,k-1,现在令其中一个满足ki=k的质因数为d的最大幂,如果f(d)=k,那么ai=0,其它为0或1均可。然而一个a取0,就相当于给莫比乌斯函数乘1,取1就是乘-1。所以最终答案乘的系数是0。特殊情况:如果T是质数,乘的系数是1(因为没有其它质因数了)。
如果f(d)=k-1,那么ai=1,所有其它满足ki=k的质因数也要让对应的a值取1,这时剩下的质因数也和上面一样,最后得到的系数是0。特殊情况:如果每个ki都等于k,那么由于没有剩下可以取0、1的质因数,它的系数也是1。
这样就可以线性预处理了。
以下摘自popoqqq:
观察这个函数 由于含平方因子数的μ值都为零,因此我们只考虑μ(T/d)!=0的数
令T=p1^a1*p2^a2*…pk^ak,d=p1^b1*p2^b2…*pk^bk
那么0<=(ai-bi)<=1
如果存在ai≠aj(i≠j),那么我们可以将所有的a分为两部分:最大的a的集合A和非最大a的集合B
很显然f值由A中的选取方案决定
对于A中的每种选取方案,μ值决定于总选择的数量的奇偶性
在集合B中选取奇数个元素和偶数个元素的方案数是相等的,故对于A中的每种选取方案,得到的和都是0
故如果存在ai≠aj(i≠j),则g(T)=0
反之,如果所有的a值都相等,我们假设对于任意选取方案,f值都不变
那么由于选取奇数个元素和偶数个元素的方案数相等,和仍然为0
但是有一种选取方案的f值=a-1 因此我们要将这个1减掉
考虑到μ的符号之后,最终结果为(-1)^(k+1)
故如果不存在ai≠aj,则g(T)=(-1)^(k+1)
嗯,这道题后面的柿子还是想不到。
#includeif(!bo[i])
pri[++pnum]=i,mu[i]=-1;
for(int j=1;j<=pnum && i*pri[j]*pri[j]]=1;
if(!(i%pri[j]))
{
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
}
}
for(int i=2;iif(mu[i])
for(LL j=i;j*=i)
s[j]=-mu[i];
for(int i=2;is[i]+=s[i-1];
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("BZOJ3309.in","r",stdin);
freopen("BZOJ3309.out","w",stdout);
#endif
init();
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&x,&y);ans=0;
if(x>y) swap(x,y);
for(int i=1,las;i<=x;i=las+1)
{
las=min(x/(x/i),y/(y/i));
ans+=(s[las]-s[i-1])*(x/i)*(y/i);
}
printf("%lld\n",ans);
}
return 0;
} BZOJ3944 SUM
【解题思路】
为了更快地求 F(i)=∑ni=1f(i) F ( i ) = ∑ i = 1 n f ( i ) ,我们构造一个函数 g(n) g ( n ) ,求出 (f∗g)(n) ( f ∗ g ) ( n ) 的前缀和。
∑ni=1(f∗g)(i)=∑ni=1∑d|if(d)g(id)=∑ij<=nf(i)g(j)=∑ni=1g(i)F(⌊ni⌋) ∑ i = 1 n ( f ∗ g ) ( i ) = ∑ i = 1 n ∑ d | i f ( d ) g ( i d ) = ∑ i j <= n f ( i ) g ( j ) = ∑ i = 1 n g ( i ) F ( ⌊ n i ⌋ )
所以 g(1)F(n)=∑ni=1(f∗g)(i)−∑ni=2g(i)F(⌊ni⌋) g ( 1 ) F ( n ) = ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ n i = 2 g ( i ) F ( ⌊ n i ⌋ )
于是我们的目标就是快速求出 ∑ni=1(f∗g)(i) ∑ i = 1 n ( f ∗ g ) ( i ) 和 g(i) g ( i ) 的前缀和。这样我们的复杂度就是 O(n34) O ( n 3 4 ) ,如果我们将 O(n23) O ( n 2 3 ) 以内的 F(i) F ( i ) 预处理,那么复杂度就可以降到 O(n23) O ( n 2 3 ) (复杂度怎么证。。)
g g 一般取恒等函数 I I 。
这里求 ∑ni=1μ(i) ∑ i = 1 n μ ( i ) 就是求 ∑ni=1∑d|iμ(d)−∑ni=2F(⌊ni⌋) ∑ i = 1 n ∑ d | i μ ( d ) − ∑ i = 2 n F ( ⌊ n i ⌋ )
则 Ans=1−∑ni=2F(⌊ni⌋) A n s = 1 − ∑ i = 2 n F ( ⌊ n i ⌋ )
求 ∑ni=1ϕ(i) ∑ i = 1 n ϕ ( i ) 就是求 ∑ni=1∑d|iϕ(d)−∑ni=2F(⌊ni⌋) ∑ i = 1 n ∑ d | i ϕ ( d ) − ∑ i = 2 n F ( ⌊ n i ⌋ )
则 Ans=n(n+1)2−∑ni=2F(⌊ni⌋) A n s = n ( n + 1 ) 2 − ∑ i = 2 n F ( ⌊ n i ⌋ )
然后后面的用map+记忆化搜索,同时先预处理出来前2000000左右的答案即可。
这个东西不能分开做,不然会T得飞起啊!
#include pii;
const int N=2000000;
int pnum;
int pri[N],bo[N];
LL phi[N],mu[N];
map<int,LL> P,M;
map<int,LL>::iterator it,it2;
void init()
{
phi[1]=mu[1]=1;
for(int i=2;iif(!bo[i])
pri[++pnum]=i,phi[i]=i-1,mu[i]=-1;
for(int j=1;j<=pnum && i*pri[j]1;
if(!(i%pri[j]))
{
phi[i*pri[j]]=phi[i]*pri[j];
mu[i*pri[j]]=0;
break;
}
phi[i*pri[j]]=phi[i]*(pri[j]-1);
mu[i*pri[j]]=-mu[i];
}
}
for(int i=2;i1],mu[i]+=mu[i-1];
}
pii calc(LL x)
{
if(xreturn mkp(phi[x],mu[x]);
it=P.find(x);it2=M.find(x);
if(it!=P.end()) return mkp(it->second,it2->second);
LL res1=x*(x+1)/2ll,res2=1;
for(LL i=2,las;i<=x;i=las+1)
{
las=x/(x/i);pii rt=calc(x/i);
res1-=(las-i+1)*rt.fi;
res2-=(las-i+1)*rt.se;
}
P[x]=res1;M[x]=res2;
return mkp(res1,res2);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("BZOJ3944.in","r",stdin);
freopen("BZOJ3944.out","w",stdout);
#endif
init();
int T,x;
scanf("%d",&T);
while(T--)
{
scanf("%d",&x);pii ans=calc(x);
printf("%lld %lld\n",ans.fi,ans.se);
}
return 0;
} BZOJ4176 Lucas的数论
【题目】
原题地址
【解题思路】
首先我们用上BZOJ3994推导出的结果:
f(nm)=∑i|n∑j|m[gcd(i,j)==1] f ( n m ) = ∑ i | n ∑ j | m [ g c d ( i , j ) == 1 ]
然后用这个柿子去反演:
∑nx=1∑ny=1f(xy) ∑ x = 1 n ∑ y = 1 n f ( x y )
∑nx=1∑ny=1∑i|x∑j|y[gcd(i,j)==1] ∑ x = 1 n ∑ y = 1 n ∑ i | x ∑ j | y [ g c d ( i , j ) == 1 ]
∑nx=1∑ny=1∑i|x∑j|y∑d|gcd(i,j)μ(d) ∑ x = 1 n ∑ y = 1 n ∑ i | x ∑ j | y ∑ d | g c d ( i , j ) μ ( d )
∑nd=1μ(d)∑⌊nd⌋x=1∑⌊nd⌋y=1∑⌊ndx⌋i=1∑⌊ndy⌋j=1 ∑ d = 1 n μ ( d ) ∑ x = 1 ⌊ n d ⌋ ∑ y = 1 ⌊ n d ⌋ ∑ i = 1 ⌊ n d x ⌋ ∑ j = 1 ⌊ n d y ⌋
∑nd=1μ(d)(∑⌊nd⌋i=1⌊ndi⌋)2 ∑ d = 1 n μ ( d ) ( ∑ i = 1 ⌊ n d ⌋ ⌊ n d i ⌋ ) 2
注意到 ⌊nd⌋ ⌊ n d ⌋ 只有 n−−√ n 种取值,可以枚举然后求前缀和,后面的sigma, ⌊ndi⌋ ⌊ n d i ⌋ 只有 O(n√d) O ( n d ) 种取值,就直接用这个复杂度求出。
因为 n n 比较大,所以还要用上杜教筛。
PS.注意取模
#includeif(!bo[i])
pri[++pnum]=i,mu[i]=-1;
for(int j=1;j<=pnum && i*pri[j]1;
if(!(i%pri[j]))
{
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
}
}
for(int i=2;i1];
}
LL calcmu(int x)
{
if(xreturn mu[x];
if(mp[x]) return mp[x];
LL res=1;
for(int i=2,las;i<=x;i=las+1)
{
las=x/(x/i);
res-=calcmu(x/i)*(las-i+1);
}
return mp[x]=res;
}
LL calc(int x)
{
LL res=0;
for(int i=1,las;i<=x;i=las+1)
{
las=x/(x/i);
(res+=((LL)(x/i)*(las-i+1))%mod)%=mod;
}
return res;
}
LL sqr(LL x)
{
return x*x%mod;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("BZOJ4176.in","r",stdin);
freopen("BZOJ4176.out","w",stdout);
#endif
init();scanf("%d",&n);
for(int i=1,las;i<=n;i=las+1)
{
las=n/(n/i);
(ans+=(LL)(calcmu(las)-calcmu(i-1)+mod)%mod*sqr(calc(n/i)%mod)%mod)%=mod;
}
printf("%lld\n",ans);
return 0;
} 【总结】
数论入门.jpg