MATLAB数字信号处理（1）四种经典功率谱估计方法比较

这是我研究生课程“现代信号处理”中的作业报告，上传到blog中。

---

经典功率谱估计

可以采用直接法，也称周期图法，利用公式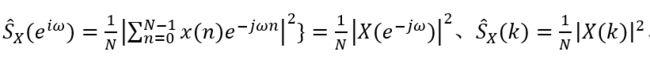计算功率谱密度。或者根据自相关函数和谱密度之间的傅里叶变换关系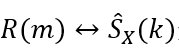
来计算，称为间接法或自相关函数法。

还可以先作加窗平滑处，对序列x(n)或估计的自相关函数进行加窗（如汉宁窗、汉明窗）截断，前者称作数据窗，后者称作滞后窗。

---

MATLAB编程实现

对信号x(n)=sin⁡(ωt)+n(t)和x(n)=exp⁡(jωt)+n(t)使用上述4种方法进行功率谱估计。叠加高斯白噪声n(t)后的信噪比为-10dB、-3dB、3dB、10dB四种情况。编程不使用fft、xcorr等MATLAB提供的函数。

关键程序如下，四个函数分别使用不同方法进行功率谱估计，一个函数用于绘图。调用自己编写的函数实现功能（MATLAB R2017a版本下测试）。

N = 512; fs = 1; M=256;
t = (0:N-1)/fs;
x1n = sin(2*pi*0.1*t);           %信号1，实信号
x2n = exp(1j*2*pi*0.1*t);      %信号2，复信号

P_estimation(x1n, 10, N, M, fs);    %估计不同SNR、不同信号的功率谱
P_estimation(x1n, 3, N, M, fs);      
P_estimation(x1n, -3, N, M, fs);    
P_estimation(x1n, -10, N, M, fs);    
P_estimation(x2n, 10, N, M, fs);    
P_estimation(x2n, 3, N, M, fs);    
P_estimation(x2n, -3, N, M, fs);   
P_estimation(x2n, -10, N, M, fs);    

%   对叠加SNR的信号xn，使用方法1-4进行功率谱估计
function P_estimation(xn, snr, N, M, fs)
    sn = awgn(xn, snr, 'measured');
    f1=(0:N-1)*fs/N;                        %功率谱坐标轴
    Sx1 = direct_method(sn, N);     % 方法1：直接法  
    Sx2 = indir_method(sn,N,M);    % 方法2：间接法  
    Sx3 = add_datawin(sn, N);        % 方法3：数据加窗 
    Sx4 = add_rxwin(sn,N,M);         % 方法4：自相关函数加窗
    figure;
    subplot(221); plot(f1,10*log10(Sx1));
    title('直接法 SNR='+string(snr)); xlabel('f/Hz'); ylabel('Sx(f)(dB/Hz)');
    subplot(222); plot(f1,10*log10(Sx2));
    title('间接法 SNR='+string(snr)); xlabel('f/Hz'); ylabel('Sx(f)(dB/Hz)');
    subplot(223); plot(f1,10*log10(Sx3));
    title('数据加窗 SNR='+string(snr)); xlabel('f/Hz'); ylabel('Sx(f)(dB/Hz)');
    subplot(224); plot(f1,10*log10(Sx4));
    title('自相关函数加窗 SNR='+string(snr)); xlabel('f/Hz'); ylabel('Sx(f)(dB/Hz)');    
end

%    方法1：直接法得到频率谱估计
function Sx = direct_method(xn, N)   %估计N点序列xn的功率谱Sx
    Sx = zeros(1,N);
    for index = 1 : N
        for n = 0 : N-1       %求Fourier变换
            Sx(index) = Sx(index) + xn(n+1)*exp(-1j*n*index*2*pi/N);  
        end
        Sx(index) = abs(Sx(index))*abs(Sx(index))/N;  %求功率谱
    end
end

%    方法2：间接法得到频率谱估计
function Sx = indir_method(xn,N,M)   %估计N点序列xn的功率谱Sx    
    Rx = zeros(1,2*M-1);   %M为估计的自相关函数的点数，1<

---

结果分析

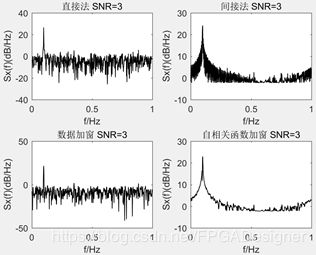
下面是不同信噪比下对x(n)=sin⁡(ωt)+n(t)信号的功率谱估计结果。




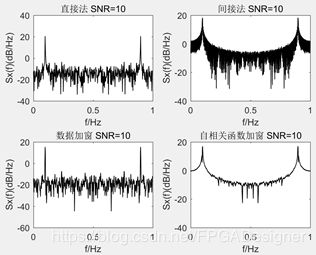
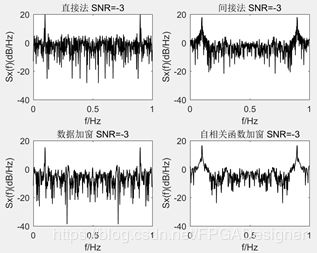
程序中采样频率为1，信号频率为0.1。实信号的功率谱是对称的，在图中可以看到两个尖峰在0.1和与之对称的0.9处。对于直接法而言，数据加窗后的“尖峰”更窄；对于间接法而言，自相关函数加窗后的功率谱图更平滑。这也是其称作“修正周期图”和“周期图平滑”的直观体验。

下面是不同信噪比下对x(n)=exp⁡(jωt)+n(t)信号的功率谱估计结果。




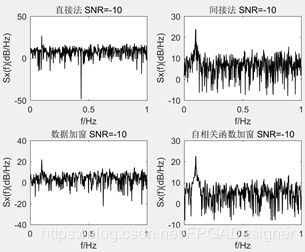
可以得到和上一组测试相同的结论。只不过复信号的功率谱不具有对称性。总体而言，信噪比越高，信号的功率峰也就越突出。

---

不同窗函数比较

下面给出直接法和间接法中，不加窗、汉明窗、汉宁窗、布莱克曼窗的差别。为了更直观地观察使用不同窗函数之间的区别，没有添加噪声。直接法中汉明窗将功率峰变得更窄；汉宁窗和布莱克曼窗效果类似，增大了功率峰值和其余功率值之间的倍数。

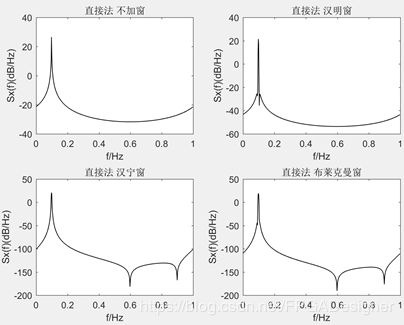
间接法中加三个窗函数都起到了周期图平滑的作用，汉宁窗和布莱克曼窗的平滑效果看起来比汉明窗要好一些。但三个窗函数都没有改变功率峰值和其余功率值之间的倍数关系。