【拓扑排序】（一）（poj2585）window pains

题目

window pains

知识

拓扑排序（TopologicalSort）算法：

时间之间按先后关系可以画成有向图。先后关系参见下图：

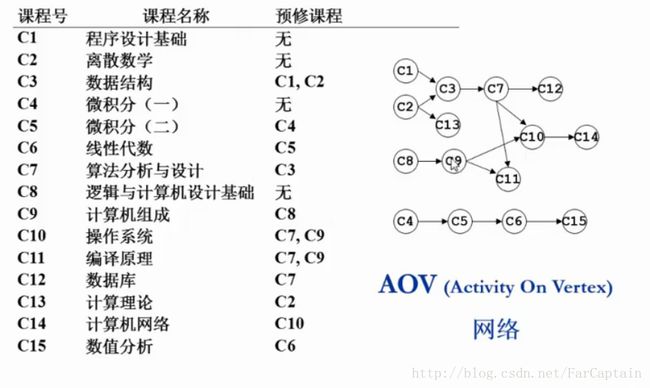
称为“AOV”（activity on vertex）网络，就是事件是由点描述的，边表示某种关系。（AOE“activity on edge”）
如上例，学校在排课时要形成若干种可能的合理顺序，这些顺序称为“拓扑序”。生成一种拓扑序称为“拓扑排序”。

可以形成拓扑序的AOV是：

• 连通的
• 无环的（因为如果有环路，那么先后顺序是交叉的，不再topo）

所以利用TopologicalSort 可以判定AOV是否DAG（Directed Acyclic Graph 有向无环图）；

思路

这道题不同窗口之间的覆盖关系，显然也是有向图中的“盖住”关系。（A盖住B <==> A——>B）;
因此每个窗口是一个事件，九个节点可以形成DAG，（就是该AOV可以形成完整topo），就是合理的覆盖情况。（题中“clean”的）。

算法

直接祭出伪码：

代码

初始化

我直接用笔画出来每个方格（4*4的小方格）可能出现的数字（有人用程序先算出来，不过这个是定值而且不麻烦，建议手画），存在三维数组tab里（前两个坐标是位置，第三个是可能元素）。

getGraph

简单粗暴地用矩阵存图。由于topoSort需要，维护一个出度数组。

topoSort（算法）

用一个stack做open表（queue也行，这里没关系）。

#include 
#include 
#include 
#include 

using namespace std;
int tab[4][4][4]={ {{1},{1,2},{2,3},{3}},
{{1,4},{1,2,4,5},{2,3,5,6},{3,6}},
{{4,7},{4,5,7,8},{5,6,8,9},{6,9}},
{{7},{7,8},{8,9},{9}} };///i,j位置上最多四个

int tabcnt[4][4]={{1,2,2,1},{2,4,4,2},{2,4,4,2},{1,2,2,1}};//i,j窗口数
bool G[9][9];//1~9九个节点
int indegree[9];//入度

bool topoSort()
{
    int cnt = 0;
    stack<int> st;

    for(int i=1;i<=9;i++)
        if(indegree[i-1]==0)st.push(i);

        while(!st.empty()){
            cnt++;
            int u = st.top();
            st.pop();
            for(int i=1;i<=9;i++)
                if(G[u-1][i-1]&&(--indegree[i-1]==0)){
                    st.push(i);
                }
        }

        //printf("%d\n",cnt);
    return cnt == 9;
}


int main()
{
    char buf[64];

    while(scanf("%s",buf)!=EOF){//undo of input
        if(strcmp(buf,"ENDOFINPUT")==0)break;
        memset(G,0,sizeof(G));
        memset(indegree,0,sizeof(indegree));

        int x;
        for(int i=0;i<4;i++)
            for(int j=0;j<4;j++){
                scanf("%d",&x);
                 //x-1 to be an index

                for(int k=0;k//getGraph
                    if(x != tab[i][j][k]){
                        ///G  x 盖住 tab[i][j][k]
                        if(G[x-1][ tab[i][j][k]-1 ]==0){
                            G[x-1][ tab[i][j][k]-1 ] = 1;
                            indegree[tab[i][j][k]-1]++;
                        }
                    }
            }

           printf("THESE WINDOWS ARE %s\n", topoSort() ? "CLEAN" : "BROKEN");


        scanf("%s",buf);
    }
    return 0;
}