对数据结构一点一小小的理解(四)——线性表
作为一位大三的学生,近期在复习《数据结构与算法》这本教材;以下是我对复习内容的一点小小的理解,只是个人的部分观点,如有错误给您带来不便请您谅解
线性表
什么是线性表呢?
是一种简单的线性结构(线性结构是一个数据元素的有序(次序)集)是一个有限的集合
线性结构特征
集合中必存在唯一的一个第一元素和最后元素,每个元素都有一个唯一的后继(通俗的来讲跟在我后面的只有一个),除了第一个元素之外,都有一个前驱
元素个数是线性表的长度,例如个数为n,即长度为n
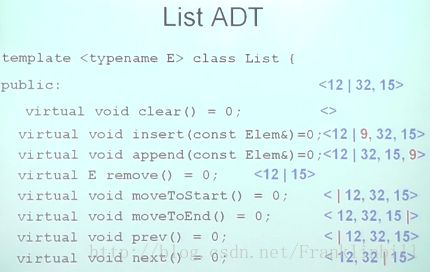
操作一般都是对当前元素来进行,常用的表示方法是<20,24|12,15>*当前元素即为* | 后的 12(即2号位的,0,1,2,2号位为12)
对上图的部分解释:
**clear() 清空(变成一个空表)
insert() 插入(在当前位置前面)
append() 追加(在最后位置加一个元素)
remove() 删除当前元素(当前位置还在那个地方)
movetostart() 把当前位置移到最开头
movetoend() 把当前位置移到最后面
prev() 把当前位置往前移一个位置
next() 把当前位置往后移一个位置
length() 线性表长度(线性表有几个元素)
currpos() 当前的位置
movetopos() 把当前位置移到xxxx
getvalue() 获取当前位置的值**
基于数组的线性表(用数组存储的线性表)
template <typename E>
class AList : public List {
private:
int maxSize;//数组最大是多大
int listSize;//当前真正存储的元素的个数是多少
int cure;//当前的元素
E* ListArray;//定义一个指针,用于初始化数组存储元素
public:
AList(int size = defaultSize){//构造函数
maxSize = size;
listSize = cure = 0;
listArray = new E[maxSize];//分配空间
}
~AList(){delete[] listArray;}//释放指针空间(防止内存泄漏)
}
//
void clear(){
delete[] listArray;
listSize = curr = 0;
listArray = new E[maxsize];
}
//
void moveToStart(){
cure = 0;
}
//
void moveToEnd(){
cure = listSize;
}
//
void prev(){
if(cur != 0)
curr--;
}
//
void next(){
if(curr < listSize)
curr++;
}
//
int length() const {
return listSize
}
元素插入部分代码
//insert "it" at current position
template <typename E>
void AList::insert(const E& it){
Assert(listSize < maxSize,"list capacity exceeded");
//shift Elems up to make room
for(int i = listSize ; i > cure ; i--)
listArray[i]=listArray[i-1];
listArray[curr] = it;
listSize++;//Increment list size
} 注意:元素搬家的时候需要采用递减的循环,递增的循环会出问题
分析一下他的时间复杂度:
平均移动元素的个数:假设在第i个元素前的概率为Pi,则在长度位n的线性表中插入一个元素需要移动的元素个数n-i+1
![]()
Append 追加
//Append elem to end of the list
template <typename E>
void AList::append(const E& it){
Assert(listSize"list capacity exceeded");
listArray[listSize++] = it;
} 删除操作
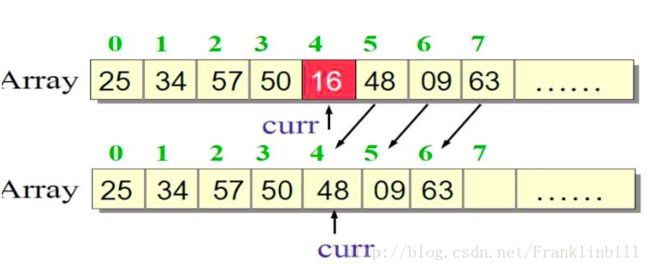
先看一个图例来了解一下:删除16这个位置,删除元素往前移,和插入相反
//remove and return current element
template <typename E>
List::remove(){
Assert((cur >= 0)&&(cur < list),"no element");
E it = listArray[curr];//copy elements
//shift them down
for(int i = curr; i < listSize-1; i++)
listArray[i] = listArray[i+1];
listSize--; //Decrement size
return it;
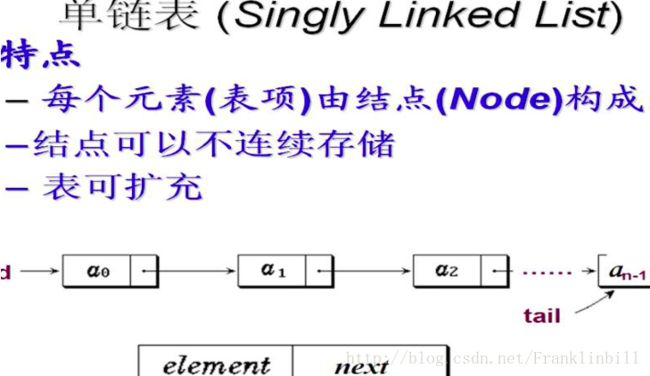
} 链式存储结构Linked list(链表)
两种链表:单链表(我只知道你的,你只知道你下一个的);双向链表(我知道你的,你也知道我的)
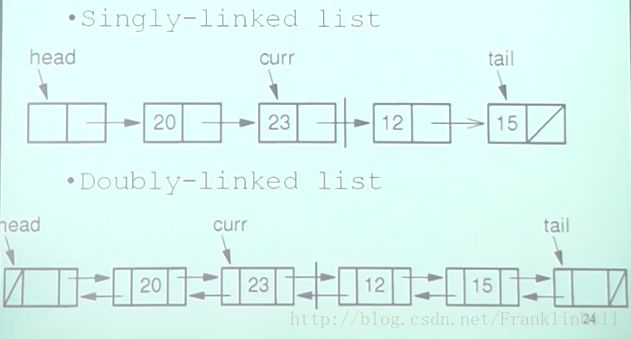
//singly-linked list node(单个的节点)
template <typename E> class Link{
public:
//两个数据域
E element;
Link *next;
//有元素值的
Link(const E& elemval, Link* nextval = NULL){
element = elemval;
next = nextval;
}
//无元素值的
Link(Link* nextval = NULL){
next = nextval;
}
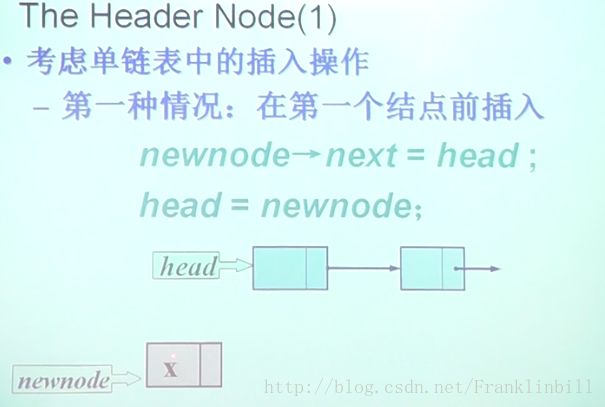
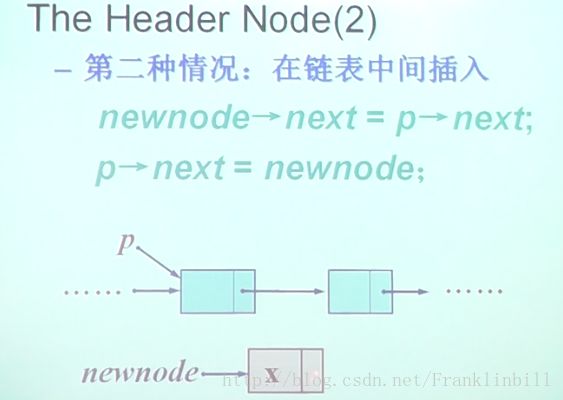
};汇总一下三种情况:
if(head == NULL || i == 0){
//插在表前
new node -> next = head;
if(head == NULL)
//原来为空表
head = newnode;
}else{
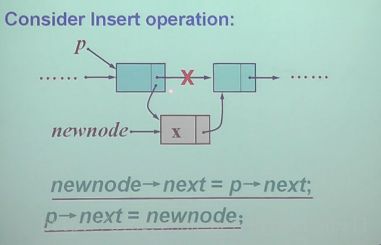
//插在表中还是末尾
new node ->next = p ->next;
if(p -> next == NULL)
tail = newnode;
p -> next = newnode;
}链表的删除操作:
//在链表中删除第i 个结点
if(i == 0){
//删除表中第0个结点
q = head; //q保存被删除结点地址
p = head = head ->next; //修改head
}else{
//删除表中或者表尾元素
q = p -> next;
p ->next = q -> next; // 重新链接
}
if(q == tail)
tail = p; //可能修改tail
delete q; //删除q注:带表头结点的单链表的作用:删除或者插入的时候代码量可以少很多
设置表头节点的目的是统一空表与非空白的操作,简化链表操作的实现。
list class
//Linked list implementation
template <typename E> class LList:
public List<E>{
private:
Link<E>* head;
Link<E>* tail;
Link<E>* curr;
int cnt;//元素个数
void init(){
curr = tail = head = new Link<E>;
cnt = 0;
}
}//删除所有节点(包括头结点)
void removeall(){
while(head != NULL){
curr = head;
head = head->next;
delete curr;
}
}
void moveToStart(){
curr = head;
}
void moveToEnd(){
curr = tail;
}
void next(){
if(curr != tail){
curr = curr->next;
}
}
int length() const{
return cnt;
}
//插入操作
template <typename E>
void LList<E>::insert(const E& it){
curr->next = new Link<E>(it, curr-> next);
if(tail == curr)
tail = curr->next;
cnt++;
}以上是个人对这一部分的一点小小的理解。如有问题欢迎指正,在此感谢您对我的支持。联系方式:[email protected]