【机器学习笔记36】蚁群算法-聚类分析
【参考资料】
【1】《模式识别与智能计算的MATLAB技术实现》
【2】《蚁群聚类算法综述》
1 算法概述
聚类数已知的算法流程
- 初始化蚁群参数,如蚂蚁数量、聚类数量等;每只蚂蚁对应一个解集:
| 样品号 | 1 | 2 | … | N |
|---|---|---|---|---|
| 蚂蚁 S i S_i Si | 类别1 | 类别2 | … | 类别1 |
上述表表示蚂蚁 S i S_i Si把N个样本分归属到分类中。
- 构建信息素矩阵
| 样本\类别 | 类别1 | 类别2 | 类别3 | 类别4 |
|---|---|---|---|---|
| 样本1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 样本2 | 0.1 | 0.1 | 0.1 | 0.1 |
| 样本3 | 0.1 | 0.1 | 0.1 | 0.1 |
| … | 0.1 | 0.1 | 0.1 | 0.1 |
| 样本N | 0.1 | 0.1 | 0.1 | 0.1 |
上述信息素 τ i j \tau_{ij} τij表示把第i个样本归类到第j个类别时的信息素
- 构建目标函数
假设: N个样品、M个模式分类 ∣ S j , j = 1 , 2 , . . . , M ∣ |S_j,j=1,2,..., M| ∣Sj,j=1,2,...,M∣,每个样品有n个特征。
目标: 将每个样品到聚类中心的距离和达到最小
m i n J ( w , c ) = ∑ j = 1 m ∑ i = 1 N ∑ p = 1 n w i j ∣ ∣ x i p − c j p ∣ ∣ 2 minJ(w, c)=\sum\limits_{j=1}^{m}\sum\limits_{i=1}^{N}\sum\limits_{p=1}^{n} w_{ij}||x_{ip} - c_{jp}||^2 minJ(w,c)=j=1∑mi=1∑Np=1∑nwij∣∣xip−cjp∣∣2
c j p = ∑ i = 1 N w i j x i p ∑ i = 1 N w i j c_{jp}=\dfrac{\sum\limits_{i=1}^{N}w_{ij}x_{ip}}{\sum\limits_{i=1}^{N}w_{ij}} cjp=i=1∑Nwiji=1∑Nwijxip
w i j = { 1 , N i ∈ S j 0 , N i ∉ S j w_{ij} = \begin{cases} 1, & N_i \in S_j \\ 0, & N_i \notin S_j \end{cases} wij={1,0,Ni∈SjNi∈/Sj样本属于该类则为1,否则为0
其中 x i p x_{ip} xip为第i个样本的p属性、 c j p c_{jp} cjp为第j个分类的p属性
- 更新蚁群
每一只蚂蚁在对自己解集中样本归属判断时采用两种策略(随机选择):
- 根据当前时刻信息素表,选择信息素高的;(直接基于既有知识)
- 按照当前信息素的概率,即信息素高的类别有更大的可能性被选择;(也是基于既有知识,但非直接,而是一定程度上的随机选择)
4.1 参考第一步每只蚂蚁所具备的解集;根据目标函数公式计算每只蚂蚁的目标值;
4.2 根据目标值将蚂蚁进行排序;
4.3 取最优的L只蚂蚁进行“局部搜索”,遍历这L只蚂蚁:
4.3.1 随机选择其中第i个样本,重新计算目标函数,确定一个新的分类;
4.3.2 当这只蚂蚁的若干个样本被重新分类后,再计算一次该蚂蚁的总目标函数,若解更优;则替换原解;
4.3.3 遍历L只蚂蚁后,前L只蚂蚁中具备最优解的作为当前全局最优解;
-
更新信息素表
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ s = 1 l Δ τ i j s \tau_{ij}(t+1)=(1-\rho)\tau_{ij}(t) + \sum\limits_{s=1}^{l}\Delta \tau_{ij}^s τij(t+1)=(1−ρ)τij(t)+s=1∑lΔτijs
其中若蚂蚁s中的样品i属于分类j,则 Δ τ i j s = Q J \Delta \tau_{ij}^s=\dfrac{Q}{J} Δτijs=JQ,否则为0。这里Q是一个超参数;J是蚂蚁s的目标函数值。 -
多次迭代后达到全局最优解
2 算法实现
实际在实现过程中感觉蚁群算法还是非常收到超参数影响。包括信息素的挥发参数,以及超参数Q等等,而且效果差距非常大。当前代码中的参数是一个具备比较好效果的设置。
# -*- coding: utf-8 -*-
import numpy as np
import sklearn.datasets as ds
import matplotlib.pyplot as plt
import random
import math
import operator
SAMPLE_NUM = 18 #样本数量
FEATURE_NUM = 2 #每个样本的特征数量
CLASS_NUM = 2 #分类数量
ANT_NUM = 200 #蚂蚁数量
"""
初始化测试样本,sample为样本,target_classify为目标分类结果用于对比算法效果
"""
sample, target_classify = ds.make_blobs(SAMPLE_NUM, n_features=FEATURE_NUM, centers=CLASS_NUM, random_state=3)
"""
信息素矩阵
"""
tao_array = [[random.random() for col in range(FEATURE_NUM)] for row in range(SAMPLE_NUM)]
"""
蚁群解集
"""
ant_array = [[0 for col in range(SAMPLE_NUM)] for row in range(ANT_NUM)]
t_ant_array = [[0 for col in range(SAMPLE_NUM)] for row in range(ANT_NUM)] #存储局部搜索时的临时解
"""
聚类中心点
"""
center_array = [[0 for col in range(FEATURE_NUM)] for row in range(CLASS_NUM)]
"""
当前轮次蚂蚁的目标函数值,前者是蚂蚁编号、后者是目标函数值
"""
ant_target = [(0, 0) for col in range(ANT_NUM)]
change_q = 0.3 #更新蚁群时的转换规则参数,表示何种比例直接根据信息素矩阵进行更新
L = 2 #局部搜索的蚂蚁数量
change_jp = 0.03 #局部搜索时该样本是否变动
change_rho = 0.02 #挥发参数
Q = 0.1 #信息素浓度参数
def _init_test_data():
"""
初始化蚁群解集,随机确认每只蚂蚁下每个样本的分类为1或者0
"""
for i in range(0, ANT_NUM):
for j in range(0, SAMPLE_NUM):
tmp = random.randint(0, FEATURE_NUM - 1)
ant_array[i][j] = tmp
"""
将前两个样本作为聚类中心点的初始值
"""
for i in range(0, CLASS_NUM):
center_array[i][0] = sample[random.randint(0, SAMPLE_NUM-1)][0]
center_array[i][1] = sample[random.randint(0, SAMPLE_NUM-1)][1]
def _get_best_class_by_tao_value(sampleid):
max_value = np.max(tao_array[sampleid])
for i in range(0, CLASS_NUM):
if max_value == tao_array[sampleid][i]:
return i
def random_pick(some_list, probabilities):
x = random.uniform(0,1)
cumulative_probability = 0.0
for item, item_probability in zip(some_list, probabilities):
cumulative_probability += item_probability
if x < cumulative_probability:break
return item
def _get_best_class_by_tao_probablity(sampleid):
tarray = np.array(tao_array[sampleid])
parray = tarray/np.sum(tarray)
return random_pick([0,1], parray)
def _update_ant():
"""
更新蚁群步骤
"""
#产生一个随机数矩阵
r = np.random.random((ANT_NUM, SAMPLE_NUM))
for i in range(0, ANT_NUM):
for j in range(0, SAMPLE_NUM):
if r[i][j] > change_q:
tmp_index = _get_best_class_by_tao_value(j)
#选择该样本中信息素最高的做为分类
ant_array[i][j] = tmp_index
else:
#计算概率值,根据概率的大小来确定一个选项
tmp_index = _get_best_class_by_tao_probablity(j)
ant_array[i][j] = tmp_index
#print(ant_array[i])
#1. 确定一个新的聚类中心
f_value_feature_0 = 0
f_value_feature_1 = 0
for i in range(0, CLASS_NUM):
f_num = 0
for j in range(0, ANT_NUM):
for k in range(0, SAMPLE_NUM):
if ant_array[j][k] == 0:
f_num += 1
f_value_feature_0 += sample[k][0] #特征1
else:
f_num += 1
f_value_feature_1 += sample[k][1] #特征2
if i == 0:
center_array[i][0] = f_value_feature_0/f_num
else:
center_array[i][1] = f_value_feature_1/f_num
#print(center_array[i], f_num)
def _judge_sample(sampleid):
"""
计算与当前聚类点的举例,判断该sample应所属的归类
"""
target_value_0 = 0
target_value_1 = 0
f1 = math.pow((sample[sampleid][0] - center_array[0][0]),2)
f2 = math.pow((sample[sampleid][1] - center_array[0][1]),2)
target_value_0 = math.sqrt(f1 + f2)
f1 = math.pow((sample[sampleid][0] - center_array[1][0]),2)
f2 = math.pow((sample[sampleid][1] - center_array[1][1]),2)
target_value_1 = math.sqrt(f1 + f2)
if target_value_0 > target_value_1:
return 1
else:
return 0
def _local_search():
"""
局部搜索逻辑
"""
#2. 根据新的聚类中心计算每个蚂蚁的目标函数
for i in range(0, ANT_NUM):
target_value = 0
for j in range(0, SAMPLE_NUM):
if ant_array[i][j] == 0:
#与分类0的聚类点计算距离
f1 = math.pow((sample[j][0] - center_array[0][0]),2)
f2 = math.pow((sample[j][1] - center_array[0][1]),2)
target_value += math.sqrt(f1 + f2)
else:
#与分类1的聚类点计算距离
f1 = math.pow((sample[j][0] - center_array[1][0]),2)
f2 = math.pow((sample[j][1] - center_array[1][1]),2)
target_value += math.sqrt(f1 + f2)
#保存蚂蚁i当前的目标函数
ant_target[i] = (i, target_value)
#3. 对全部蚂蚁的目标进行排序,选择最优的L只蚂蚁
ant_target.sort(key= operator.itemgetter(1)) #对ant进行排序
#4. 对这L只蚂蚁进行解的优化
for i in range(0, L):
ant_id = ant_target[i][0]
target_value = 0
for j in range(0, SAMPLE_NUM):
#对于该蚂蚁解集中的每一个样本
if random.random() < change_jp:
#将该样本调整到与当前某个聚类点最近的位置
t_ant_array[ant_id][j] = _judge_sample(j)
#判断是否保留这个临时解
for j in range(0, SAMPLE_NUM):
if t_ant_array[ant_id][j] == 0:
#与分类0的聚类点计算距离
f1 = math.pow((sample[j][0] - center_array[0][0]),2)
f2 = math.pow((sample[j][1] - center_array[0][1]),2)
target_value += math.sqrt(f1 + f2)
else:
#与分类1的聚类点计算距离
f1 = math.pow((sample[j][0] - center_array[1][0]),2)
f2 = math.pow((sample[j][1] - center_array[1][1]),2)
target_value += math.sqrt(f1 + f2)
if target_value < ant_target[i][1]:
#更新最优解
ant_array[ant_id] = t_ant_array[ant_id]
def _update_tau_array():
"""
更新信息素表
"""
for i in range(0, SAMPLE_NUM):
for j in range(0, CLASS_NUM):
tmp = tao_array[i][j] #当前的信息素
tmp = (1 - change_rho) * tmp #处理信息素挥发
J = 0
#处理信息素浓度增加
for k in range(0, ANT_NUM):
if ant_array[k][i] == j:
f1 = math.pow((sample[i][0] - center_array[j][0]),2)
f2 = math.pow((sample[i][1] - center_array[j][1]),2)
J += math.sqrt(f1 + f2)
if J != 0:
tmp += Q/J
#print(tmp, Q/J)
tao_array[i][j] = tmp
#print(np.var(tao_array))
"""
说明:
简单蚁群算法解决聚类问题,参考笔记《蚁群算法-聚类算法》
作者:fredric
日期:2018-12-21
"""
if __name__ == "__main__":
_init_test_data();
for i in range(0, 100):
print("iterate No. {} target {}".format(i, ant_target[0][1]))
_update_ant()
_local_search()
_update_tau_array()
#画出分类
pre = ant_array[ant_target[0][0]]
plt.figure(figsize=(5, 6), facecolor='w')
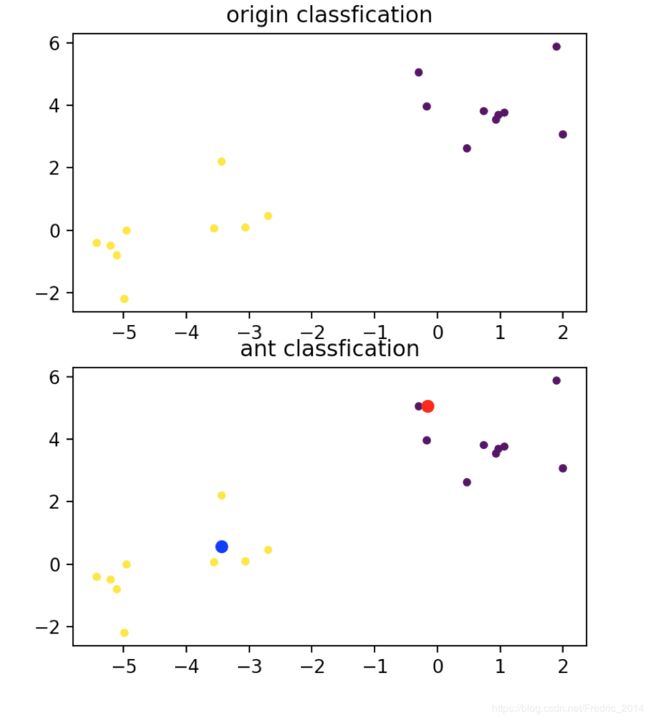
plt.subplot(211)
plt.title('origin classfication')
plt.scatter(sample[:, 0], sample[:, 1], c=target_classify, s=20, edgecolors='none')
plt.subplot(212)
plt.title('ant classfication')
plt.scatter(sample[:, 0], sample[:, 1], c=pre, s=20, edgecolors='none')
plt.plot(center_array[0][0], center_array[0][1],'ro')
plt.plot(center_array[1][0], center_array[1][1],'bo')
plt.show()