LCATarjan离线算法

怎么说离线算法呢，我觉得就是说你把想要询问的东西提前存起来了，这样在遍历然后顺便建树的过程中就可以随时回答这个问题，然后再进行相应的更新…

http://www.cnblogs.com/JVxie/p/4854719.html
☝这个博主写得很不错，我就是这么看懂的。

#include
using namespace std;
#include
#include
#include
vector<int>node[40010];//存相邻的点
vector<int>value[40010];//存相邻的边权
vector<int>query[40010];//存与i点相关的询问
vector<int>num[40010];//存第几次询问
int vis[40010];
int f[40010];
int dis[40010];//dis数组用来存每个点到根节点的距离，dis【i】表示i到根节点的距离
int pr[210];//存答案

int find(int x)
{
    while (f[x] != x)
        x = f[x];
    return x;
}

void join(int x, int y)
{
    int fx = find(x);
    int fy = find(y);
    if (f[fx] != fy)
        f[fx] = fy;
}

void TarjanLCA(int root, int weight)
{
    f[root] = root;
    vis[root] = 1;
    dis[root] = weight;
    for (int i = 0; i < node[root].size(); i++)
    {
        int nextnode = node[root][i];
        int nextw = value[root][i];
        if (!vis[nextnode])
        {
            TarjanLCA(nextnode, weight + nextw);
            join(nextnode, root);
        }
    }
    for (int i = 0; i < query[root].size(); i++)
    {
        int neednode = query[root][i];
        if (vis[neednode])
            pr[num[root][i]] = dis[root] + dis[neednode] - 2 * dis[find(neednode)];
    }
}

void init(int n)
{
    memset(vis, 0, sizeof(vis));
    memset(dis, 0, sizeof(dis));
    memset(pr, 0, sizeof(pr));
    for (int i = 1; i <= n; i++)
    {
        node[i].clear();
        query[i].clear();
        num[i].clear();
        value[i].clear();
    }
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n, m;
        cin >> n >> m;
        init(n);
        for (int i = 0; i < n - 1; i++)
        {
            int u, v, w;
            cin >> u >> v >> w;
            node[u].push_back(v);
            node[v].push_back(u);
            value[u].push_back(w);
            value[v].push_back(w);
        }
        for (int i = 0; i < m; i++)
        {
            int u, v;
            cin >> u >> v;
            query[u].push_back(v);//存下询问的两个点
            query[v].push_back(u);
            num[u].push_back(i);//存这是第几次询问了
            num[v].push_back(i);
        }
        TarjanLCA(1, 0);
        for (int i = 0; i < m; i++)
            cout << pr[i]<return 0;
}

☝贴一份模板，带权值的，当然我觉得LCA核心还是找最近公共祖先，权值是一个相当于副产品。

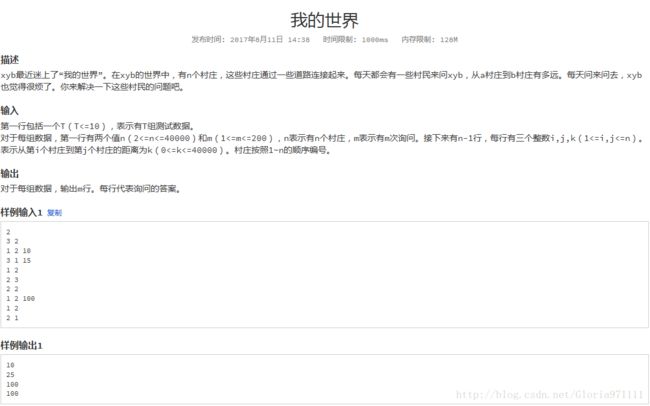
这是题目http://101.200.220.237/contest/50/problem/294/

下面我自己模拟一下一个LCA的询问，time to 胡言乱语。

假设我们有一组数据 9个节点 8条边 联通情况如下：1–2，1–3，2–4，2–5，3–6，5–7，5–8，7–9
设我们要查找最近公共祖先的点为：9–8，4–6，7–5，5–3

下面我们开始跑程序。
输入结束后，1的子节点有2,3；2的子节点1,4,5；3的子节点有1,6；4的子节点有2；5的子节点有2，7,8；6的子节点有3；7的子节点有5,9；8的子节点有5；9的子节点有7；

询问的过程是8，9有关，4,6有关，7,5有关，5,3有关；

开始建树，这里的边权都是0，先不管，从1开始，Tarjan（1,0）。f【1】=1,1标记访问过，dis【1】=0；发现1有2个儿子，遍历，先是2，发现2没有被访问过，然后进入Tarjan（2,0），f【2】=2,2标记访问过，dis【2】=0；发现2有三个儿子，遍历，先是1，结果1被访问过，然后是4，发现4没有被访问过，进入Tarjan（4,0），f【4】=4,4标记被访问过，然后发现4有一个儿子2已经被访问过了，所以4寻找儿子的过程已经结束，进入询问，问6，结果6没有被访问过，所以结束询问，返回到Tarjan（4,0）执行完的地方，然后join（4,2），所以此时f【4】=2，继续走，进入2的第二个儿子5，发现没有被标记，进入Tarjan（5,0），f【5】=5,5被标记访问过，5有两个儿子，进入Tarjan（8,0），结束儿子访问，进入询问，与8有关的9还没有被标记，所以结束，join（8,5），所以f【8】=5，然后继续访问5的儿子7，进入Tarjan（7,0），f【7】=7,7标记被访问，发现7有一个未被标记的儿子9，然后进入Tarjan（9,0），f【9】=9,9标记为被访问，然后9没有有效儿子，进入询问，9和8有关系，发现8被标记过，那么8和9的最近公共祖先就是find（8）=5，因为这此时还是在这棵子树中，让我们继续走看看，然后结束询问join（9,7），此时f【9】=7，然后7的儿子都遍历结束，进入询问，7和5有关系，发现5已经被标记过了，所以7和5的最近公共祖先就是find（5）=5,询问结束，然后返回到join（7,5），此时f【7】=5，5的儿子遍历结束，然后就是询问，询问发现5和3有关系但是3还未被标记，所以继续向前走，join（5,2），此时f【5】=2，然后发现2的儿子访问结束，进入询问，发现没有询问，join（2,1），此时f【2】=1，此时继续访问1的另一个儿子3，f【3】=3，3标记为访问过，3有一个儿子6，进入Tarjan（6,0），f【6】=6,6标记为访问过，然后继续走发现6没有有效儿子，然后进入询问，询问发现4，然后4被标记，那么6和4的最近公共祖先就是find（4）=1，然后继续走join（6,3），此时f【6】=3，然后3对儿子的访问结束，进入询问，发现5被访问过，所以5和3的最近公共祖先就是find（5）=1，然后回到join（3,1），此时f【3】=1，然后发现对1的儿子的遍历结束，进入询问，发现没有询问，over！
所以我们的这些访问出结果的顺序是9-8,7-5,4-6,5-3，这其实就是利用的还是建树的过程，在逐步建树的过程中完成这些询问，非常机智！
边权的问题就是开一个dis数组，存每一个点到根节点的距离，然后最后减去两倍的dis【最近公共祖先】，dis数组的取值是一个不断累加的过程。

自己跑一遍程序就会好很多，而且我发现跑这种程序需要找一个合适大小的树，太大比较复杂，太小也不好，看着简单，但是体会不到算法的过程和巧妙之处！