中文相似度匹配算法

经典算法1---相似度--模糊查询，查抄袭，语言识别

1.百度百科介绍：

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。

许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

编辑距离的算法是首先由俄国科学家Levenshtein提出的，故又叫Levenshtein Distance。

2.用途

模糊查询

3.实现过程

a.首先是有两个字符串,这里写一个简单的 abc和abe

b.将字符串想象成下面的结构。

A处 是一个标记，为了方便讲解，不是这个表的内容。

 

	abc	a	b	c
abe	0	1	2	3
a	1	A处
b	2
e	3

c.来计算A处 出得值

它的值取决于：左边的1、上边的1、左上角的0.

按照Levenshtein distance的意思：

上面的值和左面的值都要求加1，这样得到1+1=2。

A处 由于是两个a相同，左上角的值加0.这样得到0+0=0。

这是后有三个值，左边的计算后为2，上边的计算后为2，左上角的计算为0，所以A处 取他们里面最小的0.

d.于是表成为下面的样子

	abc	a	b	c
abe	0	1	2	3
a	1	0
b	2	B处
e	3

在B处 会同样得到三个值，左边计算后为3，上边计算后为1，在B处 由于对应的字符为a、b，不相等，所以左上角应该在当前值的基础上加1，这样得到1+1=2，在（3,1,2）中选出最小的为B处的值。

e.于是表就更新了

 

	abc	a	b	c
abe	0	1	2	3
a	1	0
b	2	1
e	3	C处

C处 计算后：上面的值为2，左边的值为4，左上角的：a和e不相同，所以加1，即2+1，左上角的为3。

在（2,4,3）中取最小的为C处 的值。

f.于是依次推得到

		a	b	c
	0	1	2	3
a	1	A处 0	D处 1	G处 2
b	2	B处 1	E处 0	H处 1
e	3	C处 2	F处 1	I处 1

 

I处: 表示abc 和abe 有1个需要编辑的操作。这个是需要计算出来的。

同时，也获得一些额外的信息。

A处: 表示a      和a      需要有0个操作。字符串一样

B处: 表示ab    和a      需要有1个操作。

C处: 表示abe  和a      需要有2个操作。

D处: 表示a      和ab    需要有1个操作。

E处: 表示ab    和ab    需要有0个操作。字符串一样

F处: 表示abe  和ab    需要有1个操作。

G处: 表示a      和abc   需要有2个操作。

H处: 表示ab    和abc    需要有1个操作。

I处: 表示abe   和abc    需要有1个操作。

g.计算相似度

先取两个字符串长度的最大值maxLen，用1-（需要操作数除maxLen），得到相似度。

例如abc 和abe 一个操作，长度为3，所以相似度为1-1/3=0.666。

4.代码实现

直接能运行， 复制过去就行。

package code;

/**
 * @className:MyLevenshtein.java
 * @classDescription:Levenshtein Distance 算法实现
 * 可以使用的地方：DNA分析 　　拼字检查 　　语音辨识 　　抄袭侦测
 * @author:donghai.wan
 * @createTime:2012-1-12
 */
public class MyLevenshtein {

    public static void main(String[] args) {
        //要比较的两个字符串
        String str1 = "今天星期四";
        String str2 = "今天是星期五";
        levenshtein(str1,str2);
    }

    /**
     * 　　DNA分析 　　拼字检查 　　语音辨识 　　抄袭侦测
     *
     * @createTime 2012-1-12
     */
    public static void levenshtein(String str1,String str2) {
        //计算两个字符串的长度。
        int len1 = str1.length();
        int len2 = str2.length();
        //建立上面说的数组，比字符长度大一个空间
        int[][] dif = new int[len1 + 1][len2 + 1];
        //赋初值，步骤B。
        for (int a = 0; a <= len1; a++) {
            dif[a][0] = a;
        }
        for (int a = 0; a <= len2; a++) {
            dif[0][a] = a;
        }
        //计算两个字符是否一样，计算左上的值
        int temp;
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                    temp = 0;
                } else {
                    temp = 1;
                }
                //取三个值中最小的
                dif[i][j] = min(dif[i - 1][j - 1] + temp, dif[i][j - 1] + 1,
                        dif[i - 1][j] + 1);
            }
        }
        System.out.println("字符串\""+str1+"\"与\""+str2+"\"的比较");
        //取数组右下角的值，同样不同位置代表不同字符串的比较
        System.out.println("差异步骤："+dif[len1][len2]);
        //计算相似度
        float similarity =1 - (float) dif[len1][len2] / Math.max(str1.length(), str2.length());
        System.out.println("相似度："+similarity);
    }

    //得到最小值
    private static int min(int... is) {
        int min = Integer.MAX_VALUE;
        for (int i : is) {
            if (min > i) {
                min = i;
            }
        }
        return min;
    }

}

package code;  
  
/** 
 * @className:MyLevenshtein.java 
 * @classDescription:Levenshtein Distance 算法实现 
 * 可以使用的地方：DNA分析 　　拼字检查 　　语音辨识 　　抄袭侦测 
 * @author:donghai.wan 
 * @createTime:2012-1-12 
 */  
public class MyLevenshtein {  
  
    public static void main(String[] args) {  
        //要比较的两个字符串  
        String str1 = "今天星期四";  
        String str2 = "今天是星期五";  
        levenshtein(str1,str2);  
    }  
  
    /** 
     * 　　DNA分析 　　拼字检查 　　语音辨识 　　抄袭侦测 
     *  
     * @createTime 2012-1-12 
     */  
    public static void levenshtein(String str1,String str2) {  
        //计算两个字符串的长度。  
        int len1 = str1.length();  
        int len2 = str2.length();  
        //建立上面说的数组，比字符长度大一个空间  
        int[][] dif = new int[len1 + 1][len2 + 1];  
        //赋初值，步骤B。  
        for (int a = 0; a <= len1; a++) {  
            dif[a][0] = a;  
        }  
        for (int a = 0; a <= len2; a++) {  
            dif[0][a] = a;  
        }  
        //计算两个字符是否一样，计算左上的值  
        int temp;  
        for (int i = 1; i <= len1; i++) {  
            for (int j = 1; j <= len2; j++) {  
                if (str1.charAt(i - 1) == str2.charAt(j - 1)) {  
                    temp = 0;  
                } else {  
                    temp = 1;  
                }  
                //取三个值中最小的  
                dif[i][j] = min(dif[i - 1][j - 1] + temp, dif[i][j - 1] + 1,  
                        dif[i - 1][j] + 1);  
            }  
        }  
        System.out.println("字符串\""+str1+"\"与\""+str2+"\"的比较");  
        //取数组右下角的值，同样不同位置代表不同字符串的比较  
        System.out.println("差异步骤："+dif[len1][len2]);  
        //计算相似度  
        float similarity =1 - (float) dif[len1][len2] / Math.max(str1.length(), str2.length());  
        System.out.println("相似度："+similarity);  
    }  
  
    //得到最小值  
    private static int min(int... is) {  
        int min = Integer.MAX_VALUE;  
        for (int i : is) {  
            if (min > i) {  
                min = i;  
            }  
        }  
        return min;  
    }  
  
}  

5.猜测原理

from   http://www.lanceyan.com/tech/arch/simhash_hamming_distance_similarity.html

通过 采集系统 我们采集了大量文本数据，但是文本中有很多重复数据影响我们对于结果的分析。分析前我们需要对这些数据去除重复，如何选择和设计文本的去重算法？常见的有余弦夹角算法、欧式距离、Jaccard相似度、最长公共子串、编辑距离等。这些算法对于待比较的文本数据不多时还比较好用，如果我们的爬虫每天采集的数据以千万计算，我们如何对于这些海量千万级的数据进行高效的合并去重。最简单的做法是拿着待比较的文本和数据库中所有的文本比较一遍如果是重复的数据就标示为重复。看起来很简单，我们来做个测试，就拿最简单的两个数据使用Apache提供的 Levenshtein for 循环100w次计算这两个数据的相似度。代码结果如下：

             String s1  =  "你妈妈喊你回家吃饭哦，回家罗回家罗"  ;
             String s2  =  "你妈妈叫你回家吃饭啦，回家罗回家罗"  ;

             long t1  =  System. currentTimeMillis ( ) ;

             for  ( int i  =  0 ; i  <  1000000 ; i ++ )  {
                    int dis  = StringUtils . getLevenshteinDistance (s1, s2 ) ;
             }

             long t2  =  System. currentTimeMillis ( ) ;

             System.  out . println ( " 耗费时间： "  +  (t2  - t1 )  +  "  ms " ) ;

耗费时间： 4266 ms

大跌眼镜，居然计算耗费4秒。假设我们一天需要比较100w次，光是比较100w次的数据是否重复就需要4s，就算4s一个文档，单线程一分钟才处理15个文档，一个小时才900个，一天也才21600个文档，这个数字和一天100w相差甚远，需要多少机器和资源才能解决。

为此我们需要一种应对于海量数据场景的去重方案，经过研究发现有种叫 local sensitive hash 局部敏感哈希 的东西，据说这玩意可以把文档降维到hash数字，数字两两计算运算量要小很多。查找很多文档后看到google对于网页去重使用的是simhash，他们每天需要处理的文档在亿级别，大大超过了我们现在文档的水平。既然老大哥也有类似的应用，我们也赶紧尝试下。simhash是由 Charikar 在2002年提出来的，参考 《Similarity estimation techniques from rounding algorithms》 。 介绍下这个算法主要原理，为了便于理解尽量不使用数学公式，分为这几步：

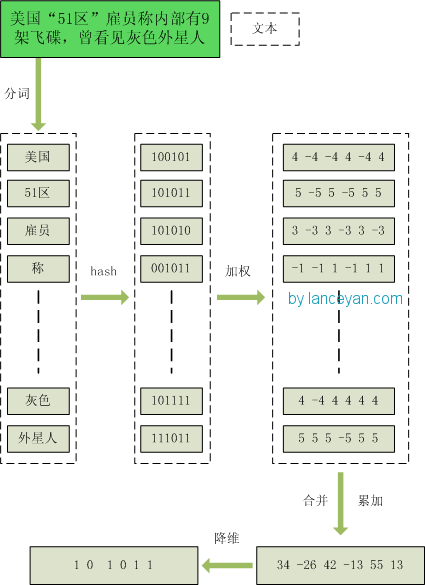
• 1、分词，把需要判断文本分词形成这个文章的特征单词。最后形成去掉噪音词的单词序列并为每个词加上权重，我们假设权重分为5个级别（1~5）。比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要。

• 2、hash，通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。这样我们的字符串就变成了一串串数字，还记得文章开头说过的吗，要把文章变为数字计算才能提高相似度计算性能，现在是降维过程进行时。

• 3、加权，通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。

• 4、合并，把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。

• 5、降维，把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的simhash签名。 如果每一位大于0 记为 1，小于0 记为 0。最后算出结果为：“1 0 1 0 1 1”。

整个过程图为：

大家可能会有疑问，经过这么多步骤搞这么麻烦，不就是为了得到个 0 1 字符串吗？我直接把这个文本作为字符串输入，用hash函数生成 0 1 值更简单。其实不是这样的，传统hash函数解决的是生成唯一值，比如 md5、hashmap等。md5是用于生成唯一签名串，只要稍微多加一个字符md5的两个数字看起来相差甚远；hashmap也是用于键值对查找，便于快速插入和查找的数据结构。不过我们主要解决的是文本相似度计算，要比较的是两个文章是否相识，当然我们降维生成了hashcode也是用于这个目的。看到这里估计大家就明白了，我们使用的simhash就算把文章中的字符串变成 01 串也还是可以用于计算相似度的，而传统的hashcode却不行。我们可以来做个测试，两个相差只有一个字符的文本串，“你妈妈喊你回家吃饭哦，回家罗回家罗” 和 “你妈妈叫你回家吃饭啦，回家罗回家罗”。

通过simhash计算结果为：

1000010010101101111111100000101011010001001111100001001011001011

1000010010101101011111100000101011010001001111100001101010001011

通过 hashcode计算为：

1111111111111111111111111111111110001000001100110100111011011110

1010010001111111110010110011101

大家可以看得出来，相似的文本只有部分 01 串变化了，而普通的hashcode却不能做到，这个就是局部敏感哈希的魅力。目前Broder提出的shingling算法和Charikar的simhash算法应该算是业界公认比较好的算法。在simhash的发明人Charikar的论文中并没有给出具体的simhash算法和证明，“量子图灵”得出的证明simhash是由随机超平面hash算法演变而来的。

现在通过这样的转换，我们把库里的文本都转换为simhash 代码，并转换为long类型存储，空间大大减少。现在我们虽然解决了空间，但是如何计算两个simhash的相似度呢？难道是比较两个simhash的01有多少个不同吗？对的，其实也就是这样，我们通过海明距离（Hamming distance）就可以计算出两个simhash到底相似不相似。两个simhash对应二进制（01串）取值不同的数量称为这两个simhash的海明距离。举例如下： 10101 和 00110 从第一位开始依次有第一位、第四、第五位不同，则海明距离为3。对于二进制字符串的a和b，海明距离为等于在a XOR b运算结果中1的个数（普遍算法）。

为了高效比较，我们预先加载了库里存在文本并转换为simhash code 存储在内存空间。来一条文本先转换为 simhash code，然后和内存里的simhash code 进行比较，测试100w次计算在100ms。速度大大提升。

未完待续：

1、目前速度提升了但是数据是不断增量的，如果未来数据发展到一个小时100w，按现在一次100ms，一个线程处理一秒钟 10次，一分钟 60 * 10 次，一个小时 60*10 *60 次 = 36000次，一天 60*10*60*24 = 864000次。 我们目标是一天100w次，通过增加两个线程就可以完成。但是如果要一个小时100w次呢？则需要增加30个线程和相应的硬件资源保证速度能够达到，这样成本也上去了。能否有更好的办法，提高我们比较的效率？

2、通过大量测试，simhash用于比较大文本，比如500字以上效果都还蛮好，距离小于3的基本都是相似，误判率也比较低。但是如果我们处理的是微博信息，最多也就140个字，使用simhash的效果并不那么理想。看如下图，在距离为3时是一个比较折中的点，在距离为10时效果已经很差了，不过我们测试短文本很多看起来相似的距离确实为10。如果使用距离为3，短文本大量重复信息不会被过滤，如果使用距离为10，长文本的错误率也非常高，如何解决？

另：相似度方法综述！！！

from http://blog.csdn.net/wangzhiqing3/article/details/8293286