机器人学统计建模中的高斯分布（Gaussian distribution in robotics statistic model）

1.为什么是高斯分布？是什么让高斯分布变得有用而且重要呢？

a.描述高斯分布只需要俩个参数，它们是均值和方差，它们就是该分布的本质信息。（Only two parameters）
b.高斯分布具有一些很好的数学性质，例如：多个高斯分布的乘积可以形成另一个高斯分布。（Good mathematical properties）
c.中心极限定理告诉我们任何随机变量的样本均值的期望都收敛于高斯分布。（Central limit theorem）
以上说明高斯分布是一个为噪声和不确定性建模的合适选择。

2.最大似然估计（MLE）

似然（Likelihood）的定义：似然是当给定模型参数时，随机变量取到观测值的概率，下标 $i$ 表示一次特定的观察，在$x$的多个测量值中，这次观察结果被记为$x_i$。

$Likelihood：p(\left\{\begin{array}{c}{x}_i\end{array}\right\}|\mu ,\sigma )$，其中 $\left\{\begin{array}{c}{x}_i\end{array}\right\}$为观测数据（observed data），$\mu ,\sigma$为未知参数（unknown parameters） （代表着给定参数，观测到所有数据可能性，所以越大越好）

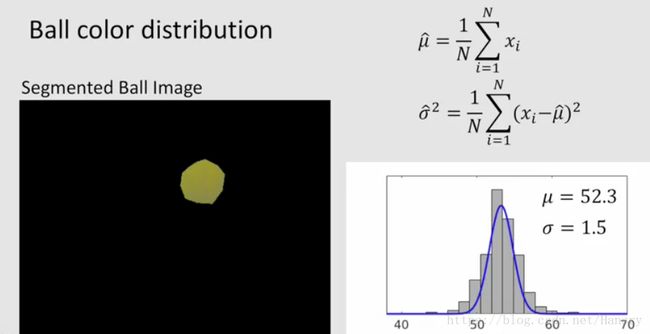
假如我们有一个小球，如下面图片所示，那我们怎么来用高斯模型（要求确定$\mu ,\sigma$）来描述其像素值的分布，可以用极大似然法的方法来估计。

怎么通过观察到的数据来估计高斯模型的均值和方差？

(1) 这里需要强调的是，我们拥有数据，而我们需要去估计的是模型的参数。我们对于给定观测数据时，能将似然函数最大化的参数很感兴趣。

如果用数学的方式来表达刚才讲的，我们可以这么写：
$\hat{\mu },\hat{\sigma }=arg\underset{\mu ,\sigma }{\max }(\left\{\begin{array}{c}{x}_i\end{array}\right\}|\mu ,\sigma )$
其中 $\hat{\mu },\hat{\sigma }$ 表示对 $\mu ,\sigma$的估计 。

我们需要最大化的似然函数是所有样本数据的联合概率，如果每个观测不是独立的，问题将很棘手。如果我们假设每一个观测之间都是相互独立的，联合似然概率就可以表达为关于每个样本的似然函数的乘积，公式如下所示：
$p(\left\{\begin{array}{c}{x}_i\end{array}\right\}|\mu ,\sigma )={\prod }_{i=1}^{N}p(x_i|\mu ,\sigma )$

在这种情况下，我们试着计算$\mu$和$\sigma$的极大似然估计。

由于对数具有单调递增的性质，所以我们最大化似然函数的时候，可以利用对数函数的性质，通过最大化对数似然函数就能找到参数值的极大似然估计，虽然函数值是不同的，但是使目标函数达到最大值的参数值却是一样的。

$$\begin{gathered} arg\underset{\mu ,\sigma }{\max }{\prod }_{i=1}^{N}p(x_i|\mu ,\sigma ) \\ =arg\underset{\mu ,\sigma }{\max }ln\left\{\begin{array}{c}{\prod }_{i=1}^{N}p(x_i|\mu ,\sigma )\end{array}\right\} \\ =arg\underset{\mu ,\sigma }{\max }{\sum }_{i=1}^{N}lnp(x_i|\mu ,\sigma ) \end{gathered}$$

从上面公式中，利用对数函数的性质，我们将最大化似然函数转化为每个测量量的似然取对数后的和。

因此，问题就转换为找到$\mu ,\sigma$,使得每个测量量的似然的对数和最大。

(2) 这里值得注意的是，我们的所用的似然函数为高斯模型：
$p(x_i|\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }exp\left\{\begin{array}{c}-\frac{(x_i-\mu )}{2{\sigma }^2}\end{array}\right\}$

利用对数的形式，我们可以转换为：
$ln \ p(x_{i}|\mu, \sigma) \=ln \frac{1}{\sqrt{2\pi}\ \sigma}exp \begin{Bmatrix}{- \frac{(x_{i}-\mu)}{2 \sigma^{2}}}\end{Bmatrix} \= \begin{Bmatrix}{- \frac{(x_{i}-\mu)}{2 \sigma^{2}}-ln \sigma - ln \sqrt{2 \pi}}\end{Bmatrix} $

因此，
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
$$\begin{gathered} \hat{\mu },\hat{\sigma } \\ =arg\underset{\mu ,\sigma }{\max }{\sum }_{i=1}^N\left\{\begin{array}{c}-\frac{(x_i-\mu )}{2{\sigma }^2}-ln\sigma -ln\sqrt{2\pi }\end{array}\right\} \\ =arg\underset{\mu ,\sigma }{\max }{\sum }_{i=1}^N\left\{\begin{array}{c}-\frac{(x_i-\mu )}{2{\sigma }^2}-ln\sigma \end{array}\right\}(其中-ln\sqrt{2\pi }不影响结果，所以将其去掉) \\ =arg\underset{\mu ,\sigma }{\min }{\sum }_{i=1}^N\left\{\begin{array}{c}\frac{(x_i-\mu )}{2{\sigma }^2}+ln\sigma \end{array}\right\}(将其转化为最小化问题，尽管这俩个问题是等价的，但是最小化是优化问题的标准形式) \end{gathered}$$
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
我们令 $J(\mu ,\sigma )={\sum }_{i=1}^N\left\{\begin{array}{c}\frac{(x_i-\mu )}{2{\sigma }^2}+ln\sigma \end{array}\right\}$，故优化问题变为$\hat{\mu},\hat{\sigma} =arg \ \underset{\mu,\sigma}{min}J(\mu,\sigma) $

在优化过程中，
1.我们先对$\mu$求偏导，并令其等于0，得到$\hat{\mu }$： $\frac{\partial J}{\partial \mu }=0\to \hat{u}$
2. 用$\hat{\mu }$代替$\mu$再对$\sigma$求偏导，令其等于0，得到$\hat{\sigma }$： $\frac{\partial J（\hat{u},\sigma ）}{\partial \sigma }=0\to \hat{\sigma }$

最后得到一个很简单的结果（具体详细推导这里省略）：
$\hat{\mu }=\frac{1}{N}{\sum }_{i=1}^N{x}_i$, 样本的均值
${\hat{\sigma }}^2=\frac{1}{N}{\sum }_{i=1}^N(x_i-\hat{\mu }{)}^2$， 样本的方差

通过以上推导，我们就可以确定小球像素的分布了。

3.多变量高斯分布（Multivariate Guassian）

多变量高斯分布使用了多个变量，因此它能够使用更丰富的特征对目标建模，让我们重新思考之前的小球颜色的例子，在那个例子中，我们使用单变量$\mu$,然而颜色本身可以从多个维度来描述，例如，彩色照片经常通过三个颜色通道定义红、绿、蓝。

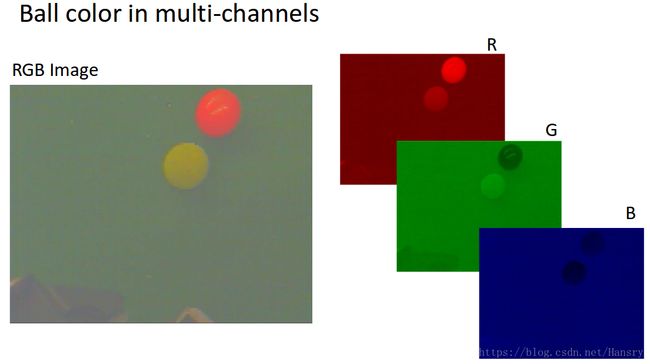
如果我们在3D图中画出所有像素的RGB值，就能得到如下的色彩分布：

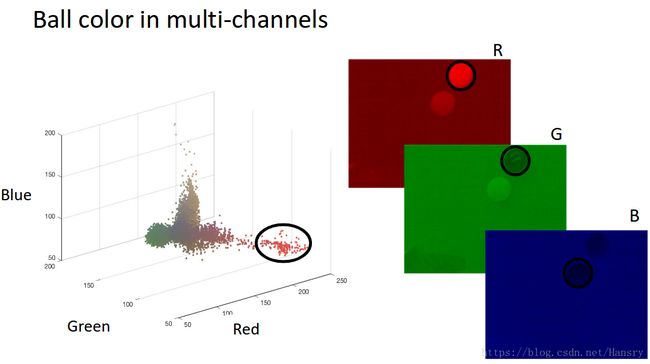
现在考虑使用RGB三通道模型来对红球色彩进行建模。让我们来讨论下在这个例子中高斯分布是怎么工作的。

数学上，多变量高斯分布表示为指数形式（exponential）和比例因子相乘的形式，

$p(x)=\frac{1}{(2\pi {)}^{D/2}|\sum {|}^{1/2}}exp\left\{\begin{array}{c}-\frac{1}{2}(x-\mu {)}^T{\sum }^{-1}\ast (x-\mu )\end{array}\right\}$

其中：
D表示维度的数量，如果为RGB，那么D=3。
$\mathbf{x}$ 表示样本变量，同时也是一个向量（元素代表各个维度样本的值），我希望获得它们的概率模型。
我们希望得到在高斯分布(Gaussian distribution) $\mathbf{x}$ 的概率。
$\mu$ 表示均值，同时也是向量。
$\sum$ 表示协方差矩阵(covariance matrix)，是一个方阵(square matrix)。对于协方差矩阵，由俩个部分组成：对角的项(Diagonal terms)和非对角的项(off-diagonal terms)。对于RGB三个通道的图片，其协方差矩阵是3x3的一个矩阵，如下所示：
$\sum =\left[\begin{array}{ccc}{\sigma }_{x_1}^2& {\sigma }_{x_1}{\sigma }_{x_2}& {\sigma }_{x_1}{\sigma }_{x_3}\\ {\sigma }_{x_2}{\sigma }_{x_1}& {\sigma }_{x_2}^2& {\sigma }_{x_2}{\sigma }_{x_3}\\ {\sigma }_{x_3}{\sigma }_{x_1}& {\sigma }_{x_3}{\sigma }_{x_2}& {\sigma }_{x_3}^2\end{array}\right]$

对角线代表变量 $x_1、x_2、x_3$各自的独立方差，非对角项${\sigma }_{x1}{\sigma }_{x2}$、${\sigma }_{x2}{\sigma }_{x3}$ 等代表了俩个变量的相关性。相关性部分代表了一个变量相对于另一个变量的相关程度。
$|\sum |$ 代表协方差矩阵的行列式。

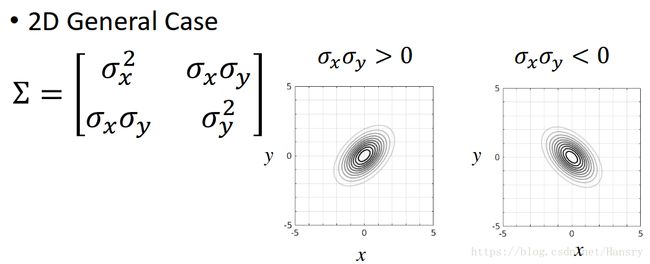
让我们来用蓝色的球举一个例子，我们现在正在处理3维变量RGB，变量的向量包含了我们在红色、绿色、蓝色通道的样本像素值。因此，其均值将是3x1的向量，协方差矩阵将会是3x3的矩阵。

$p(\mathbf{x})$是指某个样本像素（向量，为$\mathbf{x}$）在假设我们知道了小球RGB模型的均值和方差的条件下从小球RGB模型（三维高斯模型）抽出的概率。

对于2D的情况，我们令$\mathbf{x}=[xy{]}^T$、$\mu =[00{]}^T$、KaTeX parse error: Expected & or \\ or \cr or \end at position 32: …atrix} 1 & 0 \\\̲ ̲0 & 1 \\ \end{…, 则如下所示，其中，当从上面往下看的时候，我们会发现其等高线上的概率是一样的。由于协方差是个对角矩阵且对角线上的值是一样的，所以等高线是一个圆。

最里面的圆代表着概率的峰值，外面的圆代表这概率较小的区域

以下列举几种当参数变化时高斯分布的变化情况：

1. 均值发生变化：x维度均值变大，y维度均值变小
   
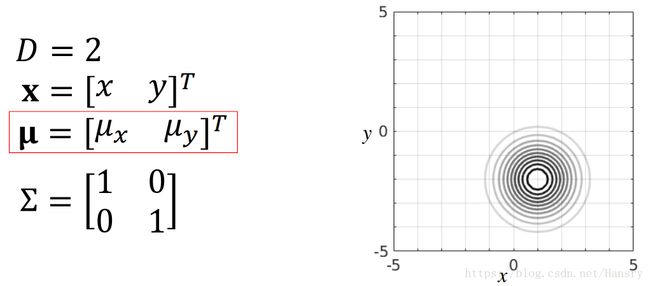
2. 协方差矩阵中随机变量的独立方差的值发生变化：${\sigma }^2$变大
   
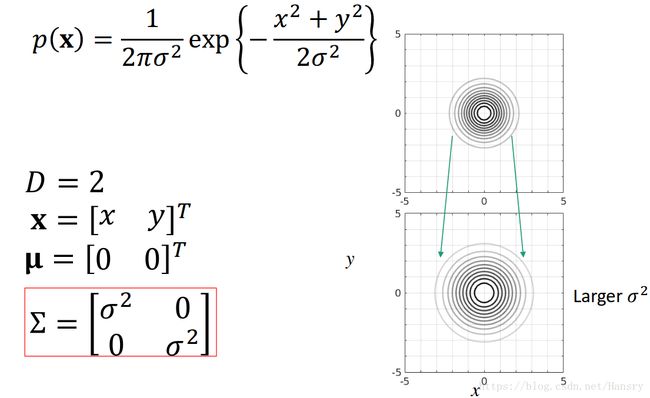
3. 当协方差矩阵中非对角线上的值不同时，即俩个随机变量具有相关性（这时侯模型的有些性质在2D投影其实是看不到的）。其中分为${\sigma }_x{\sigma }_y>0$ 和 ${\sigma }_x{\sigma }_y<0$。
   

其中$\sum$有俩个特殊的性质：
1.协方差矩阵必须是特殊的正定对称矩阵，这意味着协方差矩阵的元素是关于对角线对称的，因此，$\sum$的特征值（eigen value）必须为正的。
2.即使$\sum$矩阵有非0的相关项，我们总可以找到一种坐标变换让分布的形状变成对称的。我们可以使用特征值分解算法，来将协方差进行矩阵分解进而得到这些变换。$\sum$可以被分解成$UD{U}^T$的形式，其中$D$是对角矩阵。

4.多变量高斯分布下的最大似然估计（MLE of Multivariate Gausssian）

如何从观测数据计算和估计多维高斯模型的参数。

多维高斯模型拥有俩个参数：$\mu$ 和$\sum$

Likelihood（似然）: 是一个给定的参数未知的模型产生这个观测数据{$x_i$}(请注意这里是$x_i$的集合)的概率。

根据上面一维高斯函数的推导，同样的，我们可以利用其思想，最后得到 (详细推导)：

$\hat{\mu }=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{x}}_{\mathbf{i}}$

$\hat{\sum }=\frac{1}{N}{\sum }_{i=1}^N({\mathbf{x}}_{\mathbf{i}}-\hat{\mu })({\mathbf{x}}_{\mathbf{i}}-\hat{\mu }{)}^T$

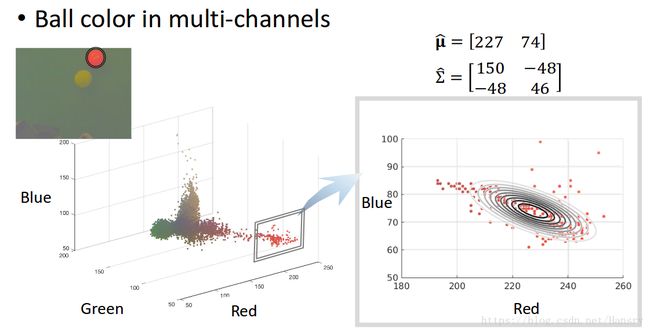
回到小球的例子，我们可以得到其更加具体的分布，如下图所示，红色和蓝色随机变量呈现的是负相关关系。

5. 高斯混合模型（Gaussians mixture model， GMM）

高斯混合模型的优点和缺点？
如何从数学上描述高斯混合模型？

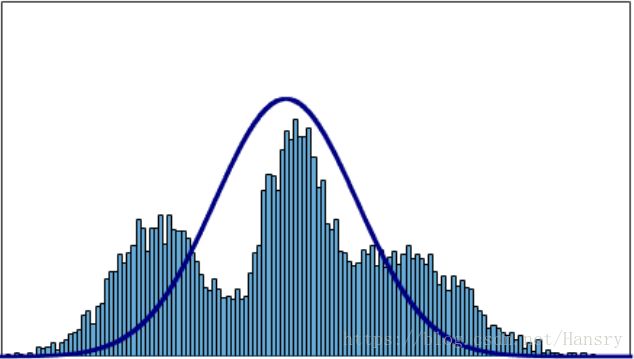
在实际中，一个随机变量的分布不一定是只有一个峰值且对称的，这时候我们可以用多个高斯分布来代表这样一个随机变量的分布。若只用一个高斯分布来表示，则结果可能不会满意，如下图所示：

多个高斯分布相加得到一个新的分布:

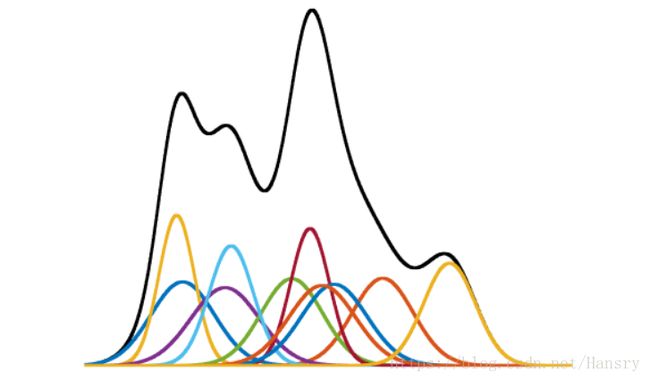
首先，我们令 g 代表一个有某均值和协方差的单纯高斯模型的密度函数，则混合高斯模型（GMM）可以被写成：

$p(x)={\sum }_{k=1}^K{w}_k{g}_k(x|u_k,{\sum }_k)$,

其中 $g_k(x|u_k,{\sum }_k)$代表参数为$({\mu }_k,{\sum }_k)$的单纯高斯分布。

混合高斯模型由这些有不同参数的高斯模型的加权求和，其中 $w_k$都是正的，且他们的和为1，即${\sum }_{k=1}^K{w}_k=1,w_k>0。$

这保证了混合高斯模型的密度函数积分仍然为1，理论上可以用多个高斯分布表示任意形状的分布。

但是混合高斯模型也有以下的缺点：

1. 参数变多：
   $\mu =\left\{\begin{array}{c}{\mu }_1,{\mu }_2,...,{\mu }_k\end{array}\right\}$
   $\sum =\left\{\begin{array}{c}{\sum }_1,{\sum }_2,...,{\sum }_k\end{array}\right\}$
   $\mathbf{w}$
   $\mathbf{K}$
2. 参数没有解析解
3. 过拟合

6. 利用期望最大化算法估计混合高斯模型参数（GMM Parameter Estimation via EM）

不同于纯高斯模型，对于混合高斯模型，我们很难求出令人满意的解析解（analytics solution）。相反，通过期望最大化迭代算法（Expectation Maximization）可以得到局部的优化解。

純高斯模型只有俩个参数，$u$ 和 $\sum$, 而混合高斯模型多个$\mu$、$\sum$、$w$ 和 高斯模型的个数 $K$。

在接下来的计算中，我们令$w=\frac{1}{K}$，这可以让我们把重心放在怎样估计均值和方差矩阵的参数。

简单回顾一下，最大似然估计（maximum likelihood estimation）意味着我们要寻找模型的参数来使得模型最可能产生观察到的数据。

对于最大似然估计，从前面可得：
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
$$\begin{gathered} \hat{\mu },\hat{\Sigma } \\ =arg\underset{\mu ,\Sigma }{\max }{\prod }_{i=1}^{N}p(x_i|\mu ,\Sigma ) \\ =arg\underset{\mu ,\Sigma }{\max }ln\left\{\begin{array}{c}{\prod }_{i=1}^{N}p(x_i|\mu ,\Sigma )\end{array}\right\} \\ =arg\underset{\mu ,\Sigma }{\max }{\sum }_{i=1}^{N}lnp(x_i|\mu ,\Sigma ) \end{gathered}$$
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
由于 $p(x)={\sum }_{k=1}^K{w}_k{g}_k(x|u_k,{\sum }_k)$

故得到：$\hat{\mu },\hat{\Sigma }=arg\underset{\mu ,\Sigma }{\max }{\sum }_{i=1}^{N}ln\left\{\begin{array}{c}\frac{1}{K}{\sum }_{k=1}^K{g}_k(x_i|u_k,{\Sigma }_k)\end{array}\right\}$ (不能再继续简化了，因为在log函数中对純高斯模型进行了求和，所以不能通过求导来求得最小值)。

在特定的条件下，我们可以通过EM算法来得到合理的结果，首先就求解高斯混合模型（GMM）参数，引入EM。

1. 对$\mu 、\Sigma$进行初始化猜测。
2. 新的变量$Z$，我们称之为潜在变量（latent variable）

**首先我们需要先估计需要求解的参数。**对于这类非凸优化(non-convex optimization)的复杂问题,有许多的次优解（suboptimal solutions），我们称之为局部最小值（local minimum）。同时，初始化的值将会影响到最后的结果，因此初始值对该问题而言是十分重要的。

接着我们讨论潜在变量 $Z$。潜在变量Z为关于第K个高斯模型的第$i$个数据点的潜在变量，定义为第k个高斯模型在该数据点处的相对比。本质上，$Z$表明了第i个点是由第k个高斯模型产生的概率。 表达如下：

$z_k^i=\frac{g_k(x_i|u_k,{\Sigma }_k)}{{\sum }_{k=1}^K{g}_k(x_i|u_k,{\Sigma }_{k}g)}$

让我们来探讨下在1维情况下的例子，其中K=2。在一维情况下，我们有一系列点，其中有俩个高斯模型g1和g2，且g1在$x_i$处的概率为$p_1$, g2在$x_i$处的概率为$p_2$， 则我们可以计算$z_1^i$和$z_2^i$， 分别代表在第i点中，属于g1和g2模型的概率。

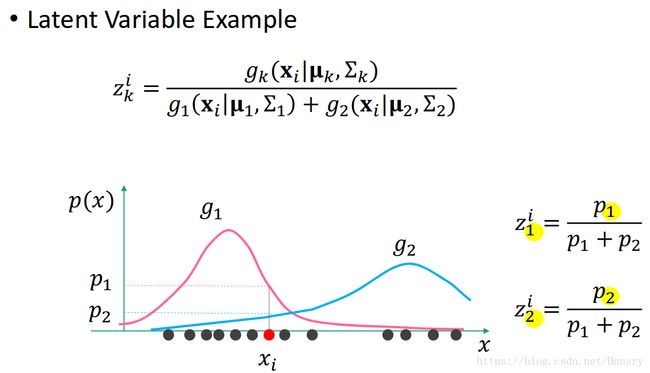
现在，给定所有数据点关于所有模型的潜在变量，我们可以重新定义带权的均值和协方差矩阵，该权重指的是Z。如果一个数据点属于第k个高斯模型的概率很小，则这个点对计算第k个模型的参数的贡献就越小。

=============================================================
${\hat{\mathbf{u}}}_k=\frac{1}{z_k}{\sum }_{i=1}^N{z}_k^i{\mathbf{x}}_i$
${\hat{\mathbf{\Sigma }}}_k=\frac{1}{z_k}{\sum }_{i=1}^N{z}_k^i{({\mathbf{x}}_{\mathbf{i}}-\widehat{{\mathbf{u}}_{\mathbf{k}}})({\mathbf{x}}_{\mathbf{i}}-{\hat{\mathbf{u}}}_{\mathbf{k}})}^T$
$z_k={\sum }_{i=1}^N{z}_k^i$ (这三条公式说明怎么通过潜在变量Z来更新$\mu$ 和 $\Sigma$)

综合之前讨论的东西，我们可以迭代的计算参数和潜在变量，直到其值收敛为止。以下是计算的步骤：
1.初始化参数$\mu 、\Sigma$。
2. 使用初始化的参数$\mu 、\Sigma$来计算潜在变量Z。
3. 一旦Z被更新，我们就保持Z不变用来更新$\mu \Sigma$。
4. 重复2.3步，直到参数的改变量变得很小为止。

7. 期望最大化（Expectation Maximization）

需要有一定的概率和凸优化基础。

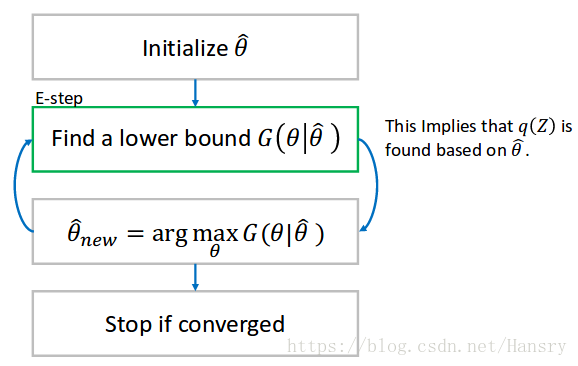
让我们把EM算法看作是对目标函数下界的最大化过程。

EM算法的主要思想可以用 Jensen 不等式解释，考虑一个如下图的2维图所示的凸函数，我们在定义域中取俩点$x_1$和$x_2$以及他们的中点$\frac{x_1+x_2}{2}$。

现在我们将比较俩个值，首先是中点的函数值 $f(\frac{x_1+x_2}{2})$, 是曲线上的一个点，第二个是俩点函数值的平均值 $\frac{f(x_1)+f(x_2)}{2}$, 落在$f{x}_1$ 和$f{x}_2$ 俩个点的连线上。

可以清楚的看到，直线在函数曲线的上方，因此$\frac{f(x_1)+f(x_2)}{2}$ 永远大于$f(\frac{x_1+x_2}{2})$。

我们可以一般化这个想法，$f(a_1{x}_1+a_2{x}_2)⩽a_{1}f(x_1)+a_{2}f(x_2)$, 这个不等式在任意大于0的权值下都成立。其中 $a_1+a_2=1,a_1⩾0,a_2⩾0$。

事实上，它同样适用于正权值下多个点的情况，可得$f(\sum a_i{x}_i)⩽\sum a_{i}f(x_i)$, 其中 $\sum a_i=1,a_i⩾0$。

甚至在多维的情况下，只要我们的函数是凸的。如果函数是凹的，我们只需要翻转这个函数，即$f(\sum a_i{x}_i)⩾\sum a_{i}f(x_i)$。

由于我们接下来要处理的是对数函数，且它是凹函数，故有
$（1）ln(\sum a_i{x}_i)⩾\sum a_{i}ln{x}_i$。

现在我们引入我们永远都无法确切知道的潜在变量（latent variable），潜在变量在一些特定的应用中是清楚的，例如前面提到的混合高斯模型的参数估计。我们需要在所有变量上取潜在变量的边缘概率（What we are going to do with this latent variable is to take the marginal probability over the variable）。

$（2）p(X|\theta )={\sum }_{Z}p(X,Z|\theta )$

在之前，我们考虑概率的对数:
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
$$\begin{gathered} lnp(X|\theta ) \\ =ln{\sum }_{Z}p(X,Z|\theta )(对数形式的似然,log-likelihood) \\ =ln{\sum }_{Z}q(Z)\frac{p(X,Z|\theta )}{q(Z)}(q(Z)是Z有效的概率分布) \\ ⩾{\sum }_{Z}q(Z)ln\frac{p(X,Z|\theta )}{q(Z)}(下界,lowerbound) \end{gathered}$$
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

正如我们无法直接最大化概率和的对数，但是我们可以利用函数的下界，对于它我们是可以计算的。获得下界意味着找到了潜在变量（latent variable） Z的一个分布$q(Z)$。

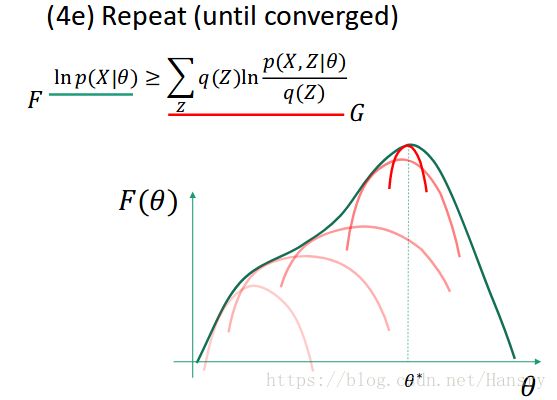
假设我们有一个初始猜测的参数 ${\theta }_0$,并且我们通过利用猜测的参数 ${\theta }_0$得到了 $q$, 进而得到了下界 $g$。

$3(a) \ ln \ p(X|\theta) \geqslant \ \sum_{Z} q(Z) \ ln \ \frac{p(X,Z|\theta)}{q(Z)} $

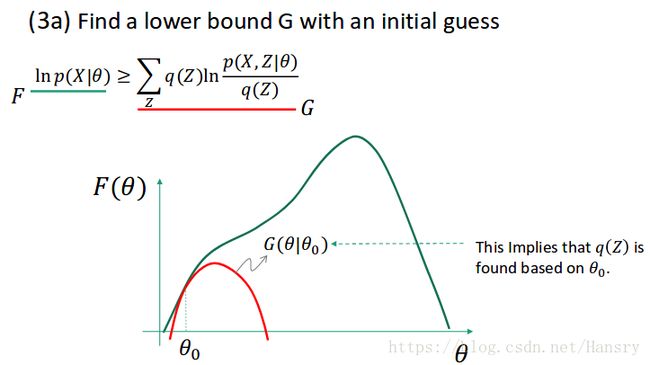
正如前面提到的，对数形式的概率可以被看做是参数的函数。假设f 和 g 是如图所示的 $\theta$ 的函数，f 和 g并不一样，但是它们在 ${\theta }_0$ 附件有一些局部的相似性。别忘记我们是要求一个参数的最大似然估计，给定下界G，我们可以找到一个更好的参数${\theta }^{\ast }$, 这仍然不是F的最大值，但是它比之前的估计更优。

由于找到了${\theta }^{\ast }$,我们可以更新$\theta$ 的值，再重新找到新的下界，通过下界，通过求出下界的最大值是后的参数$\theta$ 进而又再次求出${\theta }^{\ast }$。

不断更新，最后收敛为止：

所以，EM 算法是一个相当强大的算法，其算法流程如下所示：