基于Problem Solving with Algorithms and Data Structures using Python的学习记录（5）——Searching

5.1.目标

• 能够解释和实现顺序查找和二分查找。
• 能够解释和实现选择排序，冒泡排序，归并排序，快速排序，插入排序和 shell 排序。
• 理解哈希作为搜索技术的思想。
• 引入映射抽象数据类型。
• 使用哈希实现 Map 抽象数据类型。

5.2.搜索

我们现在把注意力转向计算中经常出现的一些问题，即搜索和排序问题。在本节中，我们将研究搜索。我们将在本章后面的章节中介绍。搜索是在项集合中查找特定项的算法过程。搜索通常对于项是否存在返回 True 或 False。有时它可能返回项被找到的地方。我们在这里将仅关注成员是否存在这个问题。

在 Python 中，有一个非常简单的方法来询问一个项是否在一个项列表中。我们使用 in 运算符。

>>> 15 in [3,5,2,4,1]
False
>>> 3 in [3,5,2,4,1]
True
>>>

这很容易写，一个底层的操作替我们完成这个工作。事实证明，有很多不同的方法来搜索。我们在这里感兴趣的是这些算法如何工作以及它们如何相互比较。

5.3.顺序查找

当数据项存储在诸如列表的集合中时，我们说它们具有线性或顺序关系。 每个数据项都存储在相对于其他数据项的位置。 在 Python 列表中，这些相对位置是单个项的索引值。由于这些索引值是有序的，我们可以按顺序访问它们。 这个过程产生我们的第一种搜索技术 顺序查找。

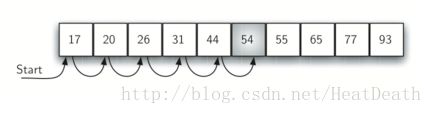
Figure 1 展示了这种搜索的工作原理。 从列表中的第一个项目开始，我们按照基本的顺序排序，简单地从一个项移动到另一个项，直到找到我们正在寻找的项或遍历完整个列表。如果我们遍历完整个列表，则说明正在搜索的项不存在。

该算法的 Python 实现见 CodeLens 1。该函数需要一个列表和我们正在寻找的项作为参数，并返回一个是否存在的布尔值。found 布尔变量初始化为 False，如果我们发现列表中的项，则赋值为 True。

def sequentialSearch(alist, item):
    pos = 0
    found = False

    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True

        else:
            pos = pos + 1

    return found

testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]

print(sequentialSearch(testlist, 3))

print(sequentialSearch(testlist, 0))

5.3.1.顺序查找分析

为了分析搜索算法，我们需要定一个基本计算单位。回想一下，这通常是为了解决问题要重复的共同步骤。对于搜索，计算比较操作数是有意义的。每个比较都有可能找到我们正在寻找的项目。此外，我们在这里做另一个假设。项列表不以任何方式排序。项随机放置到列表中。换句话说，项在列表任何位置的概率是一样的。
如果项不在列表中，知道它的唯一方法是将其与存在的每个项进行比较。如果有n 个项，则顺序查找需要 n 个比较来发现项不存在。在项在列表中的情况下，分析不是那么简单。实际上有三种不同的情况可能发生。在最好的情况下，我们在列表的开头找到所需的项，只需要一个比较。在最坏的情况下，我们直到最后的比较才找到项，第 n 个比较。

平均情况怎么样？平均来说，我们会在列表的一半找到该项; 也就是说，我们将比较 n/2 项。然而，回想一下，当 n 变大时，系数，无论它们是什么，在我们的近似中变得不重要，因此顺序查找的复杂度是 O(n)。Table 1 总结了这些结果。

我们之前假设，我们列表中的项是随机放置的，因此在项之间没有相对顺序。如果项以某种方式排序，顺序查找会发生什么？我们能够在搜索技术中取得更好的效率吗？

假设项的列表按升序排列。如果我们正在寻找的项存在于列表中，它在 n 个位置中的概率依旧相同。我们仍然会有相同数量的比较来找到该项。然而，如果该项不存在，则有一些优点。Figure 2 展示了这个过程，寻找项 50。注意，项仍然按顺序进行比较直到 54。此时，我们知道一些额外的东西。不仅 54 不是我们正在寻找的项，也没有超过 54 的其他元素可以匹配到该项，因为列表是有序的。在这种情况下，算法不必继续查看所有项。它可以立即停止。 CodeLens 2 展示了顺序查找功能的这种变化。

def orderedSequentialSearch(alist, item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos] > item:
                stop = True
            else:
                pos = pos + 1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42]

print(orderedSequentialSearch(testlist, 40))

print(orderedSequentialSearch(testlist, 32))

Table 2 总结了这些结果。 请注意，在最好的情况下，我们通过只查看一项会发现该项不在列表中。 平均来说，我们将只了解 n/2 项就知道。然而，这种复杂度仍然是 O(n)。 总之，只有在我们没有找到该项的情况下，才通过对列表排序来改进顺序查找。

5.4.二分查找

有序列表对于我们的比较是很有用的。在顺序查找中，当我们与第一个项进行比较时，如果第一个项不是我们要查找的，则最多还有 n-1 个项目。 二分查找从中间项开始，而不是按顺序查找列表。 如果该项是我们正在寻找的项，我们就完成了查找。 如果它不是，我们可以使用列表的有序性质来消除剩余项的一半。如果我们正在查找的项大于中间项，就可以消除中间项以及比中间项小的一半元素。如果该项在列表中，肯定在大的那半部分。

然后我们可以用大的半部分重复这个过程。从中间项开始，将其与我们正在寻找的内容进行比较。再次，我们找到元素或将列表分成两半，消除可能的搜索空间的另一部分。Figure 3 展示了该算法如何快速找到值 54 。完整的函数见CodeLens 3中。

def binarySearch(alist, item):
    first = 0
    last = len(alist) - 1
    found = False

    while first <= last and not found:
        midpoint = (first + last) // 2
        if alist[midpoint] == item:
            found = True

        else:
            if item < alist[midpoint]:
                last = midpoint - 1

            else:
                first = midpoint + 1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]

print(binarySearch(testlist, 3))

print(binarySearch(testlist, 13))

在我们继续分析之前，我们应该注意到，这个算法是分而治之策略的一个很好的例子。分和治意味着我们将问题分成更小的部分，以某种方式解决更小的部分，然后重新组合整个问题以获得结果。 当我们执行列表的二分查找时，我们首先检查中间项。如果我们正在搜索的项小于中间项，我们可以简单地对原始列表的左半部分执行二分查找。同样，如果项大，我们可以执行右半部分的二分查找。 无论哪种方式，都是递归调用二分查找函数。 CodeLens 4 展示了这个递归版本。

def binarySearch(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist) // 2
        if alist[midpoint] == item:
            return True
        else:
            if item < alist[midpoint]:
                return binarySearch(alist[:midpoint], item)

            else:
                return binarySearch(alist[midpoint:1], item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]

print(binarySearch(testlist, 3))

print(binarySearch(testlist, 13))

5.4.1.二分查找分析

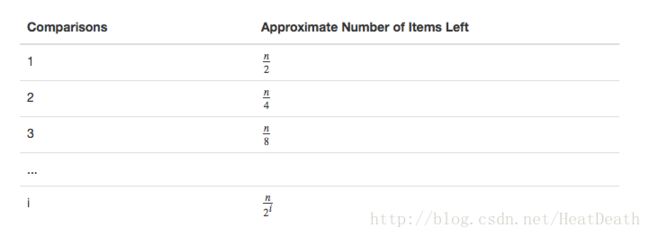
为了分析二分查找算法，我们需要记住，每个比较消除了大约一半的剩余项。该算法检查整个列表的最大比较数是多少？如果我们从 n 项开始，大约 n/2 项将在第一次比较后留下。第二次比较后，会有约 n/4。 然后 n/8，n/16，等等。 我们可以拆分列表多少次？ Table 3 帮助我们找到答案。

当我们切分列表足够多次时，我们最终得到只有一个项的列表。 要么是我们正在寻找的项，要么不是。达到这一点所需的比较数是 i，当 n/2^i = 1 时。 求解 i 得出 i = log^n 。 最大比较数相对于列表中的项是对数的。 因此，二分查找是 O( log^n )。

还需要解决一个额外的分析问题。在上面所示的递归解中，递归调用，

binarySearch(alist[:midpoint],item)

使用切片运算符创建列表的左半部分，然后传递到下一个调用（同样对于右半部分）。我们上面做的分析假设切片操作符是恒定时间的。然而，我们知道 Python中的 slice 运算符实际上是 O(k)。这意味着使用 slice 的二分查找将不会在严格的对数时间执行。幸运的是，这可以通过传递列表连同开始和结束索引来纠正。可以像 CodeLens 3 中所做的那样计算索引。我们将此实现作为练习。

即使二分查找通常比顺序查找更好，但重要的是要注意，对于小的 n 值，排序的额外成本可能不值得。事实上，我们应该经常考虑采取额外的分类工作是否使搜索获得好处。如果我们可以排序一次，然后查找多次，排序的成本就不那么重要。然而，对于大型列表，一次排序可能是非常昂贵，从一开始就执行顺序查找可能是最好的选择。

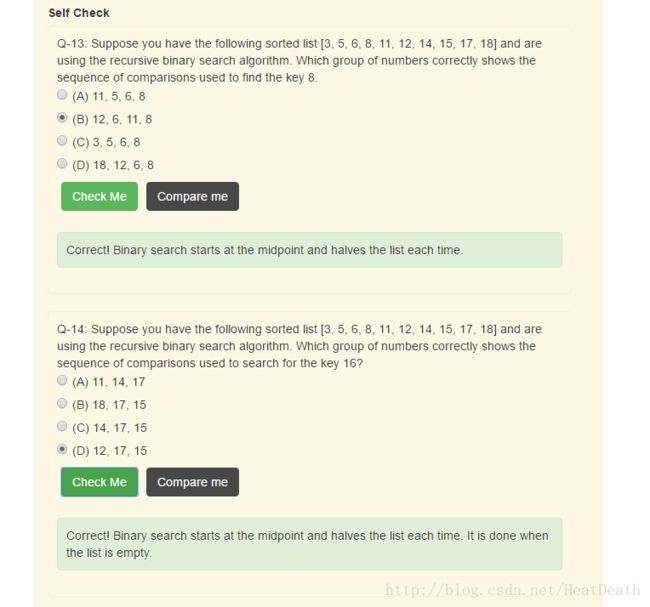
Check Yourself

5.5.Hash查找

在前面的部分中，我们通过利用关于项在集合中相对于彼此存储的位置的信息，改进我们的搜索算法。例如，通过知道列表是有序的，我们可以使用二分查找在对数时间中搜索。在本节中，我们将尝试进一步建立一个可以在 O(1) 时间内搜索的数据结构。这个概念被称为 Hash 查找。

为了做到这一点，当我们在集合中查找项时，我们需要更多地了解项可能在哪里。如果每个项都在应该在的地方，那么搜索可以使用单个比较就能发现项的存在。然而，我们看到，通常不是这样的。

哈希表 是以一种容易找到它们的方式存储的项的集合。哈希表的每个位置，通常称为一个槽，可以容纳一个项，并且由从 0 开始的整数值命名。例如，我们有一个名为 0 的槽，名为 1 的槽，名为 2 的槽，以上。最初，哈希表不包含项，因此每个槽都为空。我们可以通过使用列表来实现一个哈希表，每个元素初始化为None 。Figure 4 展示了大小 m = 11 的哈希表。换句话说，在表中有 m 个槽，命名为 0 到 10。

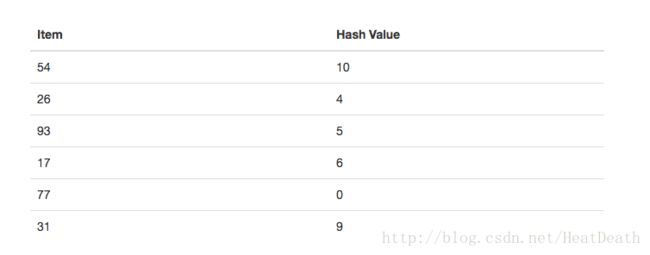
项和该项在散列表中所属的槽之间的映射被称为 hash 函数。 hash 函数将接收集合中的任何项，并在槽名范围内（0和 m-1之间）返回一个整数。假设我们有整数项 54,26,93,17,77 和 31 的集合。我们的第一个 hash 函数，有时被称为 余数法 ，只需要一个项并将其除以表大小，返回剩余部分作为其散列值（h(item) = item％11）。 Table 4 给出了我们的示例项的所有哈希值。注意，这种余数方法（模运算）通常以某种形式存在于所有散列函数中，因为结果必须在槽名的范围内。

一旦计算了哈希值，我们可以将每个项插入到指定位置的哈希表中，如 Figure 5 所示。注意，11 个插槽中的 6 个现在已被占用。这被称为负载因子，通常表示为 λ=项数/表大小, 在这个例子中，λ = 6/11 。

现在，当我们要搜索一个项时，我们只需使用哈希函数来计算项的槽名称，然后检查哈希表以查看它是否存在。该搜索操作是 O(1)，因为需要恒定的时间量来计算散列值，然后在该位置索引散列表。如果一切都正确的话，我们已经找到了一个恒定时间搜索算法。

你可能已经看到，只有每个项映射到哈希表中的唯一位置，这种技术才会起作用。 例如，如果项 44 是我们集合中的下一个项，则它的散列值为0（44％11 == 0）。 因为 77 的哈希值也是 0，我们会有一个问题。根据散列函数，两个或更多项将需要在同一槽中。这种现象被称为碰撞（它也可以被称为“冲突”）。显然，冲突使散列技术产生了问题。我们将在后面详细讨论。

5.5.1.hash 函数

给定项的集合，将每个项映射到唯一槽的散列函数被称为完美散列函数。如果我们知道项和集合将永远不会改变，那么可以构造一个完美的散列函数。不幸的是，给定任意的项集合，没有系统的方法来构建完美的散列函数。幸运的是，我们不需要散列函数是完美的，仍然可以提高性能。

总是具有完美散列函数的一种方式是增加散列表的大小，使得可以容纳项范围中的每个可能值。这保证每个项将具有唯一的槽。虽然这对于小数目的项是实用的，但是当可能项的数目大时是不可行的。例如，如果项是九位数的社保号码，则此方法将需要大约十亿个槽。如果我们只想存储 25 名学生的数据，我们将浪费大量的内存。

我们的目标是创建一个散列函数，最大限度地减少冲突数，易于计算，并均匀分布在哈希表中的项。有很多常用的方法来扩展简单余数法。我们将在这里介绍其中几个。

分组求和法 将项划分为相等大小的块（最后一块可能不是相等大小）。然后将这些块加在一起以求出散列值。例如，如果我们的项是电话号码 436-555-4601，我们将取出数字，并将它们分成2位数（43,65,55,46,01）。43 + 65 + 55 + 46 + 01，我们得到 210。我们假设哈希表有 11 个槽，那么我们需要除以 11 。在这种情况下，210％11 为 1，因此电话号码 436-555-4601 散列到槽 1 。一些分组求和法会在求和之前每隔一个反转。对于上述示例，我们得到 43 + 56 + 55 + 64 + 01 = 219，其给出 219％11 = 10 。

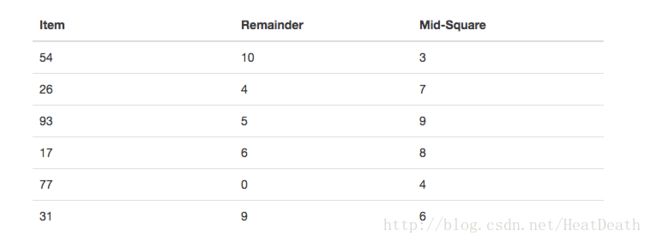
用于构造散列函数的另一数值技术被称为 平方取中法。我们首先对该项平方，然后提取一部分数字结果。例如，如果项是 44，我们将首先计算 44^2 = 1,936 。通过提取中间两个数字 93 ，我们得到 5（93％11）。Table 5 展示了余数法和中间平方法下的项。

我们还可以为基于字符的项（如字符串）创建哈希函数。 词 cat 可以被认为是 ascii 值的序列。

>>> ord('c')
99
>>> ord('a')
97
>>> ord('t')
116

然后，我们可以获取这三个 ascii 值，将它们相加，并使用余数方法获取散列值（参见 Figure 6）。 Listing 1 展示了一个名为 hash 的函数，它接收字符串和表大小 作为参数，并返回从 0 到 tablesize-1 的范围内的散列值。

你可以思考一些其他方法来计算集合中项的散列值。重要的是要记住，哈希函数必须是高效的，以便它不会成为存储和搜索过程的主要部分。如果哈希函数太复杂，则计算槽名称的程序要比之前所述的简单地进行基本的顺序或二分搜索更耗时。 这将打破散列的目的。

5.5.2.冲突解决

我们现在回到碰撞的问题。当两个项散列到同一个槽时，我们必须有一个系统的方法将第二个项放在散列表中。这个过程称为冲突解决。如前所述，如果散列函数是完美的，冲突将永远不会发生。然而，由于这通常是不可能的，所以冲突解决成为散列非常重要的部分。

解决冲突的一种方法是查找散列表，尝试查找到另一个空槽以保存导致冲突的项。一个简单的方法是从原始哈希值位置开始，然后以顺序方式移动槽，直到遇到第一个空槽。注意，我们可能需要回到第一个槽（循环）以查找整个散列表。这种冲突解决过程被称为开放寻址，因为它试图在散列表中找到下一个空槽或地址。通过系统地一次访问每个槽，我们执行称为线性探测的开放寻址技术。

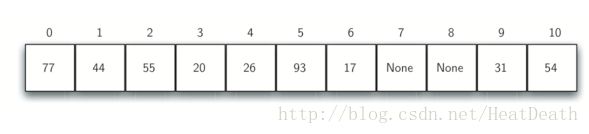
Figure 8展示了在简单余数法散列函数（54,26,93,17,77,31,44,55,20） 下的整数项的扩展集合。上面的 Table 4 展示了原始项的哈希值。Figure 5 展示了原始内容。当我们尝试将 44 放入槽 0 时，发生冲突。在线性探测下，我们逐个顺序观察，直到找到位置。在这种情况下，我们找到槽 1。

再次，55 应该在槽 0 中，但是必须放置在槽 2 中，因为它是下一个开放位置。值 20 散列到槽 9 。由于槽 9 已满，我们进行线性探测。我们访问槽10,0,1和 2，最后在位置 3 找到一个空槽。

一旦我们使用开放寻址和线性探测建立了哈希表，我们就必须使用相同的方法来搜索项。假设我们想查找项 93 。当我们计算哈希值时，我们得到 5 。查看槽 5 得到 93，返回 True。如果我们正在寻找 20， 现在哈希值为 9，而槽 9 当前项为 31 。我们不能简单地返回 False，因为我们知道可能存在冲突。我们现在被迫做一个顺序搜索，从位置 10 开始寻找，直到我们找到项 20 或我们找到一个空槽。

线性探测的缺点是聚集的趋势;项在表中聚集。这意味着如果在相同的散列值处发生很多冲突，则将通过线性探测来填充多个周边槽。这将影响正在插入的其他项，正如我们尝试添加上面的项 20 时看到的。必须跳过一组值为 0 的值，最终找到开放位置。该聚集如 Figure 9 所示。

处理聚集的一种方式是扩展线性探测技术，使得不是顺序地查找下一个开放槽，而是跳过槽，从而更均匀地分布已经引起冲突的项。这将潜在地减少发生的聚集。 Figure 10 展示了使用 加3 探头进行碰撞识别时的项。 这意味着一旦发生碰撞，我们将查看第三个槽，直到找到一个空。

在冲突后寻找另一个槽的过程叫重新散列。使用简单的线性探测，rehash 函数是 newhashvalue = rehash(oldhashvalue)其中 rehash(pos)=(pos + 1)％sizeoftable。 加3rehash 可以定义为rehash(pos)=(pos + 3)％sizeoftable。一般来说，rehash(pos)=(pos + skip)％sizeoftable。重要的是要注意，“跳过”的大小必须使得表中的所有槽最终都被访问。否则，表的一部分将不被使用。为了确保这一点，通常建议表大小是素数。这是我们在示例中使用 11 的原因。

线性探测思想的一个变种称为二次探测。代替使用常量 “跳过” 值，我们使用rehash 函数，将散列值递增 1，3，5，7，9， 依此类推。这意味着如果第一哈希值是 h，则连续值是h + 1，h + 4，h + 9，h + 16，等等。换句话说，二次探测使用由连续完全正方形组成的跳跃。Figure 11 展示了使用此技术放置之后的示例值。

用于处理冲突问题的替代方法是允许每个槽保持对项的集合（或链）的引用。链接允许许多项存在于哈希表中的相同位置。当发生冲突时，项仍然放在散列表的正确槽中。随着越来越多的项哈希到相同的位置，搜索集合中的项的难度增加。 Figure 12 展示了添加到使用链接解决冲突的散列表时的项。

当我们要搜索一个项时，我们使用散列函数来生成它应该在的槽。由于每个槽都有一个集合，我们使用一种搜索技术来查找该项是否存在。优点是，平均来说，每个槽中可能有更少的项，因此搜索可能更有效。我们将在本节结尾处查看散列的分析。

5.5.3.实现 map 抽象数据类型

最有用的 Python 集合之一是字典。回想一下，字典是一种关联数据类型，你可以在其中存储键-值对。该键用于查找关联的值。我们经常将这个想法称为 map。
map 抽象数据类型定义如下。该结构是键与值之间的关联的无序集合。map 中的键都是唯一的，因此键和值之间存在一对一的关系。操作如下。

• Map() 创建一个新的 map 。它返回一个空的 map 集合。
• put(key，val) 向 map 中添加一个新的键值对。如果键已经在 map 中，那么用新值替换旧值。
• get(key) 给定一个键，返回存储在 map 中的值或 None。
• del 使用 del map[key] 形式的语句从 map 中删除键值对。
• len() 返回存储在 map 中的键值对的数量。
• in 返回 True 对于 key in map 语句，如果给定的键在 map 中，否则为False。

字典一个很大的好处是，给定一个键，我们可以非常快速地查找相关的值。为了提供这种快速查找能力，我们需要一个支持高效搜索的实现。我们可以使用具有顺序或二分查找的列表，但是使用如上所述的哈希表将更好，因为查找哈希表中的项可以接近 O(1) 性能。

在 Listing 2 中，我们使用两个列表来创建一个实现 Map 抽象数据类型的HashTable 类。一个名为 slots 的列表将保存键项，一个称 data 的并行列表将保存数据值。当我们查找一个键时，data 列表中的相应位置将保存相关的数据值。我们将使用前面提出的想法将键列表视为哈希表。注意，哈希表的初始大小已经被选择为 11。尽管这是任意的，但是重要的是，大小是质数，使得冲突解决算法可以尽可能高效。

hash 函数实现简单的余数方法。冲突解决技术是 加1 rehash 函数的线性探测。 put 函数（见 Listing 3）假定最终将有一个空槽，除非 key 已经存在于 self.slots 中。 它计算原始哈希值，如果该槽不为空，则迭代 rehash 函数，直到出现空槽。如果非空槽已经包含 key，则旧数据值将替换为新数据值。

class HashTable:
    def __init__(self):
        # HashTable 的初始大小已经被选择为 11,大小是质数，使得冲突解决算法尽可能的高效
        self.size = 11
        # slots[] 储存key
        self.slots = [None]*self.size
        # data[] 储存value
        self.data = [None]*self.size

    # put 函数,用于给 key-value 找到合适的位置，并将其插入进去
    def put(self, key, data):
        hashvalue = self.hashfunction(key, len(self.slots))

        # 当 hashvalue 对应的槽为空时，将 key 和 data 分别插入 slots[] 和 data[] 中
        if self.slots[hashvalue] == None:
            self.slots[hashvalue] = key
            self.data[hashvalue] =data

        else:
            # 如果非空槽已经包含了 key ，则将以前的 data 替换为新的 data
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data


            else:
                # 使用 rehash() 函数重新计算 hashvalue(nextslot)，即下一个空槽的位置
                nextslot = self.rehash(hashvalue, len(self.slots))

                # 在找到空槽或包含 key 的非空槽之前，迭代 rehash() 函数
                while self.slots[nextslot] != None and self.slots[nextslot] != key:
                    nextslot = self.rehash(nextslot, len(self.slots))

                # 找到空槽，插入 key 和 data
                if self.slots[nextslot] == None:
                    self.slots[nextslot] = key
                    self.data[nextslot] = data

                # 找到包含 key 的非空槽，更新data
                else:
                    self.data[nextslot] = data

    # hashfunction 函数，用于首次计算 hashvalue
    def hashfunction(self, key, size):
        return key % size

    # rehash 函数，用于解决冲突，在发生冲突时再次计算新 hashvalue
    def rehash(self, oldhash, size):
        return (oldhash + 1) % size

同样，get 函数（见 Listing 4）从计算初始哈希值开始。如果值不在初始槽中，则 rehash 用于定位下一个可能的位置。注意，第 15 行保证搜索将通过检查以确保我们没有返回到初始槽来终止。如果发生这种情况，我们已用尽所有可能的槽，并且项不存在。

HashTable 类提供了附加的字典功能。我们重载__getitem__ 和__setitem__方法以允许使用 [] 访问。 这意味着一旦创建了HashTable，索引操作符将可用。

class HashTable:
    def __init__(self):
        # HashTable 的初始大小已经被选择为 11,大小是质数，使得冲突解决算法尽可能的高效
        self.size = 11
        # slots[] 储存key
        self.slots = [None]*self.size
        # data[] 储存value
        self.data = [None]*self.size

    # put 函数,用于给 key-value 找到合适的位置，并将其插入进去
    def put(self, key, data):
        hashvalue = self.hashfunction(key, len(self.slots))

        # 当 hashvalue 对应的槽为空时，将 key 和 data 分别插入 slots[] 和 data[] 中
        if self.slots[hashvalue] == None:
            self.slots[hashvalue] = key
            self.data[hashvalue] =data

        else:
            # 如果非空槽已经包含了 key ，则将以前的 data 替换为新的 data
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data


            else:
                # 使用 rehash() 函数重新计算 hashvalue(nextslot)，即下一个空槽的位置
                nextslot = self.rehash(hashvalue, len(self.slots))

                # 在找到空槽或包含 key 的非空槽之前，迭代 rehash() 函数
                while self.slots[nextslot] != None and self.slots[nextslot] != key:
                    nextslot = self.rehash(nextslot, len(self.slots))

                # 找到空槽，插入 key 和 data
                if self.slots[nextslot] == None:
                    self.slots[nextslot] = key
                    self.data[nextslot] = data

                # 找到包含 key 的非空槽，更新data
                else:
                    self.data[nextslot] = data

    # hashfunction 函数，用于首次计算 hashvalue
    def hashfunction(self, key, size):
        return key % size

    # rehash 函数，用于解决冲突，在发生冲突时再次计算新 hashvalue
    def rehash(self, oldhash, size):
        return (oldhash + 1) % size

    # get函数，用于通过 key 来查找对应的 value
    def get(self, key):

        #使用 hashfunction() 根据 key 来计算查找的起始槽(startslot)
        startslot = self.hashfunction(key, len(self.slots))

        data = None
        stop = False
        found = False
        position = startslot


        while self.slots[position] != None and not found and not stop:

            # 当前槽中的 key 为想要查找的 key 时
            if self.slots[position] == key:
                found = True
                data = self.data[position]

            else:
                position = self.rehash(position, len(self.slots))
                # 当返回起始槽 startsplot 时，终止
                if position == startslot:
                    stop = True

        return data

    # 重载 __getitem__() 和 __stiitem__() 方法，以允许使用[]访问
    # 这意味着一旦创建了 HashTable，索引操作符将可用
    def __getitem__(self, key):
        return  self.get(key)

    def __setitem__(self, key, data):
        return self.put(key, data)

H = HashTable()
H[54] = "cat"
H[26] = "dog"
H[93] = "lion"
H[17] = "tiger"
H[77] = "bird"
H[31] = "cow"
H[44] = "goat"
H[55] = "pig"
H[20] = "chicken"
print(H.slots)
print(H.data)

5.5.4.hash法分析

我们之前说过，在最好的情况下，散列将提供 O(1)，恒定时间搜索。然而，由于冲突，比较的数量通常不是那么简单。即使对散列的完整分析超出了本文的范围，我们可以陈述一些近似搜索项所需的比较数量的已知结果。

我们需要分析散列表的使用的最重要的信息是负载因子 λ。概念上，如果 λ 小，则碰撞的机会较低，这意味着项更可能在它们所属的槽中。如果 λ 大，意味着表正在填满，则存在越来越多的冲突。这意味着冲突解决更困难，需要更多的比较来找到一个空槽。使用链接，增加的碰撞意味着每个链上的项数量增加。

和以前一样，我们将有一个成功的搜索结果和不成功的。对于使用具有线性探测的开放寻址的成功搜索，平均比较数大约为1/2（1 + 1/(1-λ)），不成功的搜索为 1/2(1+(1/1-λ)^2 ) 如果我们使用链接，则对于成功的情况，平均比较数目是 1+λ/2，如果搜索不成功，则简单地是 λ 比较次数。