jzoj3736. 【NOI2014模拟7.11】数学题
Description
Input
输入有多组测例,每组测例有一行,为4 个整数x1,y1, x2, y2,含义见题目描述。输入文件以EOF 结束。
Output
Sample Input
3 0 1 2
6 0 4 0
Sample Output
5
0
Data Constraint
赛时
比赛一眼没啥思路,主要是感觉感冒了,精神状态欠佳。
画画图,瞎**猜了一个神奇的结论:
当两条向量的斜率相同时,答案为0。
当两条向量不相同时,答案就是选择其中一条最短的。
感觉没啥问题,接着去死磕后面的两道毒瘤题了。
比赛即将结束,突然发现结论好像有点问题?
/<_\
题解
我们看看上面我的结论哪里错了——
看到两个夹角等于120°,长度相等的向量。
那么两个向量加起来是等于向量长的。
如果把这个夹角变大点,那么长度就小于向量长了。
所以说,我们要把这类型的情况给做好!
直接上1号结论——当两向量夹角的角度大于60°时,即可利用我的结论。
否则就看到2号结论,再搞搞事情。
证明1号结论:

我直接截取论文上的证明了,还是很好推的(话说论文一开始写错了,那个等于号应该是大于等于)
然后我们来看看2号结论:
∣ a x + b y ∣ = ∣ a ( x − λ y ) + ( b + a λ ) y ∣ |ax+by|=|a(x-\lambda y)+(b+a\lambda)y| ∣ax+by∣=∣a(x−λy)+(b+aλ)y∣,即向量 ( x , y ) (x,y) (x,y)可以转换成 ( x − λ y , y ) (x-\lambda y,y) (x−λy,y),且系数 ( a , b ) (a,b) (a,b)可以转换成系数 ( a , b + a λ ) (a,b+a\lambda) (a,b+aλ)
证明显然。
由于系数这个东西是自己随意确定的。
所以,向量就可以利用上面的东西变成新的向量,同时扩大夹角。
因此在不停地扩大的过程中,夹角也最终会大于60°,回到结论1即可。
那么我们来看看具体如何扩大:
还是论文的图
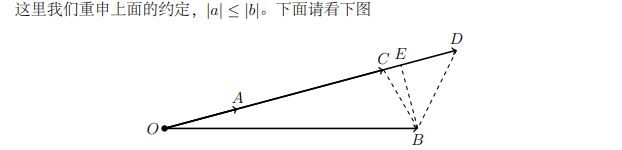
我们设 O E → \overrightarrow {OE} OE为 O B → \overrightarrow {OB} OB在 O A → \overrightarrow {OA} OA上的投影。
那么接下来有3种情况:
1、 ∣ O A → ∣ < ∣ O E → ∣ |\overrightarrow {OA}|<|\overrightarrow {OE}| ∣OA∣<∣OE∣
在这种情况下,也就是上面的图,考虑转化。
设 O C → = λ ∗ O A → \overrightarrow {OC}=\lambda*\overrightarrow {OA} OC=λ∗OA并且其中的 λ \lambda λ在满足 ∣ O C → ∣ < ∣ O E → ∣ |\overrightarrow {OC}|<|\overrightarrow {OE}| ∣OC∣<∣OE∣的情况下 λ \lambda λ最大。
那么现在就可以转化啦。
显然, ∠ D C B > ∠ A O B \angle{DCB}>\angle{AOB} ∠DCB>∠AOB
于是我们就把 ( C B → , O A → ) (\overrightarrow {CB},\overrightarrow {OA}) (CB,OA)代入,继续递归。
2、 ∣ O A → ∣ > ∣ O E → ∣ |\overrightarrow {OA}|>|\overrightarrow {OE}| ∣OA∣>∣OE∣
也就是类似于上面的 O D → \overrightarrow {OD} OD
我们发现, ∠ A D B > ∠ A O B \angle{ADB}>\angle{AOB} ∠ADB>∠AOB,证明的话把D按照E轴对称折叠过去,发现是外角。
把 ( D B → , O A → ) (\overrightarrow {DB},\overrightarrow {OA}) (DB,OA)代入,递归!
3、 ∣ O A → ∣ = ∣ O E → ∣ |\overrightarrow {OA}|=|\overrightarrow {OE}| ∣OA∣=∣OE∣
其实这种情况注意一下即可,写得不正确有可能会死循环。
大致就是这样子,是不是很像gcd算法的过程?这就叫做类欧几里得算法。
一些小细节:
- 如何快速求 λ \lambda λ呢?
λ = ⌊ ∣ O E → ∣ ∣ O A → ∣ ⌋ \lambda=\lfloor \frac{|\overrightarrow {OE}|}{|\overrightarrow {OA}|}\rfloor λ=⌊∣OA∣∣OE∣⌋ - 当递归后夹角大于90°,一样要把一条向量旋转180°。
- 时间复杂度:因为有了上面这条,所以时间复杂度证明变得极其复杂。(其实是我太蔡了)
标程
uses math;
type
nod=record
x,y:extended;
end;
var
i,j,k,l,n,m,anss:longint;
co,kk:extended;
a,b,c:nod;
function jia(a,b:nod):nod;
begin
jia.x:=a.x+b.x;
jia.y:=a.y+b.y;
end;
function jian(a,b:nod):nod;
begin
jian.x:=a.x-b.x;
jian.y:=a.y-b.y;
end;
function cheng(lid:extended;a:nod):nod;
begin
cheng.x:=lid*a.x;
cheng.y:=lid*a.y;
end;
function cross(a,b:nod):extended;
begin
exit(a.x*b.x+a.y*b.y);
end;
function dis(a:nod):extended;
begin
exit(sqrt(a.x*a.x+a.y*a.y));
end;
function ans(a:nod):extended;
begin
exit(a.x*a.x+a.y*a.y);
end;
function likegcd(a,b:nod):extended;
var
c:nod;
det,k:extended;
begin
if (dis(a)>dis(b)) then
begin
c:=a;a:=b;b:=c;
end;
if (dis(a)=0) then
begin
exit(0);
end;
if (dis(b)=0) then
begin
exit(0);
end;
co:=cross(a,b)/(dis(a)*dis(b));
if (co<0) then
begin
a.x:=-a.x;
a.y:=-a.y;
exit(likegcd(a,b));
end;
if (co=1) then
begin
exit(0);
end;
c.x:=b.x*co;
c.y:=b.y*co;
kk:=pi;
if (co<=1/2) then
begin
if (dis(a)>dis(b)) then exit(ans(b))
else exit(ans(a));
end;
if (dis(a)>dis(c)) then
begin
exit(likegcd(jian(b,a),a));
end
else
begin
k:=trunc(dis(c)/dis(a));
exit(likegcd(jian(b,cheng(k,a)),a));
end;
end;
begin
assign(input,'math.in');reset(input);
assign(output,'math.out');rewrite(output);
while not eof do
begin
readln(a.x,a.y,b.x,b.y);
c.x:=-a.x;
c.y:=-a.y;
if dis(jia(c,b))>dis(jia(a,b)) then a:=c;
anss:=trunc(likegcd(a,b));
writeln(anss);
if anss=5584 then
i:=i;
end;
end.

