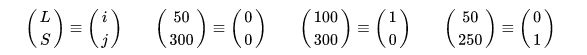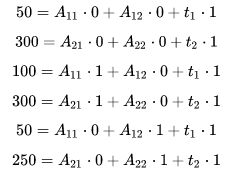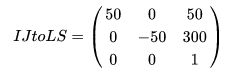3Dslicer中的坐标系统（一）

一、简介

我们在处理医学图像和相关应用时，首先需要我们了解的事情就是不同坐标系统之间的差异，在图像处理应用领域用的比较多比较常见的为以下三种坐标系统：世界坐标系，解刨坐标系和图像坐标系，本文我们主要介绍它们之间的差异和应用。

下图展现三个不同的坐标空间和对应的坐标轴：

                                            三图分别为：世界坐标空间，解刨坐标空间和图像坐标空间

每个坐标系统都有它们的特点和应用方向，并以不同的方式来展现它们的数据。

二、世界坐标系统

世界坐标系统就是典型的笛卡尔坐标系，在这个坐标系中定位了不同的模型（如，一个MRI扫描器，或一个病人）。而每个模型有都有自己的坐标系统，但是世界坐标系只有一个，这样用它可以来确定每个模型的位置和方向。

三、解刨坐标系

对于与医学图像相关的技术来说，最重要的模型坐标系就是解刨坐标空间（也被称为患者坐标系）。这个空间由三个面来组成，依此来描述人体的标准解刨位置：

• 横断面（axial plane）：平行于地面，分割人体的头部（Superior）和脚部（Inferior），上下方向。
• 冠状面（coronal plane）：垂直与地面，分割前部（Anterior）和后部（Posterior），前后方向。
• 矢状面（sagittal plane）：垂直与地面，分割左边（Left）和右边（Right），左右方向。

通过这些平面，空间中的所有轴都有它们的正向描述（S,I,A,P,L,R）,并且这六条轴是反向成三对出现的（S-I,A-P,L-R）.

解刨坐标系是一个三维的连续坐标空间，图像就是在这个坐标空间中进行采样，在神经成像领域，针对人脑部的扫描图像，这个空间经常定义来定位脑部图像。所以，该空间的3D坐标基总是被定义沿着解刨轴A-P S-I, L-R的方向。

然而解刨坐标系的三维坐标基并不总是固定的，不同的医学应用会使用不同的3D坐标基，但坐标基一般遵循右手定则。

• LPS（Left, Posterior, Superior）主要在DICOM图像和ITK 工具箱中被应用
• RAS （Right, Anterior, Superior）与LPS类似，只不过前连个轴进行了反向，被3Dslicer应用。

这两组基同样有用，也同样合乎逻辑，这样我们在进行图像相关操作时，了解图像参考的坐标基就很有必要了。

四、图像坐标系统

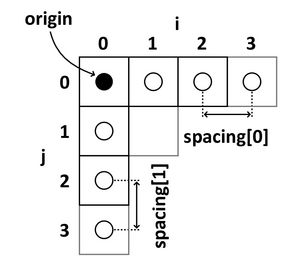
图像坐标系描述了图像是相对解刨结构如何获取的，医学扫描器从左上角开始创建有规律的长方形的点和单元阵列来存储图像信息，i轴向右增长，j轴向底部增长，k轴向后增长。

除了每个体素（i,j,k）的强度值之外，一个完整的图像还应该存储有在解刨系统中，图像的原点和间距信息。

• 原点代表图像中第一个体素(0,0,0)在解刨坐标系统中的位置坐标，e.g. (100mm, 50mm, -25mm)
• 间距指定了体素在每一个轴方向上的间距，e.g. (1.5mm, 0.5mm, 0.5mm)

下面一个二维的示例显示原点和间距的意义：

                                                                    

在知道图像原点和体素间距信息之后，每一个体素对应的解刨空间中的位置坐标就可以被计算出来。

五、图像变换

从图像坐标空间中的一个位置向量（i,j,k）'到解刨坐标空间的一个位置向量x之间的变换使一个仿射变换，由一个线性变换矩阵A和一个平移矩阵t组成。

                                 

线性变换矩阵A是一个3*3的矩阵，包含着所有的空间方向和轴缩放信息。

平移矩阵t是一个3*1的向量，包含着第一个体素的位置信息。

                                            

从该方程可以线性变换由矩阵相乘表示，平移变换由向量相加来表示，为了同时将它们表现出来，故我们可以将这两者通过用一个增广矩阵，以矩阵相乘的方式来表现。这个技术需要将A矩阵增加额外的一行0，再增加额外的一列——即平移矩阵在矩阵右边，用1补在矩阵的右下角。另外所有的向量都写成齐次坐标的形式，即在每个向量的末尾添加1。

                                              

根据采用的解刨空间(LPS or RAS)，该4*4的矩阵称为IJKtoLPS或者IJKtoRAS矩阵，因为它代表了从IJK到LPS或RAS空间的变换。

六、二维示例及计算一个IJtoLS矩阵

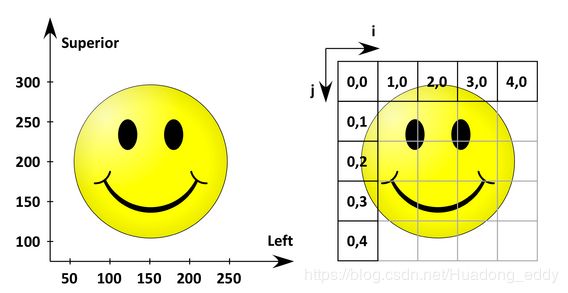
下面的图像，显示了一个图像在以L(P)S为基的解刨空间（左边）和对应的图像坐标空间（右边）

      

图像原点（第一个像素在解刨空间中的位置坐标）为(50 mm, 300 mm) ，间距（两个轴方向上像素间的距离）为(50 mm, 50 mm)

因为这是一个二维的示例，故A为一个2*2的矩阵，t是一个2*1的向量，所以仿射变换的方程为：

                                      

通过将 IJtoLS矩阵和右侧的向量相乘，以下乘积过程会产生：

                                                                     

最后的方程和矩阵乘积总共有六个未知变量要被确定：

                                            

通过已知的原点和间距的信息确定了以下的从图像空间到解刨空间的联系变换：

由此至少可以建立六个方程：

             

上面讲到，平移向量t包含了第一个像素的几何位置信息，等同于坐标原点。该结果求得的六个未知变量也由第一方程式所证实。

所以：