卷积神经网络个人笔记(一)

       这是本人在观看吴恩达老师的关于深度学习课程所作的个人笔记。由于研究生阶段打算进行NLP方面的学习，深度学习也广泛应用于NLP领域。在上完机器学习的网课后，就立马着手学习深度学习相关的知识。这篇是关于卷积神经网络的笔记，参考黄海广博士的相关笔记。

1 边缘检测(基本卷积运算)

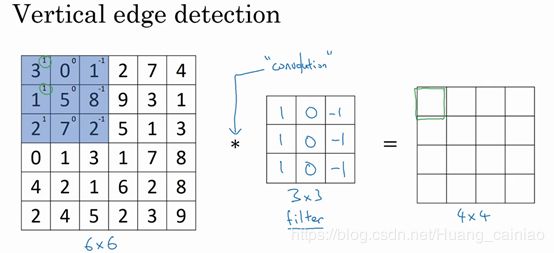
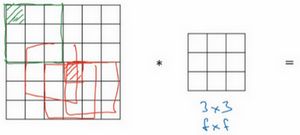
       卷积计算是卷积神经网络中最基本的部分。卷积神经网络在计算机视觉方面有着很好的效果。吴恩达老师从边缘检测开始讲解使大家理解卷积计算。给定一张图片，要计算机判断图片里有什么。可以做的第一件事就是检测图片中的边缘，如下图所示

                                    

       给定一个 6X6的灰度图像，因为是灰度图像，所以为 6X6X1的矩阵。为了检测图像中的垂直边缘，需要构造一个 3X3的矩阵，在神经网络的术语中，该矩阵被称为过滤器(filter)。 该矩阵可以为 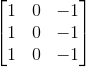 ,在有些论文中，也被称为核。对这个 6x6的图像进行卷积运算,卷积运算用  表示，用 3x3的过滤器对其进行卷积

                                    

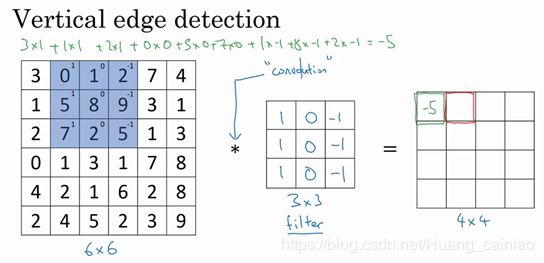
        这个卷积运算会输出一个4x4的矩阵，也可以看作为4x4的图像。4X4矩阵的坐上角的值是由6x6矩阵的左上角的  矩阵与过滤器(也是矩阵) 对应元素相乘后相加所得，如下所示

                                                           

       然后在将矩阵的所有元素相加得到最左的上值，为 -5。接下来4x4矩阵第一行第二个元素的计算为把蓝色的方块（过滤矩阵）向右移动一列,进行上面相同的运算即可。入下图所示

                                  

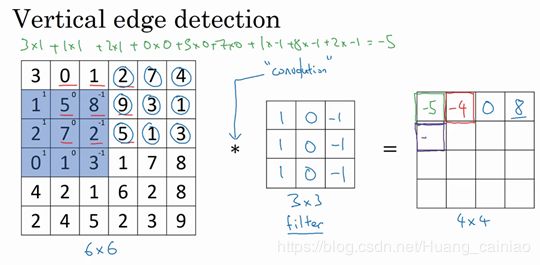
     依照上述方法所计算得出的值为-5。依次计算得出 4x4矩阵的第一行。如果要计算下一行，则将过滤器下移即可，如下图所示

                           

       因此6 x6矩阵和3x3矩阵进行卷积运算得到4x4矩阵。这些图片和过滤其是不同维度的矩阵，左边的矩阵理解为一张图片，中间的图片理解为过滤器，右边的图片可以理解为另一张图片。

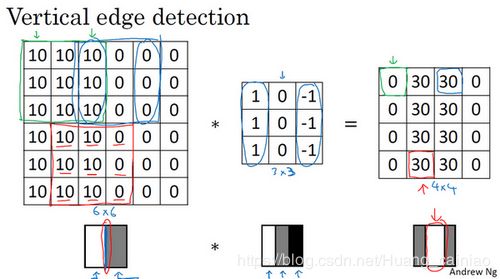
       为什么这样可以进行垂直检测？吴恩达老师举了一个简单的例子，简单的6x6图片，左边一般为10，右边一半为0。如果看成一张图片，那么左边为白色，右边为黑色。图片中有一条明显的垂直边缘在图像中间，这条垂直线是从黑到白的过渡线。如下所示

                                                             

     当你使用一个 3x3的过滤器对上图进行边缘检测，卷积计算后得出的结果如下所示

                                         

    可以看出，中间有一段白色的，这就是我们检测出来的边缘，可能说维数不正确。因为在这个例子中，图片太小了了，如果用一个1000x1000的图片，那么就可以很好的检测出边缘。

   2 更多边缘检测内容

    上图中的例子，左边更亮，右边更暗，是一个从亮到暗的边缘。如果左边更暗，右边更亮，那么使用过滤器计算后会得出

                                    

      可以看出中间的值是-30，这表明是由暗到亮的过程，如果不用区别可以取出矩阵的绝对值，这样就智能检测出边缘。此外，之前的都为检出出垂直边缘，如果我们要检测出水平边缘。可以使用如下的过滤器

                             

      总而言之，通过使用不同的过滤器，你可以找出垂直的或是水平的边缘。但事实上，对于这个3×3的过滤器来说，我们使用了其中的一种数字组合。在计算视觉中，可以使用其他的数字组合

                                

     随着深度学习的发展，我们学习的其中一件事就是当真正的去检测出复杂图像的边缘，不一定要使用论文中所选中的9个数字。把这矩阵中的9个数字当成9个参数，并且在之后你可以学习使用反向传播算法。

  3 Padding

       为了构建深度神经网络，需要学会使用的一个基本卷积操作就是Padding。在之前的例子中，使用3x3的过滤器对6x6进行卷积计算得到4x4的矩阵。因为 3x3 矩阵在 6x6中只有4x4种可能。我们可以得出下面的公式:

        假设有一个 的图像，使用  的过滤器进行卷积，那么输出的维度就是  

     将6与3代入的  ，所以我们输出的是一个 4x4的矩阵。这样的话有两个缺点，第一个缺点就是每次做卷积运算，图像都会缩小，从  缩小到 ，可能再经过几次卷积运算我们的图像就会变得很小了，不能让我们的图像再边缘检测时或者其他特征时变得很小。

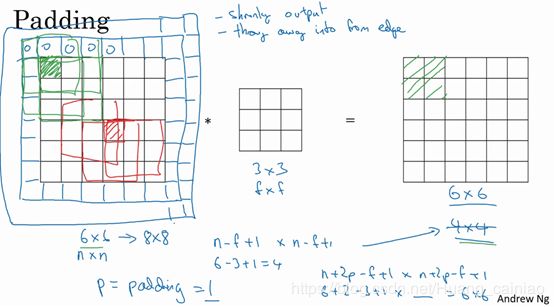
       第二个缺点就是，注意矩阵角落边缘的像素，这些角落处的像素只做过一次计算，也就是输出的值只有一个与之相关。但是如果是中间的像素点，就会经过很多次计算，也就是很多过滤器的区域与之重叠，所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。如下图所示，绿色所代表的就是边缘的像素点，红色代表中间像素点

                                                             

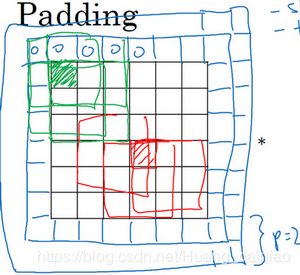
    为解决这两个问题，一是输出缩小，二是丢失图像边缘的大部分信息。我们可以再卷积操作前填充这副图像，如下图所示。

                               

       从图中我们可以看出，在6x6的图像外围再填充一层像素，变成一个 的图像。如果再用 3x3 的过滤器进行卷积那么就会得到一个 6x6 的输出，和原来的图像是一样的。习惯上，我们将所有填充的像素的值都设置为0。之前得出一个公式，由于我们填充了原来的图像，那么我们的公式可以变成

                                                

        p就是我们填充的数量，所以就变成了,和输入的图像一样大。这个涂绿的像素点（左边矩阵）影响了输出中的这些格子（右边矩阵）。这样一来，丢失信息或者更准确来说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

                                                  

        此外还可以选择的大小，如 。至于选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。

       Valid卷积意味着不填充，计算输出的矩阵公式是之前的  。

       另一个经常被用到的填充方法叫做Same卷积，那意味你填充后，你的输出大小和输入大小是一样的。计算输出的矩阵公式是 那么我们可以根据计算得出应该填充多少像素  ,那么可以求出

      ,当  是一个奇数时，填充对应的大小即可，习惯上，计算机视觉中，通常是奇数，甚至可能都是这样。

    4 卷积步长

     卷积中的步幅是另一个构建卷积神经网络的基本操作。我们可以进行如下的操作，用一个的过滤器去卷积一个，按照上面的式子我们输出的得出的是一个 的矩阵。但是如下所示

                                        

      我们得到的输出是一个的矩阵，这是因为我们将步幅也就是卷积步长设置为了 2，如下所示。计算输出矩阵的第一个值还是原来的一样，计算第一行第二个值就是往右移动两步，而不是一步，计算第二行的第一个值就是往下移动2步，如下所示。

                                    

       依次按这样的步骤计算，我们最终得出一个的矩阵。所以在这个例子中，我们使用的矩阵卷积一个 的矩阵。那么输入和输出是由下面的公式决定的。

       如果使用一个的过滤器卷积一个 的图像，你的 padding 为 ，步幅为  ,那么输出的矩阵的大小为

                                         

      如果相除的商不是一个整数，那么我们进行向下取整就好了，因此正确计算输出维度的方法是向下取整，以免不是整数，如下所示

                                          

 5 三维卷积

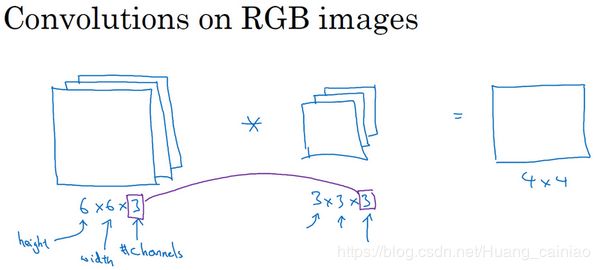
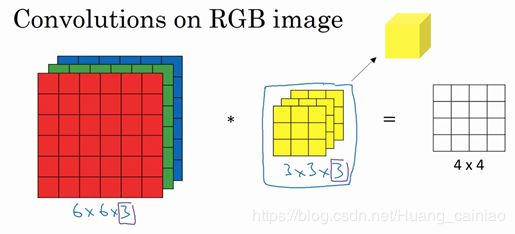
      我们之前的例子都是应用再二维上，卷积同样应用再三维立体上。从一个例子开始说起，假设你不仅想检测灰度图像的特征，也想检测RGB彩色图像的特征。彩色图像如果是6×6×3，这里的3指的是三个颜色通道，你可以把它想象成三个6×6图像的堆叠。为了检测图像的边缘或者其他的特征，不是把它跟原来的3×3的过滤器做卷积，而是跟一个三维的过滤器，它的维度是3×3×3，这样这个过滤器也有三层，对应红绿、蓝三个通道。

                           

       这里的第一个6代表图像高度，第二个6代表宽度，这个3代表通道的数目。同样你的过滤器也有一个高，宽和通道数，并且图像的通道数必须和过滤器的通道数匹配。对三维的卷积如下所示

                                

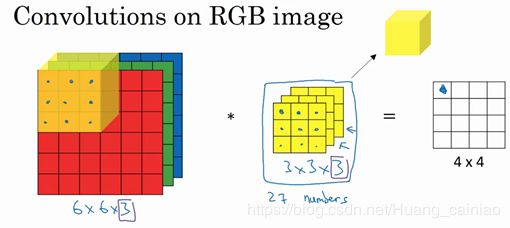
      我们输出的还是一个 4x4的图像，注意是4×4×1，最后一个数不是3了。为了计算这个卷积操作的输出，你要做的就是把这个3×3×3的过滤器先放到最左上角的位置，这个3×3×3的过滤器有27个数，27个参数就是3的立方。依次取这27个数，然后乘以相应的红绿蓝通道中的数字。先取红色通道的前9个数字，然后是绿色通道，然后再是蓝色通道，乘以左边黄色立方体覆盖的对应的27个数，然后把这些数都加起来，就得到了输出的第一个数字。更形象的图如下所示

                                 

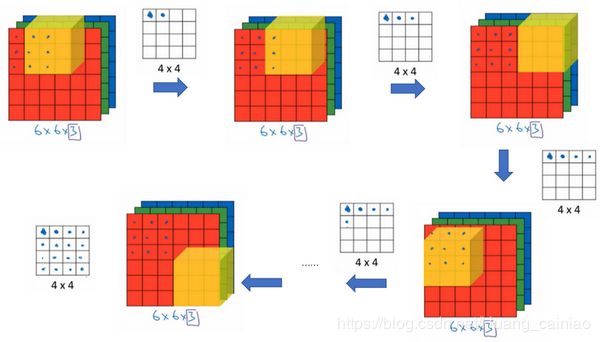
        这和二维的计算并没有什么区别，都是对应元素相乘后相加，只不过在上图中变成计算27个值，剩下的值也就和二维计算的一样向右移动和向下移动

                        

     这个过滤器是3x3x3的，如果像检测红色通道的边缘，我们可以把第一个过滤器设置为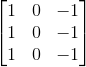,第二个和第三个过滤器都设置为0 ，也就是如果你把这三个堆叠在一起形成一个3×3×3的过滤器，那么这就是一个检测垂直边界的过滤器，但只对红色通道有用。如果不关心边缘出现在哪个颜色通道里，那么可以将三个过滤器都设置为上述第一个过滤器所设置的值。参数的选择不同，你就可以得到不同的特征检测器，所有的都是3×3×3的过滤器。

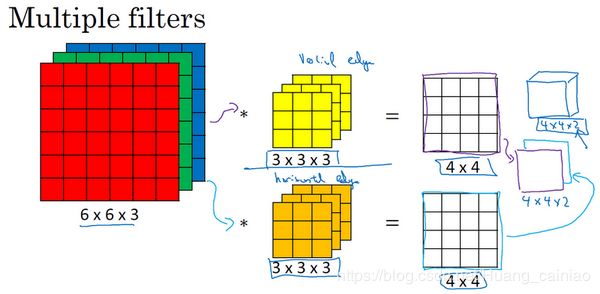
      此外，当我们想要检测不同角度的边缘，例如同时检测垂直边缘和水平边缘，还有45°倾斜的边缘，还有70°倾斜的边缘，那么我们就可以使用多个过滤器，如下所示，第一个过滤器可用作垂直检测，第二个可作为水平检测

                      

       使用多少个检测器都可以，但是注意输出，上图中使用两个检测器，输出为 。我们可以对其进行总结，如果我们有一个  （通道数）的输入图像，在这个例子中为 ,就是通道数，然后使用  进行卷积，那么就得到  (普通卷积),就是我们使用过滤器的个数。

        这个对立方体卷积的概念真的很有用，你现在可以用它的一小部分直接在三个通道的RGB图像上进行操作。更重要的是，你可以检测两个特征，比如垂直和水平边缘或者10个或者128个或者几百个不同的特征，并且输出的通道数会等于你要检测的特征数。