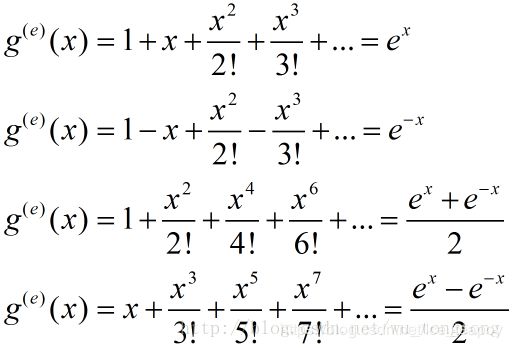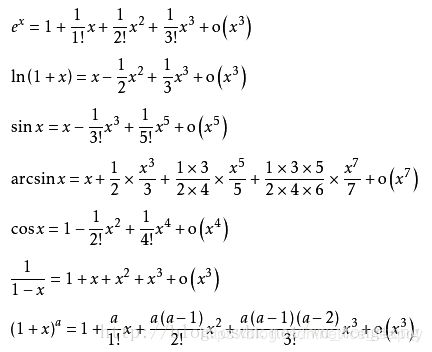数论-生成函数
背景
请鱼块地跳过此项。
生成函数即母函数,是组合数学中尤其是计数方面的一个重要理论和工具。
生成函数有普通型生成函数和指数型生成函数两种,其中普通型用的比较多。形式上说,普通型生成函数用于解决多重集的组合问题,而指数型母函数用于解决多重集的排列问题。
最早提出母函数的人是法国数学家LaplaceP.S.在其1812年出版的《概率的分析理论》中明确提出“生成函数的计算”,书中对生成函数思想奠基人——Euler L在18世纪对自然数的分解与合成的研究做了延伸与发展。生成函数的理论由此基本建立。
生成函数的应用简单来说在于研究未知(通项)数列规律,用这种方法在给出递推式的情况下求出数列的通项,生成函数是推导Fibonacci数列的通项公式方法之一,另外组合数学中的Catalan数也可以通过生成函数的方法得到。
另外生成函数也广泛应用于编程与算法设计、分析上,运用这种数学方法往往对程序效率与速度有很大。<
定义
在数学中某个序列的生成函数(母函数)是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。
使用母函数解决问题的方法称为母函数方法。
生成函数可分为很多种,如普通母函数、指数母函数、L级数、贝尔级数、狄利克雷级数等。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
fib递推式
普通型生成函数
对于数列 { a 0 , a 1 , a 2 . . . a n } \{a_0,a_1,a_2...a_n\} {a0,a1,a2...an},
设 G ( x ) = a 0 + a 1 ∗ x + a 2 ∗ x 2 + a 3 ∗ x 3 + . . . + a n ∗ x n G(x)=a_0+a_1*x+a_2*x^2+a_3*x^3+...+a_n*x^n G(x)=a0+a1∗x+a2∗x2+a3∗x3+...+an∗xn,
则称G(x)是数列的生成函数(generating function)。
一些公式
当 ( x ∈ ( 1 , − 1 ) ) (x∈(1,-1)) (x∈(1,−1))时,
- x 0 + x 2 + x 4 + x 6 . . . = 1 1 − x 2 x^0+x^2+x^4+x^6...=\frac{1}{1−x^2} x0+x2+x4+x6...=1−x21
- 1 ∗ x 0 + 2 ∗ x 1 + 3 ∗ x 2 + 4 ∗ x 3 = 1 ( 1 − x ) 2 1*x^0+2*x^1+3*x^2+4*x^3=\frac{1}{(1-x)^2} 1∗x0+2∗x1+3∗x2+4∗x3=(1−x)21
- ∑ i = 0 ∞ C ( n + i − 1 i ) ∗ x i = 1 ( 1 − x ) n \sum_{i=0}^\infty C(_{n+i-1}^i)*x^i=\frac{1}{(1-x)^n} ∑i=0∞C(n+i−1i)∗xi=(1−x)n1(广义二项式定理)
举个栗子
-
第一个栗子
每一项都是1的无穷数列的生成函数是?
G ( x ) = x 0 + x 1 + x 2 + x 3 + . . . G(x)=x^0+x^1+x^2+x^3+... G(x)=x0+x1+x2+x3+...
= 1 1 − x ( x ∈ ( 1 , − 1 ) ) =\frac{1}{1-x}(x∈(1,-1)) =1−x1(x∈(1,−1))
-
第二个栗子
设n∈N+,数列 { C n 0 , C n 1 , C n 2 , . . . , C n n } \{C_n^0,C_n^1,C_n^2,...,C_n^n\} {Cn0,Cn1,Cn2,...,Cnn}的生成函数是?
G ( x ) = C ( n 0 ) ∗ x 0 + C ( n 1 ) ∗ x 1 + C ( n 2 ) ∗ x 2 + . . . + C ( n n ) ∗ x n = ( x + 1 ) n G(x)=C(_n^0)*x^0+C(_n^1)*x^1+C(_n^2)*x^2+...+C(_n^n)*x^n=(x+1)^n G(x)=C(n0)∗x0+C(n1)∗x1+C(n2)∗x2+...+C(nn)∗xn=(x+1)n
-
第三个栗子
小明有四个盒子,盒子里分别有1,2,3,4块蛋糕。
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。
小明吃了若干块蛋糕。
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
(用生成函数求解)
设生成函数G(x);
指数为蛋糕数,系数为方案数;
对于一个盒子,我们可以选择是否打开:
第一个盒子的方案: ( x 0 + x 1 ) (x^0+x^1) (x0+x1)
第二个盒子的方案: ( x 0 + x 2 ) (x^0+x^2) (x0+x2)
第三个盒子的方案: ( x 0 + x 3 ) (x^0+x^3) (x0+x3)
第四个盒子的方案: ( x 0 + x 4 ) (x^0+x^4) (x0+x4)
四个盒子的开合相互独立;
最终方案 G ( x ) = ( x 0 + x 1 ) ∗ ( x 0 + x 2 ) ∗ ( x 0 + x 3 ) ∗ ( x 0 + x 4 ) G(x)=(x^0+x^1)*(x^0+x^2)*(x^0+x^3)*(x^0+x^4) G(x)=(x0+x1)∗(x0+x2)∗(x0+x3)∗(x0+x4)
= x 0 + x 1 + x 2 + 2 ∗ x 3 + 2 ∗ x 4 + 2 ∗ x 5 + 2 ∗ x 6 + 2 ∗ x 7 + x 8 + x 9 + x 10 =x^0+x^1+x^2+2*x^3+2*x^4+2*x^5+2*x^6+2*x^7+x^8+x^9+x^{10} =x0+x1+x2+2∗x3+2∗x4+2∗x5+2∗x6+2∗x7+x8+x9+x10
我们可以从中得知,小明可能吃到0,1,2,3,4,5,6,7,8,8,10块蛋糕;
有1种方案吃到0块,有1种方案吃到1块,有1种方案吃到2块,有2种方案吃到3块;
有2种方案吃到4块,有2种方案吃到5块,有2种方案吃到6块,有2种方案吃到7块;
有1种方案吃到8块,有1种方案吃到9块,有1种方案吃到10块;
-
第四个栗子
小明有四种盒子,每种盒子有无限个,盒子里分别有1,2,3,4块蛋糕。
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。
小明吃了若干块蛋糕。
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
(用生成函数求解)
设生成函数G(x);
指数为蛋糕数,系数为方案数;
对于一个盒子,我们可以选择打开任意个或不打开:
第一个盒子的方案: ( x 0 + x 1 + x 2 + x 3 + . . . ) (x^0+x^1+x^2+x^3+...) (x0+x1+x2+x3+...)
第二个盒子的方案: ( x 0 + x 2 + x 4 + x 6 + . . . ) (x^0+x^2+x^4+x^6+...) (x0+x2+x4+x6+...)
第三个盒子的方案: ( x 0 + x 3 + x 6 + x 9 + . . . ) (x^0+x^3+x^6+x^9+...) (x0+x3+x6+x9+...)
第四个盒子的方案: ( x 0 + x 4 + x 8 + x 12 + . . . ) (x^0+x^4+x^8+x^{12}+...) (x0+x4+x8+x12+...)
四个盒子的方案相互独立;
最终方案: G ( x ) = ( x 0 + x 1 + x 2 + . . . ) ∗ ( x 0 + x 2 + x 4 + . . . ) ∗ ( x 0 + x 6 + x 6 + . . . ) ∗ ( x 0 + x 4 + x 8 + . . . ) G(x)=(x^0+x^1+x^2+...)*(x^0+x^2+x^4+...)*(x^0+x^6+x^6+...)*(x^0+x^4+x^8+...) G(x)=(x0+x1+x2+...)∗(x0+x2+x4+...)∗(x0+x6+x6+...)∗(x0+x4+x8+...)
我们可以从中得知,小明可能吃了x(x∈N)块蛋糕;
有1种方案吃到0块,有1种方案吃到1块,有2种方案吃到2块,有3种方案吃到3块;
有5种方案吃到4块…
-
第五个栗子
小明有四种盒子,第一种盒子有无限个,每个装有两块蛋糕;第二种盒子有无限个,每个装有五块蛋糕;第三种盒子有四个,每个装有一块蛋糕,第四种盒子有一个,里面装有三块蛋糕。
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。
小明吃了若干块蛋糕。
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
(用生成函数求解)
设生成函数G(x);
指数为蛋糕数,系数为方案数;
对于一个盒子,我们可以选择是否打开:
第一个盒子的方案: ( x 0 + x 2 + x 4 + x 6 + . . . ) (x^0+x^2+x^4+x^6+...) (x0+x2+x4+x6+...)
第二个盒子的方案: ( x 0 + x 5 + x 10 + x 15 + . . . ) (x^0+x^5+x^{10}+x^{15}+...) (x0+x5+x10+x15+...)
第三个盒子的方案: ( x 0 + x 1 + x 2 + x 3 + x 4 ) (x^0+x^1+x^2+x^3+x^4) (x0+x1+x2+x3+x4)
第四个盒子的方案: ( x 0 + x 3 ) (x^0+x^3) (x0+x3)
四个盒子的方案相互独立;
最终方案: G ( x ) = ( x 0 + x 2 + x 4 + x 6 + . . . ) ∗ ( x 0 + x 5 + x 10 + x 15 + . . . ) ∗ ( x 0 + x 1 + x 2 + x 3 + x 4 ) ∗ ( x 0 + x 3 ) G(x)=(x^0+x^2+x^4+x^6+...)*(x^0+x^5+x^{10}+x^{15}+...)*(x^0+x^1+x^2+x^3+x^4)*(x^0+x^3) G(x)=(x0+x2+x4+x6+...)∗(x0+x5+x10+x15+...)∗(x0+x1+x2+x3+x4)∗(x0+x3)
指数型生成函数
数列{an}的指数型生成函数为 H ( x ) = ∑ i = 0 ∞ a i ∗ x i i ! = a 1 ∗ x 0 0 ! + a 2 ∗ x 1 1 ! + a 3 ∗ x 2 2 ! + . . . H(x)=\sum_{i=0}^\infty\frac{a_i*x^i}{i!}=\frac{a_1*x^0}{0!}+\frac{a_2*x^1}{1!}+\frac{a_3*x^2}{2!}+... H(x)=∑i=0∞i!ai∗xi=0!a1∗x0+1!a2∗x1+2!a3∗x2+...
一些公式
举个栗子
第一个栗子
小明有n个盒子,每个盒子可以容纳一块蛋糕;他有四种蛋糕,每种蛋糕有无限个。他要选择n块蛋糕装进盒子里。其中第一种蛋糕和第二种蛋糕必须打包偶数个。求不同的打包方案。(如果两种打包方案是不同的,那么必须存在至少一个盒子在两次打包中装有不同种类的蛋糕。)
设指数型生成函数H(x),指数表示盒子数,系数表示方案数。
第一种蛋糕的方案: ( x 0 0 ! + x 2 2 ! + x 4 4 ! + . . . ) (\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...) (0!x0+2!x2+4!x4+...)
第二种蛋糕的方案: ( x 0 0 ! + x 2 2 ! + x 4 4 ! + . . . ) (\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...) (0!x0+2!x2+4!x4+...)
第三种蛋糕的方案: ( x 0 0 ! + x 1 1 ! + x 2 2 ! + . . . ) (\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...) (0!x0+1!x1+2!x2+...)
第四种蛋糕的方案: ( x 0 0 ! + x 1 1 ! + x 2 2 ! + . . . ) (\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...) (0!x0+1!x1+2!x2+...)
四种蛋糕的方案相互独立;
最终方案:
H ( x ) = ( x 0 0 ! + x 2 2 ! + x 4 4 ! + . . . ) 2 ∗ ( x 0 0 ! + x 1 1 ! + x 2 2 ! + . . . ) 2 H(x)=(\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...)^2*(\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...)^2 H(x)=(0!x0+2!x2+4!x4+...)2∗(0!x0+1!x1+2!x2+...)2
= ( e x + e − x 2 ) 2 ∗ e 2 ∗ x =(\frac{e^x+e^{-x}}{2})^2*e^{2*x} =(2ex+e−x)2∗e2∗x
= e 4 ∗ x + 2 ∗ e 2 ∗ x + 1 4 =\frac{e^{4*x}+2*e^{2*x}+1}{4} =4e4∗x+2∗e2∗x+1
= 1 4 + ∑ i = 0 ∞ 4 n + 2 n + 1 4 ∗ x n n ! =\frac14+\sum_{i=0}^{\infty}\frac{4^n+2^{n+1}}4*\frac{x^n}{n!} =41+∑i=0∞44n+2n+1∗n!xn
与普通生成函数相似,给n个盒子装入蛋糕的方案数为函数H(x)指数为n的项的系数 4 n + 2 n + 1 4 \frac{4^n+2^{n+1}}4 44n+2n+1
第二个栗子
被我吃掉了。
生成函数的运算
- F+G意义为可能是两种情况中的一种
- FG意义为同时选择两种情况
- EF意义为自我组合
其他
待续……