春季个人训练赛-3、4
1、 Parentheses
A bracket is a punctuation mark, which is used in matched pairs, usually used within articles or
programs. Brackets include round brackets, square brackets, curly brackets, angle brackets, and various
other pairs of symbols. Let’s focus on the round brackets, also called parentheses.
A sequence of parentheses is said to be well-formed if the parentheses are properly nested.
For example, A = a1a2 . . . a18 = “(()())()()()(())()” is well-formed, but B = b1b2 . . . b18 =
“(()())))(((((())((” is not. (See Figure 1.) More formally, a sequence of parentheses P = p1p2 . . . pn
is well-formed if

Figure 1. Two sequences of parentheses.
AutoText is a company, which is developing a text editor for programmers. The new editor will
provide many powerful functions to automatically correct typing errors. On a keyboard, the left and
right parentheses are adjacent. Thus, it is often that “)” is mistyped as “(” or vice versa. And therefore,
one of the functions AutoText wants to provide is to automatically convert a sequence of parentheses
P (that may not be well-formed) into a wellformed sequence P
′
. In the conversion, the only allowed
operation is to reverse a parenthesis (i.e., either to replace a “(” with a “)” or to replace a “)” with
a “(”). For example, in Figure 1, we can convert B into the well-formed sequence A by performing 4
reverse operations on b7, b10, b12, b18 . Of course, there may be several ways to convert a sequence into
a well-formed sequence. A conversion is optimal if it uses the minimum number of reverse operations.
Please write a program to compute the minimum number of reverse operations that make a given
sequence of parentheses P = p1p2 . . . pn well-formed.
Input
The first line contains an integer T ≤ 10 indicating the number of test cases. The first line of each test
case contains an even integer n, 2 ≤ n ≤ 100, indicating the length of P. Next, the second line gives
the sequence P.
Output
For each test case, output the minimum number of reverse operations that make P well-formed.
Sample Input
3
18
(()())))(((((())((
2
()
8
(()))()(
Sample Output
4
0
2
题意:
给定字符串,然后去判断左右括号是不是合法的
合法:() 、(())、()()()
不合法:))、((、)(
把不合法的转化成合法的,求需要的最少补数?
思路:
首先把合法的字符从该字符串中去掉,留下的是不合法的,然后讨论一下情况:
交换的最少步数,如果相邻的可以通过转化就可以变成合法的,那么步数肯定最少
1、如果是 )) 或者 (( ,则转化一次就可以变成 ()
2、如果是 )(,则需要转化两次
CODE:
#include
#include
#include
#include
#include
#include 2、 Least Crucial Node
A wireless sensor network is a self-organizing network without specific infrastructure. It is a multi-hop
network in which sensor nodes can be randomly deployed and the data transmission between nodes
usually involves other intermediate nodes. Sensor nodes are often deployed in outdoor or hazardous
environments. Power outage of sensors can lead to node failure and cause many serious problem. For
example, node failure can disconnect the whole network, causing data from one part of the network to
fail to transmit to another part of the network. It is difficult to replace failed sensor nodes in hazardous
conditions or far-reaching areas such as rainforests or high mountains.
Wireless sensor networks usually connect to the outside world through the so called sinks (may be
regarded as gateways). All data collected by sensor nodes are sent to the sink, and then the sink relays
such data to remote users or servers through the Internet, satellite, or any viable medium.
A wireless sensor network can be modeled by a graph with each vertex (edge) representing a sensor
(a two-way communication link). In the following figure, nodes 4, 10, and 14 are more crucial to the
connectivity of the network since a power shortage in any one of them can lead to a disconnected
network.
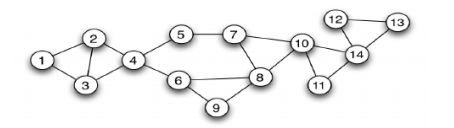
Suppose that node 1 is the sink node. The failure of node 4 disconnects nodes in the set
{5, 6, 7, 8, 9, 10, 11, 12, 13, 14} from the sink. The failure of node 10 disconnects the nodes in the set
{11, 12, 13, 14} from the sink. Lastly, the failure of node 14 disconnects the nodes in {12, 13} from the
sink. This means node 4 is more crucial than nodes 10 and 14 in network connectivity; thus we call
node 4 a crucial node of the network. Notice that crucial nodes do not include the sink. Specifically,
the failure of a crucial node in a given sensor network disconnects the largest number of nodes from
the sink. Moreover, the least crucial node is a crucial node with the least number label among all the
crucial nodes.
Please write a program to find the least crucial node for a given sensor network with a specific sink.
Input
There are several input lines to a test case. The first line of each test case contains an integer n
(2 ≤ n ≤ 100), where n is the number of nodes (vertex set of G) labeled with {1, 2, . . . , n} in the
network. The second line contains an integer, which is the label of the unique sink of the network. The
third line contains an integer m, indicating the number of communication links in the network. The
next m lines each contains a pair of integers, say i and j (separated by a space), denoting there is a
communication link (edge in E) between node i and node j. There are at most 10 test cases and n = 0
denotes end of the test cases.
Output
The output for each instance should contain an integer denoting the least crucial node in the given
network.
Sample Input
4
4
3
1 2
2 3
3 4
6
3
8
1 2
2 3
2 4
2 5
3 4
3 5
4 5
5 6
0
Sample Output
3
2
题意:
图
n个点,m条边,当顶点k从图中割掉时,哪个点带走的点最多(也就是说,当这个点从图中割点时,会使与之相连的点断开,然后和原本图分开)
思路:
去找与k相连的点 度 最大的那个点,就是受影响最大的点
#include
#include
#include
#include
#include
#include Sample Input
31
24 3
3 15
0
Sample Output
7
21
题意:
定义了一种新的乘法:
AB = ( A * B ) % P
利用同余定理
A B = ( ( A % P ) * ( B % P ) ) % P
![]()
已知a和b的值,求X的值是多少?
注意
a*a =( ( a % p ) * ( a % p ) ) % p
思路:暴力好啦
用到了同余定理
但是需要注意的是,用 long long 和 调用会超时
如果a和b相等的话,x的值就是1
#include
#include
#include
#include
#include
#include 4、 Von Neumann’s Fly
The following problem was posed to John von Neumann:
Two bicyclists, A and B, start riding toward each other at the same time from places that
are 250 miles apart, A traveling at 10 miles per hour, and B at 15 miles per hour. At the
same time, a fly leaves the front wheel of A’s bicycle, and flies toward B’s bicycle at 20
miles per hour. As soon as he touches the front wheel of B’s bicycle, he turns around and
flies back. As the bicycles approach each other, he continues flying back and forth, touching
each front wheel in turn, until, alas, he is crushed between them. Since the fly travels faster
than either cyclist, he makes an infinite number of trips, yet travels a finite distance (the
infinite series converges). How far did the fly travel?
Von Neumann immediately summed the infinite series (in his head!), and arrived at the correct
answer: 200 miles.
You are to write a program that solves a more general version of that problem, with varying initial
distances and speeds.
Input
The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets
that follow. Each data set should be processed identically and independently.
Each data set consists of a single line containing five values: an integer N (the data set number),
and four floating-point values: D (the initial distance between the bicycles, 10 ≤ D ≤ 1000), A (cyclist
A’s speed in miles per hour, 1 ≤ A ≤ 30), B (cyclist B’s speed in miles per hour, 1 ≤ B ≤ 30), and F
(the fly’s speed in miles per hour, A ≤ B < F ≤ 50).
Output
For each data set there is one line of output. It contains the data set number followed by a single space,
followed by the number of miles traveled by the fly, (the sum of the infinite series described by the
input values), accurate to two decimal places.
Sample Input
5
1 250 10 15 20
2 10.7 3.5 4.7 5.5
3 523.7 15.3 20.7 33.3
4 1000 30 30 50
5 500 15 15 25
Sample Output
1 200.00
2 7.18
3 484.42
4 833.33
5 416.67
题意:
给定 AB距离总路程、A的速度、B的速度、飞机的速度
AB各从甲乙地出发,飞机从甲地出发,当遇到A或者B的时候,需要回头
问当AB相遇时飞机走过的路程?
思路:
求出AB相遇的时间,再乘飞机的速度,就知道飞机的路程
CODE:
#include
#include
#include
#include
#include
#include 5、
6468 Pisano Periods
In 1960, Donald Wall of IBM, in White Plains, NY, proved that the series obtained by taking each
element of the Fibonacci series modulo m was periodic.
For example, the first ten elements of the Fibonacci sequence, as well as their remainders modulo
11, are:

For this problem, you must write a program that calculates the length of the repeating subsequence,
k(m), for different modulo values m.
Input
The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets
that follow. Each data set is a single line that consists of two space separated integer values N and M.
N is the data set number. M is the modulo value (2 ≤ M ≤ 1, 000, 000).
Output
For each data set there is one line of output. It contains the data set number (N) followed by a single
space, followed by the length of the repeating subsequence for M, k(M).
Sample Input
5
1 4
2 5
3 11
4 123456
5 987654
ACM-ICPC Live Archive: 6468 – Pisano Periods 2/2
Sample Output
1 6
2 20
3 10
4 15456
5 332808
题意:
知道斐波那契数列,给定 mod ,对斐波那契数列进行求余,问循环周期是多少?
例如图片上:
对 11 求余时,循环周期是 10
思路:
一开始按照图片上给定的规律来写,后来 WA,感觉图片是误人的 hhh
然后就想到如果是能够循环的话,只要出现了最后一位的0和第一位的1,就能够在开始一新的一轮循环
所以想到只要找到前后两个是1和0的,就可以确定一个循环周期
CODE:
#include
#include
#include
#include
#include
#include 