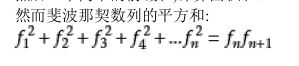春季个人训练赛 5(广工新生赛)
1、A - hzy 和zsl 的生存挑战
Description
zsl 和hzy 来到了臭臭城堡,打算挑战臭臭城堡的大魔王hyz,大魔王hyz设置了这样的一个挑战:
1. zsl 和hzy两个人各自来到一间密室,期间两人无法以任何形式交流
2. 大魔王hyz会随机在两个人的脑海里各发送一个数字,0或者是1
3. zsl 和 hzy 需要猜对这俩个数字才算通关,但是大魔王hyz觉得人生不能过于无敌,因此降低难度,只要两个人中有一个人答对就算是通关
现在大魔王hyz 给出的数字可能的情况有 00, 01, 10, 11 四种,请按上述枚举的顺序,计算所有情况下zsl 和hzy 通关的几率。(假设zsl 和 hzy 两个人都足够机智,能够选择出最优决策)
Input
(空)
Output
输出四个答案,每个答案后面跟随一个换行符并且保留两位小数位,分别对应00,01,10,11的情况下,zsl和hzy通关的几率
Sample Input
(空)
Sample Output
1.00
0.00
0.50
0.55 (输出仅做格式参考,不保证正确性)思路:
CODE:
#include
#include
#include
#include
#include
#include
#include
2、
作为CNCS的半壁江山,狗哥常常在宇宙中心邵阳眺望黄浦江,夜晚的星空总是迷人,有时候还能见到彗星滑落。
狗哥是幸运的,他在两秒钟内看到了十七颗彗星划过天际,作为打ACM的学者,自然不会有「稳定-1」情况。他开始研究彗星运动的轨迹,发现他们都遵照斐波那契螺旋线在运动着。
尤里卡!狗哥觉得这就是找寻「生命,宇宙和一切的终极答案」的精要所在,但是怎么表示呢?狗哥觉得求取斐波那契螺旋线经过的一个个方格的面积之和就是公式的表现。
例如下图,螺旋线每划过一个方格,都转过了四分之一圈。如果我们以四分之一圈为单位,那么我们用类似带分数的形式表示螺旋线转动的起点和终点。例如,0+0 到 0 + 1 意即从第一个方格转到第二个方格,划过了前两个方格,他们的面积之和为2(1+1)。同理,0+0 到 1+0 划过了前五个方格,他们的面积之和为40(1+1+4+9+25)。
但是聪明的狗哥需要一个程序去获得指定范围内的螺旋线面积之和,狗哥给了你一首「希望之花」的时间,而他需要利用这个时间去打出四暗刻单骑。如果你能完成这个程序,狗哥会封你为格拉摩根伯爵
Input
不定组数据。
首先输入一个整数Q,代表狗哥询问次数。
接下来Q行,每行四个整数a,b,c,d,代表狗哥想求 a+b 到 c+d 之间的螺旋线面积之和。
1<= Q <= 10000
0<= a,c <= 10000
0 <= b,d <= 3
结果对192600817取模。
Output
一个数字,表示螺旋线面积之和。
Sample Input
4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3
4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3
Sample Output
2
40
47
91
98
2
40
47
91
98
题意:
题目上说的 0+0 到 0+1 走了两个方格,可以理解成 [0,0] 和 [0,1]
0+0 到 1+0 走了五个方格,可以理解成 [0,0],[0,1],[0,2],[0,3],[1,0]
所以我们把他的坐标理解成二维数组中的下标 (0<=i<=1000, 0<=j<=3 最多1001行,4列的二维数组)
面积:
斐波那契的平方形式:
1 1 4 9
25 64 169 441
...
思路:
我们把坐标变成求数组中的第几个位置
假设 (i,j) pos = 4*i + j + 1
已知两个点的位置,然后根据 前缀和 的思想直接求出面积 s[ pos ] - s[ pos1 ]
需要注意:
①:如果两个点的位置相等,代表的是该小正方形的面积,就是 s[pos]
②:如果第一个点的位置大于第二个点的位置,记得交换
③:需要求余,利用同余定理,
如果出现了负数,需要再加上 mod
CODE:
#include
#include
#include
#include
#include
#include
#include
3、C - 超级无敌简单题
Description
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
鸽子数字由以下过程定义:从任何正整数开始,将数字替换为其各个数位的平方和,并重复该过程,直到该数字等于1。如果不能,则这个数字不是鸽子数。
例如7是鸽子数,因为7->49->97->130->10->1。(7*7=49,4*4+9*9=97,9*9+7*7=130....如此类推)
显然1是第一个鸽子数。
有Q个询问,每个询问给出一个数k,你需要输出第k个鸽子数。
Input
第一行一个Q,代表询问的个数(Q<=100000)
接下来Q行,每行一个数字k(k<150000)
Output
每行输出一个数,代表第k个鸽子数
Sample Input
2
1
2
Sample Output
1
7
题意:
鸽子树的定义(和 happy prim 类似)
思路:
需要查询 150000 个鸽子数,全部打表肯定T
所以可以先对前 1000 个数进行打表,将鸽子数存起来
1000 之后的数字只要其平方存在这些鸽子数中,这个肯定是鸽子数,否则不是
由于需要查询 150000个鸽子数,所以需要循环到 1000000 (这个也不好掌握,WA了几次也没想起来这个范围)
CODE :
#include
#include
#include
#include
#include
#include
#include
4、
Input
多组输入,每组输入占一行,包含一个整数n(1 <= n <= 1e18)。
数据不超过300000组。
Output
对于每组输入,输出一行,包括一个数代表答案。
Sample Input
5
100
Sample Output
129
660756544
推公式,用到了 组合数学公式和错位相减法
得到公式:
F(n) = ( n - 1) * 2^n + 1
不能用 pow(n,2) % mod ( pow 是 double 型的),要用快速幂求 2^n
用到同余定理
#include
#include
#include
#include
#include
#include
#include