算法入门6:回溯法
一. 回溯法 – 深度优先搜素
1. 简单概述
回溯法思路的简单描述是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
基本思想类同于:
- 图的深度优先搜索
- 二叉树的后序遍历
【
分支限界法:广度优先搜索
思想类同于:图的广度优先遍历
二叉树的层序遍历
】
2. 详细描述
详细的描述则为:
回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树,当算法搜索至解空间树的某一节点时,先利用剪枝函数判断该节点是否可行(即能得到问题的解)。如果不可行,则跳过对该节点为根的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先策略搜索。
回溯法的基本行为是搜索,搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类:1. 使用约束函数,剪去不满足约束条件的路径;2.使用限界函数,剪去不能得到最优解的路径。
问题的关键在于如何定义问题的解空间,转化成树(即解空间树)。解空间树分为两种:子集树和排列树。两种在算法结构和思路上大体相同。
3. 回溯法应用
当问题是要求满足某种性质(约束条件)的所有解或最优解时,往往使用回溯法。
它有“通用解题法”之美誉。
二. 回溯法实现 - 递归和递推(迭代)
回溯法的实现方法有两种:递归和递推(也称迭代)。一般来说,一个问题两种方法都可以实现,只是在算法效率和设计复杂度上有区别。【类比于图深度遍历的递归实现和非递归(递推)实现】
1. 递归
思路简单,设计容易,但效率低,其设计范式如下:
//针对N叉树的递归回溯方法
void backtrack (int t)
{
if (t>n) output(x); //叶子节点,输出结果,x是可行解
else
for i = 1 to k//当前节点的所有子节点
{
x[t]=value(i); //每个子节点的值赋值给x
//满足约束条件和限界条件
if (constraint(t)&&bound(t))
backtrack(t+1); //递归下一层
}
}
2. 递推
算法设计相对复杂,但效率高。
//针对N叉树的迭代回溯方法
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if(ExistSubNode(t)) //当前节点的存在子节点
{
for i = 1 to k //遍历当前节点的所有子节点
{
x[t]=value(i);//每个子节点的值赋值给x
if (constraint(t)&&bound(t))//满足约束条件和限界条件
{
//solution表示在节点t处得到了一个解
if (solution(t)) output(x);//得到问题的一个可行解,输出
else t++;//没有得到解,继续向下搜索
}
}
}
else //不存在子节点,返回上一层
{
t--;
}
}
}三. 子集树和排列树
1. 子集树
所给的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间成为子集树。如0-1背包问题,从所给重量、价值不同的物品中挑选几个物品放入背包,使得在满足背包不超重的情况下,背包内物品价值最大。它的解空间就是一个典型的子集树。
回溯法搜索子集树的算法范式如下:
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (constraint(t)&&bound(t)) backtrack(t+1);
}
}
2. 排列树
所给的问题是确定n个元素满足某种性质的排列时,相应的解空间就是排列树。如旅行售货员问题,一个售货员把几个城市旅行一遍,要求走的路程最小。它的解就是几个城市的排列,解空间就是排列树。
回溯法搜索排列树的算法范式如下:
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (constraint(t)&&bound(t)) backtrack(t+1);
swap(x[t], x[i]);
}
}
四. 经典问题
(1)装载问题(2)0-1背包问题
(3)旅行售货员问题
(4)八皇后问题
(5)迷宫问题
(6)图的m着色问题
1. 0-1背包问题
问题:给定n种物品和一背包。物品i的重量是wi,其价值为pi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?分析:问题是n个物品中选择部分物品,可知,问题的解空间是子集树。比如物品数目n=3时,其解空间树如下图,边为1代表选择该物品,边为0代表不选择该物品。使用x[i]表示物品i是否放入背包,x[i]=0表示不放,x[i]=1表示放入。回溯搜索过程,如果来到了叶子节点,表示一条搜索路径结束,如果该路径上存在更优的解,则保存下来。如果不是叶子节点,是中点的节点(如B),就遍历其子节点(D和E),如果子节点满足剪枝条件,就继续回溯搜索子节点。
代码:
#include
#define N 3 //物品的数量
#define C 16 //背包的容量
int w[N]={10,8,5}; //每个物品的重量
int v[N]={5,4,1}; //每个物品的价值
int x[N]={0,0,0}; //x[i]=1代表物品i放入背包,0代表不放入
int CurWeight = 0; //当前放入背包的物品总重量
int CurValue = 0; //当前放入背包的物品总价值
int BestValue = 0; //最优值;当前的最大价值,初始化为0
int BestX[N]; //最优解;BestX[i]=1代表物品i放入背包,0代表不放入
//t = 0 to N-1
void backtrack(int t)
{
//叶子节点,输出结果
if(t>N-1)
{
//如果找到了一个更优的解
if(CurValue>BestValue)
{
//保存更优的值和解
BestValue = CurValue;
for(int i=0;i //约束条件:放的下
if((CurWeight+w[t])<=C)
{
CurWeight += w[t];
CurValue += v[t];
backtrack(t+1);
CurWeight -= w[t];
CurValue -= v[t];
}
}
}
//PS:上述代码为了更符合递归回溯的范式,并不够简洁
}
}
int main(int argc, char* argv[])
{
backtrack(0);
printf("最优值:%d\n",BestValue);
for(int i=0;i 2. 旅行售货员问题
回溯法----旅行售货员问题
3. 详细描述N皇后问题
问题:在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
N皇后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
分析:从n×n个格子中选择n个格子摆放皇后。可见解空间树为子集树。
使用Board[N][N]来表示棋盘,Board[i][j]=0 表示(I,j)位置为空,Board[i][j]=1 表示(I,j)位置摆放有一个皇后。
全局变量way表示总共的摆放方法数目。
使用Queen(t)来摆放第t个皇后。Queen(t) 函数符合子集树时的递归回溯范式。当t>N时,说明所有皇后都已经摆 放完成,这是一个可行的摆放方法,输出结果;否则,遍历棋盘,找皇后t所有可行的摆放位置,Feasible(i,j) 判断皇后t能否摆放在位置(i,j)处,如果可以摆放则继续递归摆放皇后t+1,如果不能摆放,则判断下一个位置。
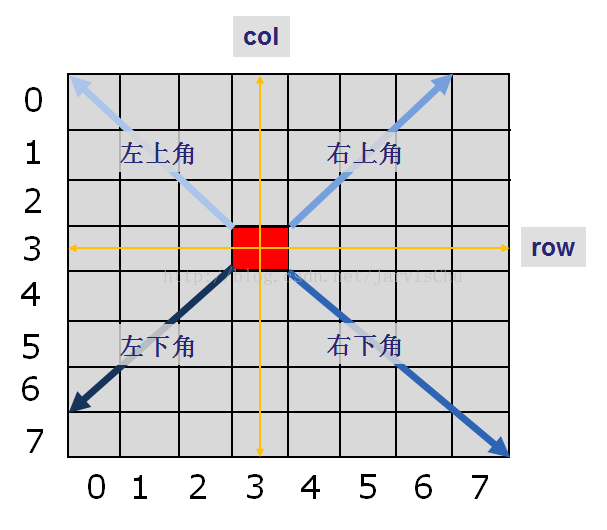
Feasible(row,col)函数首先判断位置(row,col)是否合法,继而判断(row,col)处是否已有皇后,有则冲突,返回0,无则继续判断行、列、斜方向是否冲突。斜方向分为左上角、左下角、右上角、右下角四个方向,每次从(row,col)向四个方向延伸一个格子,判断是否冲突。如果所有方向都没有冲突,则返回1,表示此位置可以摆放一个皇后。
代码:
/************************************************************************
* 名 称:NQueen.cpp
* 功 能:回溯算法实例:N皇后问题
* 作 者:JarvisChu
* 时 间:2013-11-13
************************************************************************/
#include
#define N 8
int Board[N][N]; //棋盘 0表示空白 1表示有皇后
int way; //摆放的方法数
//判断能否在(x,y)的位置摆放一个皇后;0不可以,1可以
int Feasible(int row,int col)
{
//位置不合法
if(row>N || row<0 || col >N || col<0)
return 0;
//该位置已经有皇后了,不能
if(Board[row][col] != 0)
{ //在行列冲突判断中也包含了该判断,单独提出来为了提高效率
return 0;
}
//////////////////////////////////////////////////
//下面判断是否和已有的冲突
//行和列是否冲突
for(int i=0;i=0 && (col-i)>=0) //位置合法
{
if(Board[row-i][col-i] != 0)//此处已有皇后,冲突
return 0;
}
//左下角
if((row+i)=0)
{
if(Board[row+i][col-i] != 0)
return 0;
}
//右上角
if((row-i)>=0 && (col+i)N)
{
way++;
/*如果N较大,输出结果会很慢;N较小时,可以用下面代码输出结果
for(int i=0;i PS:该问题还有更优的解法。充分利用问题隐藏的约束条件:每个皇后必然在不同的行(列),每个行(列)必然也只有一个皇后。这样我们就可以把N个皇后放到N个行中,使用Pos[i]表示皇后i在i行中的位置(也就是列号)(i = 0 to N-1)。这样代码会大大的简洁,因为节点的子节点数目会减少,判断冲突也更简单。
4. 迷宫问题
问题:给定一个迷宫,找到从入口到出口的所有可行路径,并给出其中最短的路径
分析:用二维数组来表示迷宫,则走迷宫问题用回溯法解决的的思想类似于图的深度遍历。从入口开始,选择下一个可以走的位置,如果位置可走,则继续往前,如果位置不可走,则返回上一个位置,重新选择另一个位置作为下一步位置。
N表示迷宫的大小,使用Maze[N][N]表示迷宫,值为0表示通道(可走),值为1表示不可走(墙或者已走过);
Point结构体用来记录路径中每一步的坐标(x,y)
(ENTER_X,ENTER_Y) 是迷宫入口的坐标
(EXIT_X, EXIT _Y) 是迷宫出口的坐标
Path容器用来存放一条从入口到出口的通路路径
BestPath用来存放所有路径中最短的那条路径
Maze()函数用来递归走迷宫,具体步骤为:
1. 首先将当前点加入路径,并设置为已走
2. 判断当前点是否为出口,是则输出路径,保存结果;跳转到4
3. 依次判断当前点的上、下、左、右四个点是否可走,如果可走则递归走该点
4. 当前点推出路径,设置为可走
代码:
/************************************************************************
* 名 称:Maze.cpp
* 功 能:回溯算法实例:迷宫问题
* 作 者:JarvisChu
* 时 间:2013-11-13
************************************************************************/
#include
#include
using namespace std;
typedef struct
{
int x;
int y;
}Point;
#define N 10 //迷宫的大小
#define ENTER_X 0 //入口的位置(0,0)
#define ENTER_Y 0
#define EXIT_X N-1 //出口的位置(N-1,N-1)
#define EXIT_Y N-1
int Maze[N][N]; //定义一个迷宫,0表示通道,1表示不可走(墙或已走)
int paths; //路径条数
vector Path; //保存一条可通的路径
vector BestPath; //保存最短的路径
bool First = true; //标志,找到第一条路径
//初始化迷宫
void InitMaze()
{
//简单起见,本题定义一个固定大小10*10的迷宫
//定义一个迷宫,0表示通道,1表示墙(或不可走)
int mz[10][10]={
{0,0,1,1,1,1,1,1,1,1}, //0
{1,0,0,1,1,0,0,1,0,1}, //1
{1,0,0,1,0,0,0,1,0,1}, //2
{1,0,0,0,0,1,1,0,0,1}, //3
{1,0,1,1,1,0,0,0,0,1}, //4
{1,0,0,0,1,0,0,0,0,1}, //5
{1,0,1,0,0,0,1,0,0,1}, //6
{1,0,1,1,1,0,1,1,0,1}, //7
{1,1,0,0,0,0,0,0,0,0}, //8
{1,1,1,1,1,1,1,1,1,0} //9
// 0 1 2 3 4 5 6 7 8 9
};
//复制到迷宫
memcpy(Maze,mz,sizeof(mz));
paths = 0;
}
//从(x,y)位置开始走;初始为(0,0)
void MazeTrack(int x,int y)
{
///////////////////////////////////////
//当前点加入到路径
Point p={x,y};
Path.push_back(p);
Maze[x][y] = 1; //设置为已走,不可走
//cout<<"来到("<::iterator it;
for(it=Path.begin();it!=Path.end();++it)
{
cout<<"("<x<<","<y<<") ";
}
cout<=0 && Maze[x-1][y]==0)//上(x-1,y);存在且可走
{
MazeTrack(x-1,y);
}
if((x+1)=0 && Maze[x][y-1]==0)//左(x,y-1);存在且可走
{
MazeTrack(x,y-1);
}
if((y+1)::iterator it;
for(it=BestPath.begin();it!=BestPath.end();++it)
{
cout<<"("<x<<","<y<<") ";
}
cout< PS:用WPF实现了一个简单的图形化迷宫程序。白色表示通道,红色表示墙,最短的路径用黄色显示。目前实现了一个10*10的迷宫自动搜素最短通路,右侧显示搜索过程中得到的每一个可行通路。
由于构造一个迷宫比较复杂,所以暂时“迷宫设置”功能没有做实现,至于手动一步步查看搜素过程的动画也没有做实现。
实现的大致思路如下:迷宫的数据使用二维数据mazeData表示。迷宫的显示使用Grid控件表示,每个方格处添加一个Rectangle控件,如果该方格mazeData值为0,则填充白色值为1,则填充红色,值为2则填充黄色。
XAML代码为:
对应的MainWindow.xaml.cs代码为:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Data;
using System.Windows.Documents;
using System.Windows.Input;
using System.Windows.Media;
using System.Windows.Media.Imaging;
using System.Windows.Navigation;
using System.Windows.Shapes;
namespace MazeAnimation
{
///
/// Interaction logic for MainWindow.xaml
///
public partial class MainWindow : Window
{
public struct Point
{
public int x;
public int y;
public Point(int a, int b) { x = a; y = b; }
};
public bool bAutoRun = true;
public int mazeHeight = 10;
public int mazeWidth = 10;
int[,] mazeData = new int[10, 10]
{
{0,0,1,1,1,1,1,1,1,1}, //0
{1,0,0,1,1,0,0,1,0,1}, //1
{1,0,0,1,0,0,0,1,0,1}, //2
{1,0,0,0,0,1,1,0,0,1}, //3
{1,0,1,1,1,0,0,0,0,1}, //4
{1,0,0,0,1,0,0,0,0,1}, //5
{1,0,1,0,0,0,1,0,0,1}, //6
{1,0,1,1,1,0,1,1,0,1}, //7
{1,1,0,0,0,0,0,0,0,0}, //8
{1,1,1,1,1,1,1,1,1,0} //9
// 0 1 2 3 4 5 6 7 8 9
};
public int enterX = 0;
public int enterY = 0;
public int exitX = 9;
public int exitY = 9;
public int runSpeed = 100;
public int paths = 0; //总条数
public Stack path = new Stack(); //一条找到的路径
public Stack bestPath = new Stack();//最优路径
public bool bFrist = true;
public MainWindow()
{
InitializeComponent();
}
//显示迷宫,白色0表示通道,红色1表示不可走,黄色2表示最优的路径,绿色3表示已经走过的路径
private void DisplayMaze()
{
gdMaze.Children.Clear();
//设置可走和不可走
for (int i = 0; i < mazeHeight; i++)
{
for (int j = 0; j < mazeWidth; j++)
{
Rectangle rect = new Rectangle();
rect.SetValue(Grid.RowProperty, i);
rect.SetValue(Grid.ColumnProperty, j);
if (mazeData[i, j] == 0)
{
rect.Fill = Brushes.White;
}
else if (mazeData[i, j] == 1)
{
rect.Fill = Brushes.Red;
}
else if (mazeData[i, j] == 2)
{
rect.Fill = Brushes.Yellow;
}
else if (mazeData[i, j] == 3)
{
rect.Fill = Brushes.Blue;
}
gdMaze.Children.Add(rect);
}
}
}
//初始化迷宫
private void InitMaze()
{
gdMaze.Background = Brushes.LightGray;
gdMaze.ShowGridLines = true;
for (int i = 0; i < mazeHeight; i++)
{
gdMaze.RowDefinitions.Add(new RowDefinition());
}
for (int i = 0; i < mazeWidth; i++)
{
gdMaze.ColumnDefinitions.Add(new ColumnDefinition());
}
DisplayMaze();
}
//从(x,y)位置开始走;初始为(0,0)
private void MazeTrack(int x, int y)
{
///////////////////////////////////////
//当前点加入到路径
Point p = new Point(x, y);
path.Push(p);
mazeData[x, y] = 3; //设置为已走,不可走
//DisplayMaze();
//System.Threading.Thread.Sleep(runSpeed);//休眠
///////////////////////////////////////
//如果该位置是出口,输出结果
if (x == exitX && y == exitY)
{
string msg = "找到一条道路(逆序)\n";
tbLog.AppendText(msg);
paths++;
//输出路径
foreach (Point pnt in path)
{
msg = "(" + pnt.x + "," + pnt.y + ")";
tbLog.AppendText(msg);
}
tbLog.AppendText("\n\n");
//判断是否更优
if (bFrist)//如果是找到的第一条路径,直接复制到最优路径
{
foreach (Point pnt in path)
{
bestPath.Push(pnt);
}
bFrist = false;
}
else //不是第一条,则判断是否更短
{
//更短,复制到最优路径
if (path.Count < bestPath.Count)
{
bestPath.Clear();
foreach (Point pnt in path)
{
bestPath.Push(pnt);
}
}
}
}
///////////////////////////////////////
//判断(x,y)位置的上、下、左、右是否可走
if ((x - 1) >= 0 && mazeData[x - 1, y] == 0)//上(x-1,y);存在且可走
{
MazeTrack(x - 1, y);
}
if ((x + 1) < mazeHeight && mazeData[x + 1, y] == 0)//下(x+1,y);存在且可走
{
MazeTrack(x + 1, y);
}
if ((y - 1) >= 0 && mazeData[x, y - 1] == 0)//左(x,y-1);存在且可走
{
MazeTrack(x, y - 1);
}
if ((y + 1) < mazeWidth && mazeData[x, y + 1] == 0)//右(x,y+1);存在且可走
{
MazeTrack(x, y + 1);
}
///////////////////////////////////////
//返回上一步
path.Pop();
mazeData[x, y] = 0; //设置为未走
//DisplayMaze();
//System.Threading.Thread.Sleep(runSpeed);//休眠
}
private void Window_Loaded(object sender, RoutedEventArgs e)
{
//初始化变量
tbMazeHeight.Text = mazeHeight.ToString();
tbMazeWidth.Text = mazeWidth.ToString();
tbEnterX.Text = enterX.ToString();
tbEnterY.Text = enterY.ToString();
tbExitX.Text = exitX.ToString();
tbExitY.Text = exitY.ToString();
cbAutoRun.IsChecked = bAutoRun;
tbAutoRunSpeed.Text = runSpeed.ToString();
//初始化迷宫
InitMaze();
}
//点击开始
private void btnStart_Click(object sender, RoutedEventArgs e)
{
string msg = "开始走迷宫\n";
tbLog.AppendText(msg);
MazeTrack(enterX, enterY);
//显示最优的路径
msg = "\n可行路径总条数为" + paths + "\n最优路径为\n";
tbLog.AppendText(msg);
foreach (Point pnt in bestPath)
{
msg = "(" + pnt.x + "," + pnt.y + ")";
tbLog.AppendText(msg);
mazeData[pnt.x, pnt.y] = 2;
}
DisplayMaze();
}
//下一步
private void btnNext_Click(object sender, RoutedEventArgs e)
{
string msg = "手动开始走迷宫 暂未实现\n";
tbLog.AppendText(msg);
}
}
}
参考文献: 《计算机算法设计与分析》(王晓东)
转载本文请注明作者和出处
作者 :JarvisChu
出处:http://blog.csdn.net/jarvischu