算法入门8:随机算法
之前将的算法都是确定的,即对于相同的输入总对应着相同的输出。但实际中也常常用到不确定的算法,比如随机数生成算法,算法的结果是不确定的,我们称这种算法为(随机)概率算法,分为如下四类:
- 数值概率算法
用于数值问题的求解,通常是近似解
- 蒙特卡洛算法Monte Carlo
能得到问题的一个解,但不一定是正确解,正确的概率依赖于算法运行的时间,算法所用的时间越多,正确的概率也越高。求问题的准确解;
- 拉斯维加斯算法 Las Vegas
不断调用随机算法求解,直到求得正确解或调用次数达到某个阈值。所以,如果能得到解,一定是正确解。
- 舍伍德算法 Sherwood
利用随机算法改造已有算法,使得算法的性能尽量与输入数据无关,即平滑算法的性能。它总能求得问题的一个解,且求得的解总是正确的。
1.随机数
1. 概述
计算机产生的随机数都是伪随机数,通过线性同余法得到。
d称为种子;m取值越大越好;m,b互质,常取b为质数;
2. 案例
- 伪随机数
在实际编程中,我们使用rand()函数来产生随机数,rand()函数返回0到一个最大值之间的一个随机数。
#include
#include
#include
//产生[0,100)的随机数
void GenerateRandomNumber()
{
for(int i=0;i<10;i++)
{
printf("%-4d",rand()%100);//产生[0,m)的随机数
}
printf("\n");
}
int main()
{
GenerateRandomNumber();
return 0;
}
运行代码,输出:41 67 34 0 69 24 78 58 62 64
如果我们重复运行代码就会发现,每次的输出结果都是这个序列。这就是因为rand产生的随机序列是伪随机序列。解决方法是:使用当前的时间作为随机种子。
- 时间作为随机种子
srand((unsigned)time(0));//以当前时间作为种子2. 数值概率算法的应用
(1)随机投点法计算π
(2)计算定积分
(3)解非线性方程组
1. 随机投点法计算π
如下图,正方形及其内切圆,圆半径为r。现向正方形中随机投n个点,所投点均匀分布,则点落入圆内概率为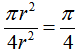 。
。
考虑第一象限即可,取r=1,投n个点,落入圆中k个点,当n趋近无穷时,k/n 趋近于![]() 。
。
#include
#include
#include
#include
float CalculatePI(int n)
{
assert(n>0);
int i=0,k=0;
float x,y;
srand((unsigned)time(NULL));
for(i=0;i 一次运行结果如下:
n=10 k=10 pi=4.000000
n=1000 k=825 pi=3.300000
n=10000000 k=8184707 pi=3.273883
2. 计算定积分
原理和计算π相同,对积分函数f(x)有约束条件:1. 在积分区域内连续;2. 在积分区域内存在最大最小值。
3. 舍伍德(Sherwood)算法
一个算法,对于不同的输入数据,其算法的性能是不一样的。比如快排算法,每次选择第一个元素作为基准,对序列从小到大排序:
平均情况:如果待排序列无序,则算法时间复杂度为O(nlogn);
最坏情况:如果序列有序(正序或逆序),则算法时间复杂度为O(n2)
舍伍德算法的思想是:设计随机算法,使得算法的性能和具体的输入值无关,算法的性能 =平均性能 + 一个很小的随机值。
舍伍德算法是为了得到好的平均性能。
准确的说:它是一种思想,并不是一个具体的实现案例。
利用随机算法可将一个算法改造成舍伍德算法,比如,快速排序时,基准的选择可以使用随机算法得到。
对于不能直接改造的,可以引入随机预处理,即对输入进行随机洗牌。比如,对于通常的排序、查找算法,可以先对待排序、查找的序列进行随机位置置换(洗牌)。
可见舍伍德算法就是一种利用随机算法改造确定性算法,使得算法的性能和输入数据尽量无关。
4.拉斯维加斯(Las Vegas)算法算法思想就是不断调用随机算法求解,直到求得正确解或者达到设定的步数。
【理解为:不断掷骰子,直到得到某个值,或掷累了】
如下面的代码:success=false;steps=0;
while(!success && (steps++)拉斯维加斯算法不一定能获得解,随着运行时间的增加,获得解的概率也越大。
它可以用来求解某些迄今没有有效解法的问题,因为通过不断的随机尝试,也许能够找到正确解。
5. 蒙特卡罗(Monte Carlo)算法拉斯维加斯算法是:不一定能给出解,给出则必正确
蒙特卡罗算法是:一定能给出解,但不一定正确
蒙特卡罗算法在一般情况下能够保证对问题的所有实例都以高概率给出正确解。但是,通常无法判断一个具体解是否正确。
一个蒙特卡罗算法得到正确解的概率为p,如果0.5 < p < 1,则称算法是正确的。p-0.5称为算法的优势。
对于用一个实例,如果蒙特卡罗算法不会给出两个不同的正确解,则称算法是一致的。
转载本文请注明作者和出处
作者 :JarvisChu
出处:http://blog.csdn.net/jarvischu

