Logistic Regression算法分析
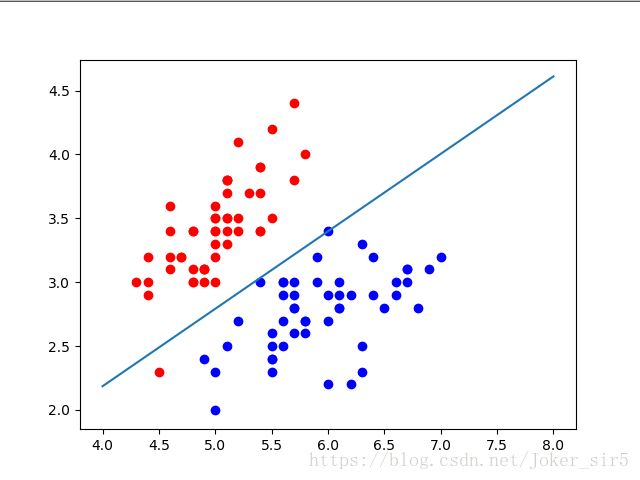
在上篇博客 中,实现了逻辑回归算法,最终也利用matplotlib画出了最终的决策面,由于数据较为简单,由经验确定的步长,迭代次数看似使得算法得到的效果良好,那如何确定此时的分类器是否达到最优呢?这将是本篇博客的工作!
超平面,截距,斜率变化趋势
由于逻辑回归处理的是二分类的问题,并且使用的iris数据集是线性可分的,所以它的决策面是一条直线,那么说到直线就有两个指标可以考量——截距,斜率,他们由最终训练出来的权重矩阵唯一确定,接下来就通过观察超平面,截距,斜率的变化趋势来判断算法是否已经收敛。
1.超平面变化趋势
在迭代过程中加入一个weightlist,用来存放每次迭代后的weight值
weightlist = []
alpha = 0.01 # 步长
maxCycles = 1000 # 设置迭代的次数
X = np.hstack([np.ones((len(data), 1)), data])
weights = np.ones(X.shape[1]) # 设置初始的参数,并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。3x1
for k in range(maxCycles):
error = error_rate(weights, X, y)
weights = weights - alpha * error # 迭代更新权重
weightlist.append(weights)可以知道,weightlist中存放有1000个3x1的weight,其中最后一个即weightlist[999]是算法最终确定的权重矩阵,由于迭代次数比较多,我们每隔200画一条决策面
X = np.linspace(4, 8, 100)
for i in range(1, len(weightlist)):
if i % 200 == 0:
weights = weightlist[i]
Y = (-weights[0] - weights[1] * X) / weights[2]
plt.plot(X, Y)
plt.annotate("i:"+str(i), xy=(X[99], Y[99]))
再把迭代次数调大些
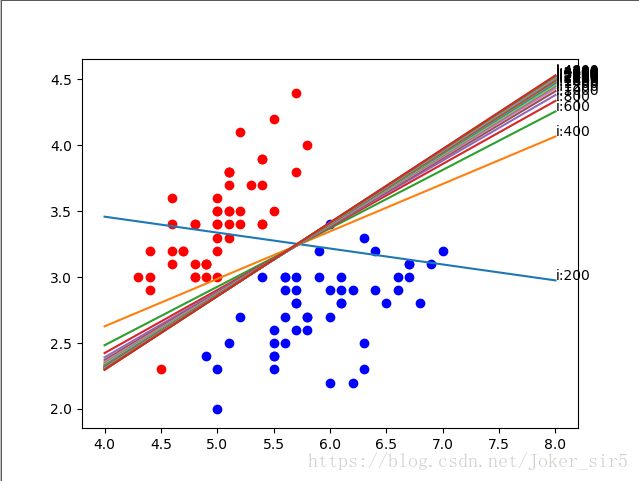
可以看到,随着迭代次数的增加,决策面变化的速度越来越小
2.截距,斜率变化趋势
我们知道决策面的方程为
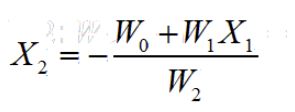
所以截距即为:-weights[0] / weights[2],斜率即为:-weights[1] / weights[2]
来看下截距和斜率的变化趋势,首先创建一个figure,并将其一分为二,(1,1)位置放截距变化趋势,(1,2)位置放斜率变化趋势,仍然利用weightlist来画图:
fig = plt.figure()
axes1 = plt.subplot(211)
axes2 = plt.subplot(212)
weightmat = np.zeros((maxCycles, X.shape[1]))
i = 0
for weight in weightlist:
weightmat[i, :] = weight.T
i += 1
x1 = np.linspace(0, maxCycles, maxCycles)
# 截距:-weights[0] / weights[2] 斜率:-weights[1] / weights[2]
axes1.plot(x1, -weightmat[:, 0] / weightmat[:, 2], c='b', linewidth=1, linestyle="-")
axes1.set_ylabel('intercept')
axes2.plot(x1, -weightmat[:, 1] / weightmat[:, 2], c='r', linewidth=1, linestyle="-")
axes2.set_ylabel('slope')
可以看到,在1000次迭代后斜率和截距变化趋于稳定,但好像还有变化趋势,将迭代次数调整到1w次,看下变化趋势:
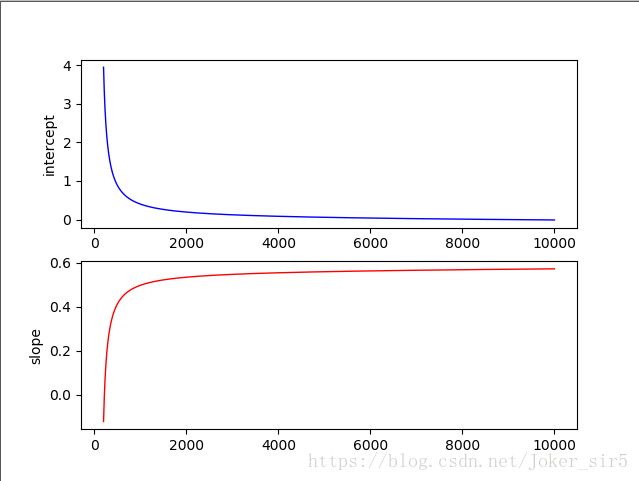
从图从可以看到基本到了2000次迭代之后截距和斜率基本不再变化,从1中决策面变化趋势也可以看得出来效果。
由于iris数据集较为简单,所以迭代到1000次的时候就会有准确率为1的效果,在实际应用中,数据可能更为复杂,结果也可能也并非由如此理想,我们可以通过察截距和斜率的变化趋势,进一步判断分类器模型是否需要进一步调整迭代次数,来使得决策面得到最优。
3.权重向量收敛评估
来分别看下各权重分量weight[0],weight[1],weight[2]的变化趋势,来看是否收敛:
x1 = np.linspace(0, maxCycles, maxCycles)
axes1.plot(x1, weightmat[:, 0], c='b', linewidth=1, linestyle="-")
axes1.set_ylabel('weight[0]')
axes2.plot(x1, weightmat[:, 1], c='r', linewidth=1, linestyle="-")
axes2.set_ylabel('weight[1]')
axes3.plot(x1, weightmat[:, 2], c='g', linewidth=1, linestyle="-")
axes3.set_ylabel('weight[2]')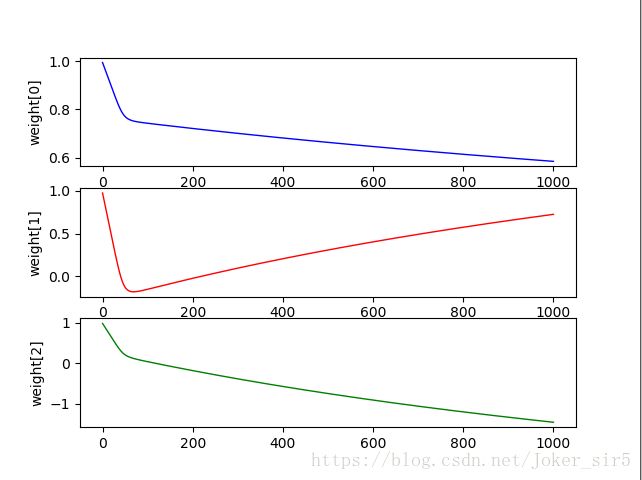
可以看到,weight[0]变化趋势呈下降状态,并无趋于平缓的趋势,weight[1]变化趋势呈上升状态,并无趋于平缓的趋势,weight[2]变化趋势呈下降状态,并无趋于平缓的趋势。
在实际问题中我们就可以通过增加迭代次数来进行进行性能调优(这里iris数据简单,但调优的思路是这样的)
随机梯度下降法
上面的调优分析主要是针对迭代次数来进行调参的,别忘了逻辑回归还有一个参数:步长,步长选择越大,收敛就越快,相应的迭代次数就越少,但迭代过程中很容越过函数最优点,出现震荡现象,在最优点附近徘徊,选择越小,收敛速度就会变慢,迭代次数也随之增加。该如何选择合适的步长,这是个问题!
所以就出现了一种平衡两者的步长策略——随机梯度下降法,既保证优化精度,又提升收敛速度。
思路:随机抽取样本,针对每个向量动态地计算步长,将梯度下降法的矢量编程变为标注编程,虽说增加了计算复杂度,效率相对有所下降,但是在迭代次数上所带来的优化是完全可以弥补其带来的资源开销。来看代码
maxCycles = 1000 # 设置迭代的次数
X = np.hstack([np.ones((len(data), 1)), data])
weights = np.ones(X.shape[1]) # 设置初始的参数,并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。3x1
for j in range(maxCycles):
dataIndex = list(range(len(data)))
for i in range(len(data)):
alpha = 4 / (1.0 + j + i) + 0.0001
randIndex = int(np.random.uniform(0, len(dataIndex)))
vectSum = np.sum(X[randIndex] * weights)
grad = sigmoid(vectSum)
errors = y[randIndex] - grad
weights = weights + alpha * errors * X[randIndex]
del(dataIndex[randIndex])可以对比下梯度下降法,这里多有一次for循环(for i in range(len(data)):),大O必然也增加,但是我们来使用上面对截距,斜率的分析方法看下他们的收敛效果:
截距和斜率变化趋势:
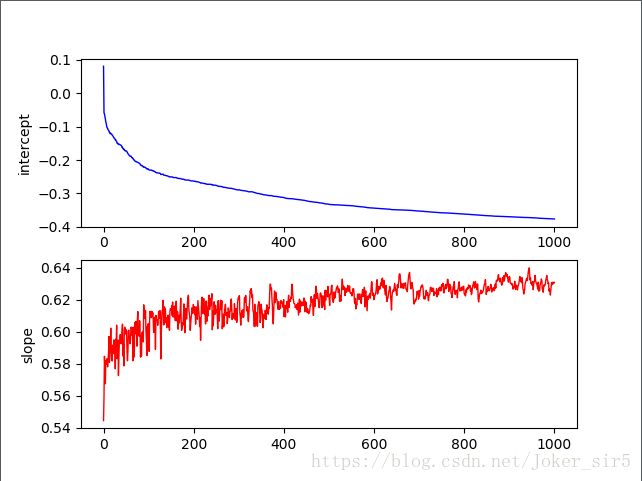
各权重分量weight[0],weight[1],weight[2]的变化趋势:
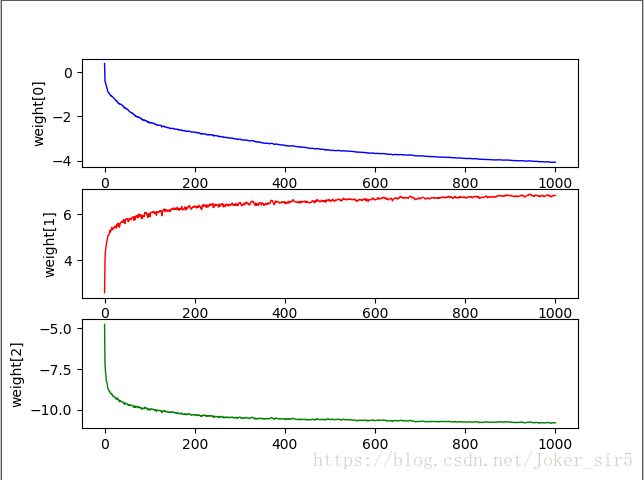
可以看到,在400次迭代之后,随机梯度下降法训练出来的各权重分量变化趋势几乎达到平缓,对比下梯度下降法的变化趋势,在1000次迭代之后各权重分量仍有变化趋势,效果显而易见,在保证准确率的情况下大大提升了收敛的速度,也就平衡了它所带来的计算消耗