ORB特征

本文大部分内容来自ORB特征提取详解，在此基础上加上自己对原论文的理解。

ORB（Oriented FAST and Rotated BRIEF）是一种快速提取特征点和描述子的算法。其特征检测基于FAST，采用BRIEF描述子并加以改进。基于《ORB： an efficient alternative to SIFT or SURF》

1.尺度和旋转不变性的oFAST检测

1.1Fast经典方式提取角点（不具有旋转无关、尺度无关）

第一步，参考文章SIFT角点简介；
第二步：对提取出来的特征点进行Harris特征点检测，检测时设立低阈值，以获得多于N个的fast特征点。
并按照harris的代价函数排序得到最终需要的N个特征值。

1.2尺度无关性

设置一个比例因子scaleFactor（opencv默认为1.2）和金字塔的层数nlevels（pencv默认为8）。将原图像按比例因子缩小成nlevels幅图像。缩放后的图像为：I’= I/scaleFactork(k=1,2,…, nlevels)。nlevels幅不同比例的图像提取特征点总和作为这幅图像的oFAST特征点。

1.3旋转不变性

实现旋转无关性需要为每个特征带一个旋转方向信息。常用的有MAX和BIN的方法，以及ORB的灰度质心方法

BIN:

SIFT中的旋转性是检测特征点邻域内所有像素点的梯度，并构成一个梯度方向直方图（10个或8个柱的直方图），选择最大的柱所对应的梯度范围作为这个特征的主方向。此外还有

MAX

选择特征点邻域内值最大的梯度所对应的方向作为主方向。其效果要比BIN方法稍差。

灰度质心

ORB算法提出使用h灰度质心（intensity centroid） [2] [ 2 ] 来确定FAST特征点的方向。通过计算一个矩来计算特征点以r为半径范围内的质心，特征点坐标到质心形成一个向量作为该特征点的方向。
一个图像块（比如5x5的图像块中），对应的2x2的矩的元素表达为：

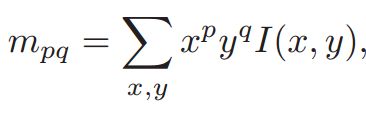
而该图像窗口的质心就是：

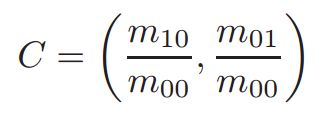
那么整个窗口的旋转为：

其中 θ∈(−\PI,\PI] θ ∈ ( − \PI , \PI ]
其中，I(x,y)为图像灰度表达式，x与y属于区间[-r,r],r为图像块半径，可知质心接近与零点

当p=q=0时，m00是该图像块的灰度和。当这幅图是二进制图像时，m00是该图的面积。

如果将图像的灰度值看做重量，那么质心就是幅图的质心；即整个灰度值的加权中心。

聚ORB论文 [1] [ 1 ] ，灰度质心方法要比BIN与MAX都好

2.rBRIEF描述子

rBRIEF特征描述是在BRIEF特征描述的基础上加入旋转因素。下边先介绍BRIEF，再介绍rBRIEF.

2.rBRIEF描述子

rBRIEF特征描述是在BRIEF特征描述的基础上加入旋转因素。下边先介绍BRIEF，再介绍rBRIEF.

2.1 BRIEF描述子生成原理

简单地说，BRIEF是在一个特征点的邻域选择n对像素点(p,q)，比较其灰度值大小，如果I(p)>I(q)，则令其对应的值为1，否则为0，这样对n对像素比较之后，就形成一个长度为n的二进制向量。一般一般n取128、256或512，opencv默认为256。

这n个点对如何选取呢?

为了增强抗噪性，一般会先对图像进行高斯平滑。ORB算子采用5x5的子窗口进行平滑.
在点周围选取点对I(p,q)的方法有以下5种：

1）在图像块内平均采样；
2）p和q都符合(0,S2/25)的高斯分布；
3）p符合(0,S2/25)的高斯分布，而q符合(0,S2/100)的高斯分布；
4）在空间量化极坐标下的离散位置随机采样；
5）把p固定为(0,0)，q在周围平均采样。
BRIEF作者采用的是第二种。而ORB作者没有选择以上任意方式，而是使用统计学习的方法来重新选择点对集合

BRIEF实时性较好，其原文生成512个描述子用时8.18ms，匹配仅需2.19秒
BRIEF对于旋转过大时，比如超过30度时，匹配正确率迅速下降直到45度时为0。
因此需要对其进行改进：

2.2steered BRIEF(转向的BRIEF，即加入旋转不变性)

在使用oFast算法计算出的特征点中包括了特征点的方向角度。假设原始的BRIEF算法在特征点f的SxS（一般S取31）邻域内选取n对点集D, Di=(xi,yi) D i = ( x i , y i )
f对应的旋转是θ，因此对以上点经过旋转角度θ旋转(不过我猜想此处应该处理成-θ，因为θ在(-PI,PI]之间，那么应该将所有角度旋转到x轴正方向)，得到新的点对：

在新的点集位置上比较点对的大小形成二进制串的描述符
需要注意的是需要对每一金字塔层的图像都进行如此的描述子计算；此外，ORB中角度θ取离散值，360度离散成30份，12度范围内对应一个离散值。

2.3rBRIEF改进BRIEF可区分性

2.3.1steered BRIEF可区分性问题

steered BRIEF加入了旋转不变性，但同时特征描述量的可区分行就下降了。可区分是指该描述量的独特性和不易重复程度，即两个完全不一样的特征不容易产生相似的描述量。
ORB论文中，作者用不同的方法对100k个特征点计算二进制描述符，对每个描述符的均值进行统计，如下表所示：

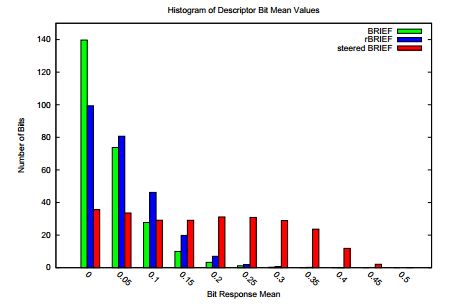
如果描述量中0,1的数量差别不大，那么该描述量均值大概为0.5，整个样本具有最大的方差0.25。其均值离0.5越远，表示描述量中含有更多的1，如steered BRIEF，意味着整个样本的方差越小；简单地讲，如果两个描述量大部分都是1，那么这两个描述量就更容易匹配成功。对于所有的描述量都存在这个趋势的话，描述量都更容易匹配，那么这些描述量的可区分行就降低了，同时也增大了描述符之间的相关性。

为了解决描述子的可区分性和相关性的问题，ORB论文中采用了一种学习好的二进制特征的思路。

原文用来证明steered BRIEF相关性大的方法两种方法：
1.PCA分解矩阵得到特征值并从大到小排序，其中BRIEF 和rBRIEF 的特征值在前十几个特征值后迅速下降，steered BRIEF的特征值却比较均匀；
2.局外点和局内点各自的描述子距离（两描述子的1-范式）两种方法。

2.3.2 rBRIEF（通过学习的方法来选则256维特征向量）

ORB没有使用BRIEF 5种选取点对方法中的任意一种，而是使用统计学习的方法来重新选择点对集合。
对于测试集中的每个点，从31x31的邻域内形成描述子

这里在对图像进行高斯平滑之后，使用邻域中的某个点的5x5邻域灰度平均值来代替某个点对的值。在31x31的邻域内,经过高斯平滑后，可采样的点共有(31-5+1)x(31-5+1)=729个，那么取点对的方法共有M=729*(729-1)/2 = 265356种，我们就要在这Ｍ种方法中选取256种取法，使得用这256维描述量生成的描述子代表整个样本时，每个描述子之间相关性最小。文中采用了一种降低相关系数的方法来选择：

1）先用最长的描述向量描述每个特征点，即对特征点周围区域内所有点（注意此处的点经过高斯平滑，其实只有729个）两两进行比较，共可形成M维度的特征向量。每个元素为1或0。

这个特征向量应该是最优区分能力的，可惜效率太低。因此考虑对它进行降维。

2）将所有300k个特征点进行上述提取，得到Q矩阵，Q的大小为：300k x M。每一列表示300k个特征值在某一维度上的描述。对Q矩阵的每一列求取平均值，按照平均值到0.5的距离大小重新对Q矩阵的列向量排序，形成矩阵T。

此时前边的表示总体而言该维度的可区分行最好。

但假如只是依次将第一列，第二列，第256列就作为特征描述量，可能会出现第一列，第二列实际上是非常相关的情况（比如只差一个系数）。因此需要使得选择的列不仅区分性好而且相互之间相对独立：

3）将T的第一列向量放到R中。
4）取T的下一列向量和R中的所有列向量计算相关性，如果相关系数小于设定的阈值，则将T中的该列向量移至R中。（此处计算相关性的原因）
5）按照4）的方式不断进行操作，直到R中的向量数量为256。

这种方法能降低每一列对所有可能选择的相关程度，相关程度越小，可区分性越大。

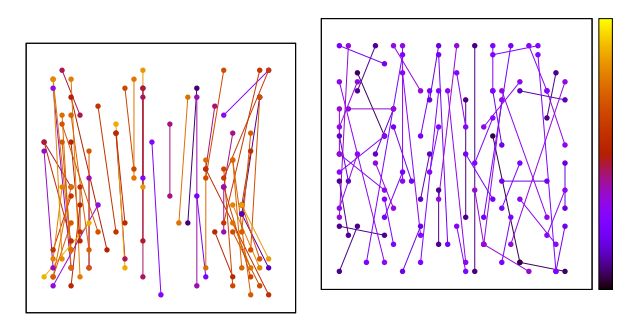
左图是未经学习的点对选取结果，右图是经过学习后选取的点对。

部分源码分析摘记

orb代码简单好读，但起初看到关于点对选取和学习的部分却不容易理解，特摘记如下：

///<该数组存储的是通过学习后选取的256个点对（512点）相对(特征点）的位置，bit_pattern_31_中每四个元素分别表示pair_l.x，pair_l.y,pair_r.x,pair_r.y;
///<共256个点对,产生256维描述子,256维度描述子长度共32个字节。
bit_pattern_31_[256*4] = {
 8,-3, 9,5/*mean (0), correlation (0)*/,
......
    }

//....
float angle = (float)kpt.angle*factorPI;
    float a = (float)cos(angle), b = (float)sin(angle);

    const uchar* center = &img.at(cvRound(kpt.pt.y), cvRound(kpt.pt.x));
    const int step = (int)img.step;

#define GET_VALUE(idx) \       ///<取旋转后一个像素点的值  
    center[cvRound(pattern[idx].x*b + pattern[idx].y*a)*step + \  
               cvRound(pattern[idx].x*a - pattern[idx].y*b)]  
// 循环32次，pattern取值16*32=512,也即每次取16个点，共形成8个点对，8个点对比较可以形成8bit（1 byte）长度的特征描述数据
    for (int i = 0; i < 32; ++i, pattern += 16)
    {
         int t0, t1, val;
         t0 = GET_VALUE(0); t1 = GET_VALUE(1);
         val = t0 < t1;
         t0 = GET_VALUE(2); t1 = GET_VALUE(3);
         val |= (t0 < t1) << 1;
         t0 = GET_VALUE(4); t1 = GET_VALUE(5);
         val |= (t0 < t1) << 2;
         t0 = GET_VALUE(6); t1 = GET_VALUE(7);
         val |= (t0 < t1) << 3;
         t0 = GET_VALUE(8); t1 = GET_VALUE(9);
         val |= (t0 < t1) << 4;
         t0 = GET_VALUE(10); t1 = GET_VALUE(11);
         val |= (t0 < t1) << 5;
         t0 = GET_VALUE(12); t1 = GET_VALUE(13);
         val |= (t0 < t1) << 6;
         t0 = GET_VALUE(14); t1 = GET_VALUE(15);
         val |= (t0 < t1) << 7;

         desc[i] = (uchar)val;//一共32*8维描述子
    }

reference:
1.ORB特征提取详解
2.P. L. Rosin. Measuring corner properties. Computer Vision and Image Understanding, 73(2):291 – 307, 1999.
3.M. Calonder, V. Lepetit, C. Strecha, and P. Fua. Brief: Binary robust independent elementary features. In In European
Conference on Computer Vision, 2010. 1, 2, 3, 5
4.ORB: an efficient alternative to SIFT or SURF
5.ORB源码解析