递推数列的计算

利用递归函数

我们最熟悉的一个递推数列就是斐波那契数列。$1,1,2,3,5,8,13,21,...$，斐波那契数列规定数列的第一个元素和第二个元素都为1，后面的元素是前两个元素之和，可以利用递推公式描述如下：

$F(n)=\{\begin{array}{ll}1& n=1orn=2\\ F(n-1)+F(n-2)& n>=3\end{array}$

根据斐波那契数列的递推公式，我们可以很快写出一个递归函数来计算$F(n)$。伪代码如下：

F(n)
    if n == 1 or n == 2
        return 1
    if n >= 3
        return F(n-1) + F(n-2)

同样，对于其他的递推数列，只要给出了递推公式，我们就能根据递推公式写出一个递归函数。例如有如下递推数列$a_n$，其中$a_1=1$，$a_2=2$，$a_{n+2}=3a_{n-1}-2a_n$，这个递推数列的递推公式如下

$F(n)=\{\begin{array}{ll}1& n=1\\ 2& n=2\\ 3F(n-1)-2F(n-2)& n>=3\end{array}$

F(n)
    if n == 1
        return 1
    if n == 2
        return 2
    if n >= 3
        return 3 * F(n-1) - 2 * F(n-2)

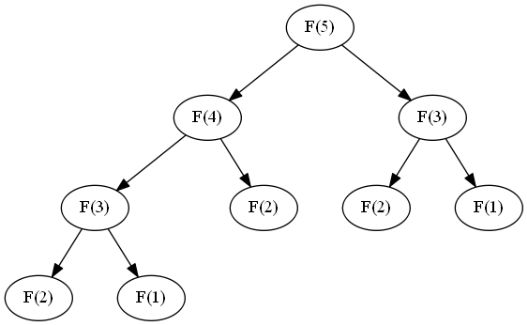
利用递归函数求解递推数项非常简单，但是计算效率很低，时间复杂度为$O(2^n)$，存在大量的重复计算。以斐波那契数列$n=5$为例调用$F(n)$，计算$F(5)$需要计算$F(3)$和$F(4)$，在计算$F(4)$需要计算$F(3)$和$F(2)$，这里$F(3)$就被重复计算了，当$n$的值很大的时候，这个重复计算的值就非常多了。

利用动态规划

为了避免重复计算，我们可以使用动态规划来计算递推数列，同样是以我们最熟悉的斐波那契数列为例。从第三个数开始，每一个数只依赖于前两个数，我们可以保存前两个数，在每计算一个数后，更新这两个数。伪代码如下：

F(n)
    if n >= 1:
        a = 0
        b = 1
        for i = 1 to n
            a, b = b, a+b
        return a

利用动态规划来求解递推数列相比直接使用递归函数来说优化了不少，时间复杂度为$O(n)$，其中每一个数最多只会计算一次。

利用矩阵快速幂

同样使用斐波那契数列为例子，我们把结果项构造成$1\times 2$的矩阵$\left[\begin{array}{cc}F(n)& F(n-1)\end{array}\right]$，为了得到这个矩阵，我们可以利用初始矩阵乘以转置矩阵来获得。我们假设已经知道了初始矩阵$\left[\begin{array}{cc}F(n-1)& F(n-2)\end{array}\right]$，根据公式$\left[\begin{array}{cc}F(n)& F(n-1)\end{array}\right]=\left[\begin{array}{cc}F(n-1)& F(n-2)\end{array}\right]\times \left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$，我们可以计算出转置矩阵$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]$。

有了转置矩阵后，我们可以直接通过矩阵运算来计算出最后的结果项。$\left[\begin{array}{cc}F(n)& F(n-1)\end{array}\right]=\left[\begin{array}{cc}F(n-2)& F(n-3)\end{array}\right]\times {\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]}^2$，最后，我们可以直接通过初始项$\left[\begin{array}{cc}1& 1\end{array}\right]$乘以转置矩阵的$n-2$次方来构造出斐波那契数列的结果项。$\left[\begin{array}{cc}F(n)& F(n-1)\end{array}\right]=\left[\begin{array}{cc}1& 1\end{array}\right]\times {\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]}^{n-2}$。

在这里，我们的置换矩阵是$2\times 2$是由于斐波那契数列是一个二维递推数列。通俗地讲，如果一个递推数列的任意项是可以由最原始的前$k$个数递推出来，那么这个递推数列就是$k$维的。斐波那契数列的任意一项都是从$F(1)，F(2)$推出来的，所以斐波那契数列是二维递推数列。假设现在有一个递推数列$a_1=1,a_2=1,a_3=1,a_{n+3}=a_n+a_{n+2}$，这个递推数列就是三维的。所以一个$k$维的递推数列结果项可以这样构造

$\left[\begin{array}{ccc}F(n)& ...& F(n-k+1)\end{array}\right]=\left[\begin{array}{ccc}F(k)& ...& F(1)\end{array}\right]\times {\left[\begin{array}{ccc}{a}_{11}& ...& a_{1k}\\ ...& ...& ...\\ a_{k1}& ...& a_{kk}\end{array}\right]}^{n-k}$

在计算转置矩阵的幂$A^n$的时候可以利用矩阵快速幂来计算。假设这里的$n=8$，按照常规计算方法需要进行8次矩阵乘法运算。但是我们可以通过计算$A\times A$得到$A^2$，再通过$A^2\times A^2$得到$A^4$，最后通过$A^4\times A^4$得出结果，这里只需要三次矩阵乘法。所以利用矩阵快速幂可以将求解递推数列的时间代价下降到$O(\lg n)$。