点-双连通分量&边-双连通分量复习笔记

之前一直搞不清楚点双连通分量和边双连通分量，于是花了一个晚上专门搞双连通分量的概念和相关的题。
【有些东西不准确还望大佬们指正

点双连通分量

概念：如果任意两点至少存在两条“点不重复”的路径，就说这个图是点-双连通分量。等价于内部无割顶（割点）。
一个点双连通分量：

两个点双连通分量：

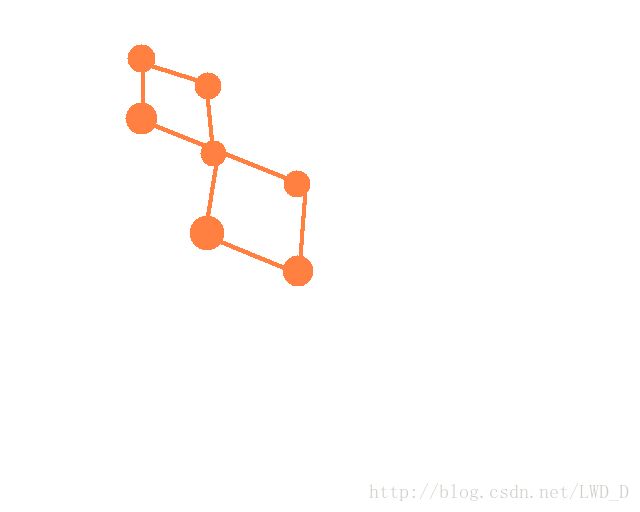
（中间那个为割点）

poj1144求割顶数量模板题：

#include
#include
#include
using namespace std;
const int N=1e2+5,M=1e4+5;
int to[M],nxt[M],head[N],etot;
int dfn[N],low[N],idc,cnt;
bool iscut[N];
void adde(int u,int v)
{
    to[++etot]=v;
    nxt[etot]=head[u];
    head[u]=etot;
}
void tarjan(int u,int fa)
{
    int son=0;
    low[u]=dfn[u]=++idc;
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            son++;
            if(low[v]>=dfn[u]&&u!=fa) iscut[u]=1;
        }else 
            low[u]=min(dfn[v],low[u]);

    }
    if(u==fa&&son>1) iscut[u]=1;
}
void init()
{
    etot=0;idc=0;cnt=0;
    memset(iscut,0,sizeof(iscut));
    memset(head,0,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
}
int main()
{
    int n;
    while(scanf("%d",&n)&&n){
        init();
        int u,v;
        while(scanf("%d",&u)&&u){
            while(getchar()!='\n')
            {
                scanf("%d",&v);
                adde(u,v);
                adde(v,u);
            }
        }
        tarjan(1,1);
        for(int i=1;i<=n;i++)
        if(iscut[i]) cnt++;
        printf("%d\n",cnt);
    }
    return 0;
}

求点双连通分量
这个比较特殊因为它要用边入栈！！
以及实在是找不到裸题了，【也不知道这个板子对不对】

#include
#include
#include 
using namespace std;
const int N=100,M=100;
int dfn[N],low[N],cnt,iscut[N],idc;
int head[N],nxt[M],to[M],etot;
typedef pair<int,int> pii;
stack stk;
void dfs(int u,int fa)
{
    low[u]=dfn[u]=++idc;
    int son=0;
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        if(!dfn[v]){
            stk.push(make_pair(u,v));
            son++;
            dfs(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                iscut[u]=1;
                cnt++;
                while(1){
                    pii e=stk.top();stk.pop();
                    /*一些缩点操作*/
                    if(e.first==u&&e.second==v) break; 
                }
            }
        }
        else {
            stk.push(make_pair(u,v));
            low[u]=min(low[u],dfn[v]);
        }
    }
}
int main()
{

}

以下是ywq大佬的板子
【保证正确啦】

void tarjan(int u,int f){
    dfn[u]=low[u]=++indx;
    for(int i=head[u];i;i=e[i].pre){
        int v=e[i].v;
        if(v==f) continue;
        if(vis[i]) continue;
        vis[i]=vis[i^1]=true;//亲测vis数组是必需的 
        s.push(i);
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                ++cnt;iscut[u]=true;
                while(1){
                    int t=s.top();s.pop();
                    col[e[t].u]=cnt,col[e[t].v]=cnt;
                    if(t==i) break;
                }
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}

边双连通分量

概念：如果任意两点至少存在两条“边不重复”的路径，就说这个图是边-双连通分量。即所有边都不是桥。
一个边双连通分量：

两个边双连通分量：

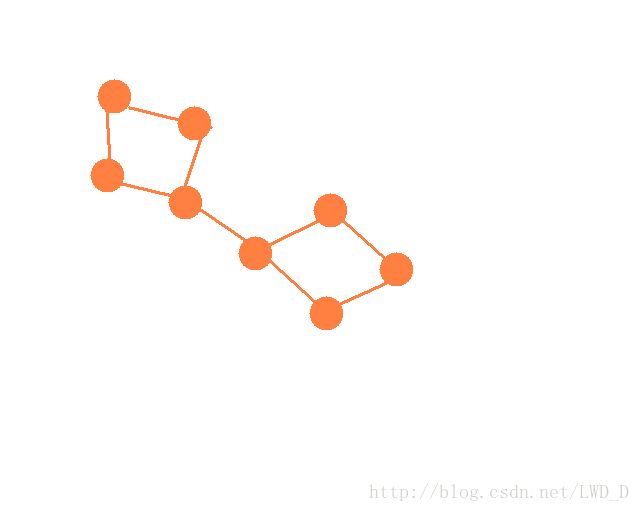
（中间的那条边为桥）

求桥（割边）：（没有找到模板题，和求割顶原理差不多，少了一个=）

    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) 
                isbridge[i]=1;
        }else 
        low[u]=min(low[u],dfn[v]);
    }

poj3177求边双连通分量模板题

/*
法一：
入栈和强连通分类似

法二：
for(int u=1;u<=n;u++)
for(int i=head[u];i;i=nxt[i]){
    int v=to[i];
    if(low[v]!=low[u]) in[low[v]]++,in[low[u]]++;
} 
之前是用了一个栈来判别哪些点位于一个边双连通分量中， 这个就直接用low了
为什么是正确的？
如果一个点v的low[v]
#include
#include
#include
using namespace std;
const int N=5000+5,M=2e4+5;
int n,m;
int nxt[M],head[N],to[M],etot;
bool exi[N][N];
int low[N],dfn[N],idc,stk[N],top;
int belong[N],num,in[N];
void adde(int u,int v)
{   
    to[++etot]=v;
    nxt[etot]=head[u];
    head[u]=etot;
}
void tarjan(int u,int fa)
{
    low[u]=dfn[u]=++idc;
    stk[++top]=u;
    for(int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa) continue;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }else 
        low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        num++;
        while(1){
            int x=stk[top--];
            belong[x]=num;
            if(x==u) break;
        }
    }
}
void init()
{
    etot=0;idc=0;num=0;
    memset(head,0,sizeof(head));
    memset(exi,0,sizeof(exi));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(belong,0,sizeof(belong));
    memset(in,0,sizeof(in));
}
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF){
        init();
        for(int i=1;i<=m;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            if(!exi[u][v]){
                adde(u,v),adde(v,u);
                exi[u][v]=exi[v][u]=1;
            }
        }
        tarjan(1,1);
        for(int u=1;u<=n;u++)
        for(int i=head[u];i;i=nxt[i]){
            int v=to[i];
            if(belong[v]!=belong[u]) in[belong[v]]++,in[belong[u]]++;
        }
        int cnt=0;
        for(int i=1;i<=num;i++)
        if(in[i]==2) cnt++;
        printf("%d\n",(cnt+1)/2);
    }

    return 0;
}