Tensorflow学习笔记:基础篇(3)——Mnist手写集初始版本
Tensorflow学习笔记:基础篇(3)——Mnist手写集初始版本
前序
— MNIST 手写数据集,作为一个经典的数据集,已经被大家所“嚼烂”, 无论是初学者还是高手,几乎都会用到它,网上的版本也是多种多样,绝大多是都是用CNN,因为公认速度快、识别准,当然对于初学者,显然一开始并不能理解CNN,更别说去运用它。
— 我将以一个初学者的角度,基于前两篇博文已经搭好的框架的基础上,通过几篇博文,运用多种方法,从最傻最笨的全连接法到最后牛逼的CNN法,期间穿插Tensorboard的使用和多种优化器的选择,深入浅出的手把手教大家进行MNIST数据集的学习。
MNIST数据集
Reference:极客学院官方文档
基于官方文档的内容,我大概提炼几个重要的知识点
数据集安装
MNIST数据集的官网是Yann LeCun’s website。当然,你也可以通过下面这行代码,实现自动下载和安装,第一次执行程序可能需要花费些时间下载数据集,之后将不再需要,可以直接执行。
import tensorflow.examples.tutorials.mnist.input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)数据集内容
下载下来的数据集被分成两部分:60000行的训练数据集(mnist.train)和10000行的测试数据集(mnist.test)。
每一个MNIST数据单元有两部分组成:一张包含手写数字的图片和一个对应的标签。我们把这些图片设为“xs”,把这些标签设为“ys”。
每一张图片包含28X28个像素点。我们可以用一个数字数组来表示这张图片:

我们把这二维矩阵展开成一个一维向量,长度是 28x28 = 784。
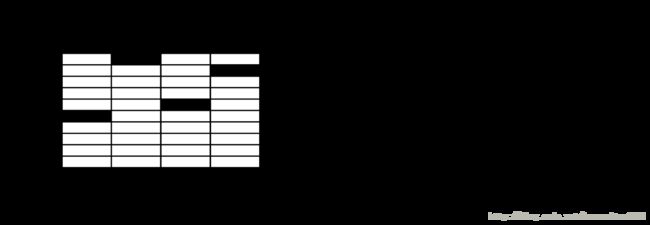
这样,在MNIST训练数据集中,训练数据集图片(mnist.train.images) 是一个形状为 [60000, 784] 的张量,第一个维度数字用来索引图片,第二个维度数字用来索引每张图片中的像素点。在此张量里的每一个元素,都表示某张图片里的某个像素的强度值,值介于0和1之间。

你可以把这个 [60000, 784]张量,想象成上图那样,6w张图片这样一片一片的按序排列,每张图都有784个像素点,故此构成这个二维矩阵。
之前我们说的都是每张图片(即:xs),现在我们来说说标签(即:ys)
相对应的MNIST数据集的标签是介于0到9的数字,用来描述给定图片里表示的数字。我们定义标签数据是”one-hot vectors”。 一个one-hot向量除了某一位的数字是1以外其余各维度数字都是0。所以在此教程中,数字n将表示成一个只有在第n维度(从0开始)数字为1的10维向量。比如,标签0将表示成([1,0,0,0,0,0,0,0,0,0,0])。因此,训练数据集标签(mnist.train.labels)是一个 [60000, 10] 的数字矩阵。
Softmax函数
用来给不同的对象分配概率(通常放在分类网络的最后一层),具体的数学推导公式,详见Reference。
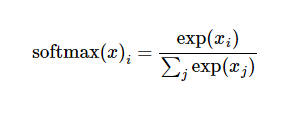
接下来,我们来实现一个非常简单的两层全连接网络来完成MNIST数据的分类问题,输入层784个神经元,对应每张图片784个像素点;输出层10个神经元,对应0-9这10个数字,实现分类。

计算流程
1、数据准备
2、准备好placeholder
3、初始化参数/权重
4、计算预测结果
5、计算损失值
6、初始化optimizer
7、指定迭代次数,并在session执行graph
代码示例
1、数据准备
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 载入数据集
mnist = input_data.read_data_sets("MNIST_data", one_hot=True)
# 每个批次送100张图片
batch_size = 100
# 计算一共有多少个批次
n_batch = mnist.train.num_examples // batch_size2、准备好placeholder
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])3、初始化参数/权重
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))4、计算预测结果
因为只有输入和输出两层神经网络,之前说过softmax放在分类的最后一层,所以这里直接上softmax
prediction = tf.nn.softmax(tf.matmul(x, W) + b)5、计算损失值
这里我们先使用二次代价函数(先不使用交叉熵函数,不然怎么做对比,突出交叉熵函数的好呢~~~)
loss = tf.reduce_mean(tf.square(y - prediction))6、初始化optimizer
GradientDescentOptimizer优化器,学习率建议给的稍大一些
learning_rate = 0.2
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 结果存放在一个布尔型列表中
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(prediction, 1))
# argmax返回一维张量中最大的值所在的位置,还记得之前讲的label吗~~([1,0,0,0,0,0,0,0,0,0,0]),agrmax返回的就是1所在的位置,如果预测值与所给的标签集相同,表示成功识别数字,返回值为1,反之为0
# 求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))7、指定迭代次数,并在session执行graph
init = tf.global_variables_initializer()
sess.run(init)
再次强调!!!此处两句极其重要,需要先初始化变量,才能进行读取和写入(赋值)操作
n_sample = xs.shape[0]
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for epoch in range(21):
for batch in range(n_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys})
acc = sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels})
if epoch % 2 == 0:
print("Iter " + str(epoch) + ",Testing Accuracy " + str(acc))
运行结果
迭代计算20次,准确率0.91左右,这个准确率是比较低的,还有很大的提升空间,那么我们做什么修改就能提升准确率呢,具体我将在接下来的文章中进行。

这里先给几个提示:
(1)增加神经网络的层数,我们现在只有输入输出层,尝试添加隐藏层试试呢~~
(2)尝试将二次代价函数修改成交叉熵函数呢~~
(3)尝试多选几个梯度下降优化器呢~~
完整代码
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 载入数据集
mnist = input_data.read_data_sets("MNIST_data", one_hot=True)
# 每个批次的大小
batch_size = 100
# 计算一共有多少个批次
n_batch = mnist.train.num_examples // batch_size
# 定义两个placeholder
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])
# 创建一个简单的神经网络
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x, W) + b)
# 二次代价函数
loss = tf.reduce_mean(tf.square(y - prediction))
# 使用梯度下降法
optimizer = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
# 初始化变量
init = tf.global_variables_initializer()
# 结果存放在一个布尔型列表中
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(prediction, 1)) # argmax返回一维张量中最大的值所在的位置
# 求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
sess.run(init)
for epoch in range(21):
for batch in range(n_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys})
acc = sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels})
if epoch % 2 == 0:
print("Iter " + str(epoch) + ",Testing Accuracy " + str(acc))