PRML读书笔记(三)

回归的目标是在给定输入的情况下，预测具有连续性质的目标值。线性回归中的线性是相对于参数而言的。

3.1 线性基函数模型(Linear Basis Function Models)

最简单的线性回归模型是： y(x,w)=w0+w1x1+⋯+wDxD ，很明显这个模型不足以表达复杂的模型，但是我们能够从这个模型中得出线性回归模型的一般形式

y(x,w)=w0+∑j=1Mwjϕj(x)(1)

其中 ϕj(x) 即基函数，该函数可以是任意的函数，一般为非线性函数(为了提高模型的表达能力)； w0 为偏置，假设我们令 ϕ0(x)=1 ，那么上式就可以简化成

y(x,w)=∑j=0Mwjϕj(x)=wTϕ(x)

整个模型对于输入是非线性的，而对于参数是线性的，这样就在提高模型表达能力的同时，也简化了模型。但是这种简化也导致了明显的限制，后面会详细介绍。

第一章中的曲线拟合，我们令 ϕj(x)=xj ，多项式基函数是输入变量的全局函数，如果一个输入变量的区域改变会影响其他的输入区域，比如 (2,1,1,1)→(2,1,1,9) ，但是如果采用如高斯基函数等局部函数的话，就不会出现这种情况。

常见的几类基函数:
1. 多项基函数： ϕj(x)=xj
2. 高斯基函数： ϕj(x)=exp{−(x−μj)22s2}
3. sigmoid： ϕj(x)=σ(x−μjs),σ(a)=11+exp(−a)

3.1.1 最大似然和最小二乘法

假设目标值t由判别函数与一个额外的噪声给出: t=y(x,w)+ϵ ， 其中噪声为一个均值为0、精度为 β 的高斯噪声。那么

p(t|x,w,β)=N(t|y(x,w),β−1)

假设我们令其损失函数为平方损失函数(square loss function)，那么最优预测值就与条件均值一致

E[t|x]=∫tp(t|x)dt=y(x),w))

其中 p(t|x)=p(t|x,w,β) 。需要注意的是高斯噪声假设隐含t在给定x的条件分布是单峰的，这个性质可能对于某些应用不太合适。作为扩展，我们可以采用混合高斯分布。

X={x1,…,xN} ，其对应的值为 t={t1,…,tN} ，那么

p(t|X,w,β)=∏n=1NN(t|y(xn,w),β−1)

为了使公式保持整齐，我们可以将上式写成

p(t|w,β)lnp(t|w,β)ED(w)===∏n=1NN(t|wTϕ(xn),β−1)N2lnβ−N2ln2π−βED(w)12∑n=1N{tn−wTϕ(xn)}2

要使 p(t|w,β) 最大，那么

00⇒wMLΦ====∂lnp(t|w,β)∂w∑n=1N{tn−wTϕ(xn)}ϕ(xn)T(ΦTΦ)−1ΦTt⎡⎣⎢⎢⎢⎢⎢ϕ0(x1)ϕ0(x2)⋮ϕ0(xN)⋯⋯⋱⋯ϕM−1(x1)ϕM−1(x2)⋮ϕM−1(xN)⎤⎦⎥⎥⎥⎥⎥

如果我们将偏置参数 w0 提出来，那么

ED(w)⇒w0==12∑n=1N⎧⎩⎨tn−w0−∑j=1M−1wjϕj(xn)⎫⎭⎬21N∑n=1Ntn−∑j=1M−1wj{1N∑n=1Nϕj(xn)}

由上面公式我们可以看出，偏置参数 w0 补偿平均目标值与基函数加权平均值的差异。

1βML=1N∑n=1N{tn−wTMLϕ(xn)}2

我们可以得到预测值与噪声的精度无关，但噪声的精度可以作为衡量预测值与目标值差异的一个标准。

3.1.2 最小二乘的几何形状

首先考虑坐标轴为 tn 的N维空间，那么 tn={t1,…,tN}T 就是这个空间里的一个向量。那么 φj={ϕj(x1),…,ϕj(xN)}T 也是N为空间里的向量。 y={y(x1,w),…,y(xN,w)}T

如果基函数的数量 M 小于训练数据集的数量 N ，那么我们可以找到一个M维的子空间 S 来表示 φj ，而 y 是 φj 向量的任意线性组合，所以 y 可以落在M维子空间 S 的任意位置上。 所以最小二乘法的解就变成了 t 在子空间 S 的投影。

3.1.3 顺序学习

最小二乘法的顺序学习可以采用随机梯度下降法

wτ+1wτ+1==wτ−η∇Enwτ+η(tn−wTϕ(xn))ϕ(xn)

3.1.4 正则化的最小二乘法

在第一章中，我们介绍了一种正则化的方法来控制过拟合，即

E(w)ED(w)EW(w)===ED(w)+λEW(w)12∑n=1N{tn−wTϕ(xn)}212wTw

上面的 EW 是比较常见的权值衰减，也可以采用其他的正则化方法。权值衰减的一个优点是保持整个损失函数仍然是权值的二项式。正则化方法会使权值收缩，从而减小噪声的影响。

12∑n=1N{tn−wTϕ(xn)}2+λ2∑j=1M−1|wj|q

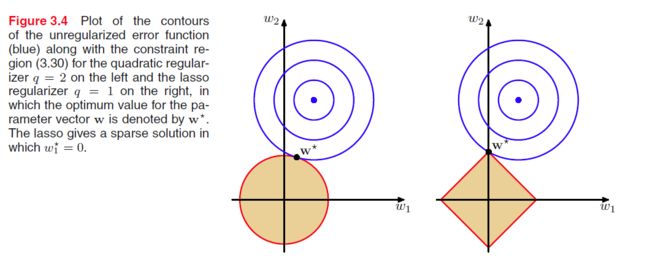
对于上式我们可以将其看成约束条件为 ∑M−1j=1|wj|q≤η 的拉格朗日乘子，那么

由于上图中的损失函数是 w1,w2 的二项式函数，所以为圆形。当 λ 增加时，会驱使更多的权值趋向0。

3.1.5 多个输出值

当有 K 个输出值时，那么权值 W 为MxK的矩阵。之后的分析是一致的。

3.2 Bias-Variance

我们知道如果训练数据集过小，而模型太复杂的话，会导致过拟合现象，但是如果为了减小过拟合现象而限制模型的灵活性，又可能会捕捉不到数据的重要性质。因此我们引入了正则化项，但是如何决定 λ 仍然是个难题。

第一章中我们得到了 E(L) 的表达式，

E(L)h(x)==∫{y(x)−h(x)}2p(x)dx+∫{t−h(x)}2p(x,t)dxdt∫tp(t|x)dt=E[t|x]

上式的 h(x) 是最佳预测，而 y(x) 是实际预测。其中第二项是固有的噪声，第一项跟我们选取的 y(x) 相关，当我们有充足的训练数据的时候 y(x)=h(x) ，但是往往训练数据集是有限的。

如果我们用 y(x,w) 来对 h(x) 建模，在贝叶斯方法中，这个模型的不确定性由 p(w|x) 决定；而对于频率方法来说，需要基于一个特定数据集 D 来对 w 进行估计。对于任意数据集 D ，我们能够得到 y(x;D) ，那么评测一个学习算法的性能时采用对所有数据集的集成平均。

假设我们有一个数据集 D ，则第一项的被积函数可以写成

{y(x;D)−h(x)}2

实际预测值 y(x;D) 相对于 D 的平均值为 ED[y(x;D)] ，那么上式可以写成

ED[{y(x;D)−h(x)}2]=+={y(x;D)−ED[y(x;D)]+ED[y(x;D)]−h(x)}2{y(x;D)−ED[y(x;D)]}2+{ED[y(x;D)]−h(x)}22{y(x;D)−ED[y(x;D)]}{ED[y(x;D)]−h(x)}{ED[y(x;D)]−h(x)}2(bias)2+ED[{y(x;D)−ED[y(x;D)]}2]variace

h(x) 是最佳预测不依赖于 D 。偏置(bias)项表示平均值与最佳预测值的差异，方差(variance)表示了个体数据与平均值的震荡程度，即 y(x;D) 对于特殊的数据集敏感度。因此期望平方差可以写成

expected lossbias2variancenoise====bias2+variance+noise∫{ED[y(x;D)]−h(x)}2p(x)dx∫ED[{y(x;D)−ED[y(x;D)]}2]p(x)dx∫{h(x)−t}2p(x,t)dxdt

由于噪声是固有的，因此我们只能优化bias和variance，对于灵活(flexible)模型有较小的偏置极大方差，对于相对刚性(rigid)的模型具有较大的偏置和较小的方差。

p(t|x,w,β)=N(t|y(x,w),β)

这个图在方差方面不太直观，可以参考第一章图1.4.

尽管从频率观点上，bias-variace分解能够提供一些有趣(interesting)的见解，但是它是基于对集成数据集上的，而在实际中我们只有一个数据集。如果我们有一系列数据集，合并成一个数据集也可以减小过拟合现象。

3.3 贝叶斯线性回归

贝叶斯方法能够避免最大似然方法导致的过拟合现象，并且在只使用训练数据的情况下自动决定模型的复杂性。

3.3.1 参数分布

第二章中我们介绍了在贝叶斯方法中最重要的是共轭先验，在线性回归中我们知道似然函数为 p(t|w,β)=∏Nn=1N(t|wTϕ(xn),β−1) 是关于 w 二项式的指数函数，那么共轭先验是

p(w)p(w|t)mNS−1N====N(w|m0,S0)N(w|mN,SN)SN(S−10m0+βΦTt)S−10+βΦTΦ

上述后验概率的推导可以利用 completing the square方法得出。由于后验概率是高斯分布，因此它的模(mode)即均值(mean)，所以 wMAP=mN 。如果 S0=α−1I ，当 α→0 时，先验概率就表示对整个空间上的参数没有偏向，那么 mN 就变成了 wML 。

考虑一个特殊共轭先验 p(w|α)=N(w|0,α−1I) ，那么

mNS−1N⇒lnp(w|t)===βSNΦTtαI+βΦTΦ−β2∑n=1N{tn−wTϕ(xn)}2−α2wTw+const

从 lnp 可以看到权值衰减的平方差损失函数符合贝叶斯思想。

3.3.2 预测分布

但是需要注意到是到目前为止，还是进行了点估计，上面的方法又叫做model selection，即选择后验概率最大的模型；下面我们介绍model averaging，即将多个模型加权平均从而得到预测分布。给定一个新的输入 x 预测它的值 t ，

p(t|t,α,β)p(t|w,β)p(w|t,α,β)===∫p(t|w,β)p(w|t,α,β)dwN(t|wTϕ(x),β−1)N(w|mN,SN)

上面的公式为了简化概念，省略了 t 相对应的输入值

p(x)p(y|x)⇒p(y)⇒p(t|x,t,α,β)σ2N(x)=====N(x|μ,Λ−1)N(y|Ax+b,L−1)N(y|Aμ+b,L−1+AΛ−1AT)N(t|mTNϕ(x),σ2N(x))1β+ϕ(x)TSNϕ(x)

σ2N(x) 的第二项表示相对于参数 w 的不确定性，当 N→∞ 时，第二项趋向于0。

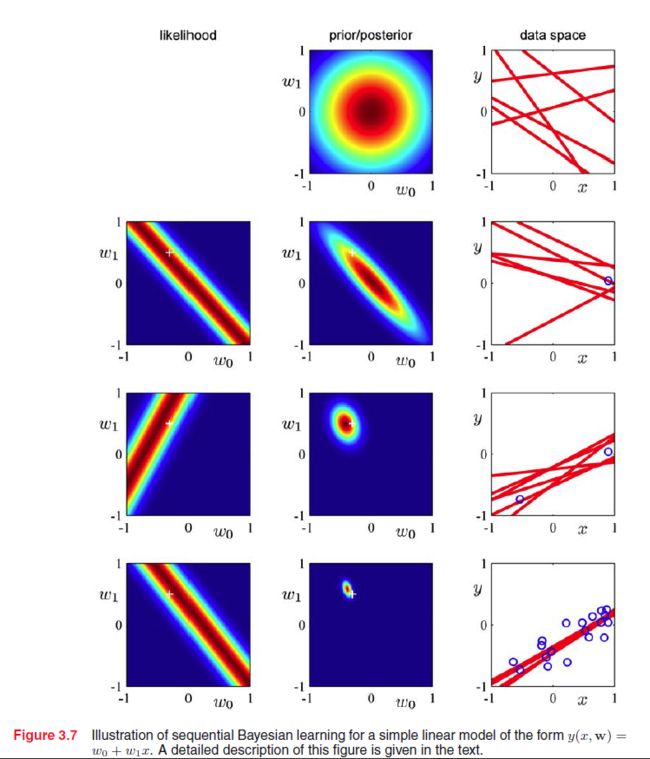
从上图我们可以看出预测的不确定性依赖于 x ，当 x 在训练数据邻近时，不确定性大大降低，而且当训练数据增多时，整体不确定性降低。

下图是从后验概率抽取参数，并且画出它们的曲线

3.3.3 等价核(Equivalent Kernel)

在model selection方法中，加入我们将均值代入到 y(x,w)=wTϕ(x) ，得到

y(x,mN)=mTϕ(x)=βϕ(x)SNΦTt=∑n=1Nβϕ(x)TSNϕ(xn)tn

进一步写成

y(x,mN)k(x,x′)==∑n=1Nk(x,xn)tnβϕ(x)TSNϕ(x′)

上式 k 即equivalent kernel。我们可以将 k(x,xn) 看成 tn 相对应的权值。

weight local evidence more strongly than distant evidence。

cov[y(x),y(x′)]==cov[ϕ(x)Tw,wTϕ(x′)]ϕ(x)TSNϕ(x′)=β−1k(x,x′)

由此我们知道在预测值附近的点高度相关，而对于两个距离比较远的点相关性比较小。

3.4 贝叶斯模型比较

最大似然方法导致的过拟合现象能够通过边缘化(累加或积分)模型的参数而不是对参数进行点估计来避免。假设我们想比较L个模型 {Mi},i=1,…,L 。模型表示对数据集 D 的概率分布。 p(Mi) 表示刚开始我们对这个分布的不确定性，即先验，那么给定一个数据集 D 后，

p(Mi|D)∝p(D|Mi)p(Mi)

p(D|Mi) 是模型的证据(model evidence)，即表示模型被当前数据集的偏向性(preference)，又叫边缘似然(marginal likelihood)。贝叶斯因子： p(D|Mi)/p(D|Mj)

对于model averaging来说

p(t|x,D)=∑i=1Lp(t|x,Mi,D)p(Mi|D)

很明显对于model averaging来说，计算量是一个比较大的限制，因此有时候我们可以用最大后验概率的模型来近似model averaging，这叫做model selection。模型由参数 w 控制，那么

p(D|Mi)=∫p(D|w,Mi)p(w|Mi)dw

Mi 相当于模型的超参数(hyper-parameter)，比如线性回归中基函数与基函数的个数；而 w 则是这个模型学到的参数，很明显在相同的超参数下，参数 w 有多重可能性。

p(w|D,Mi)=p(D|w,Mi)p(w|Mi)p(D|Mi)

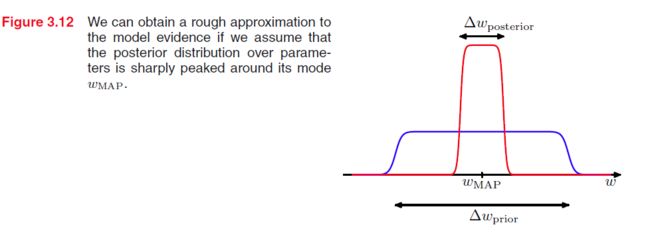
下面我们考虑在模型 Mi 情况下，并且只有一个参数 w ，后验概率 p(w|D)∝p(D|w)p(w) ，假设后验概率分布集中分布在 wMAP ，宽度为 Δwposterior ，假如我们进一步假设先验为 p(w)=1/Δwprior

p(D)⇒lnp(D)=≃∫p(D|w)p(w)dw≃p(D|wMAP)ΔwposteriorΔwpriorlnp(D|wMAP)+ln(ΔwposteriorΔwprior)

第一项表示模型在最大后验对数据的拟合程度；第二项是惩罚项，因为 Δwposterior<Δwprior ，所以这项是负值，并且当模型越复杂时， Δwposterior 就越小，从而使惩罚越重(对于相同的模型 Mi ，惩罚项相同？)。

假设有M个参数，并且所有的参数有相同的比率 Δwposterior/Δwprior ，那么

⇒lnp(D)≃lnp(D|wMAP)+Mln(ΔwposteriorΔwprior)

此时模型的复杂性由M控制，当M增加时，第一项增加，当模型越复杂，它能更好的拟合数据，从而 p(D|wMAP) 增加，故第一项增加；第二项减小，这是因为 ln(ΔwposteriorΔwprior) 为负，故M增加，第二项减小，从而最优解是这两项的平衡点(trade-off)。

由上图我们知道，采用的模型跟数据量的大小有关。

贝叶斯模型能够只用训练数据选择最佳模型(理论上？)，假设我们有两个模型 M1,M2 ，而真实模型为 M1 ，那么

∫p(D|M1)lnp(D|M1)p(D|M2)dD=−∫p(D|M1)lnp(D|M2)p(D|M1)dD

上式为相对熵，表示 M1,M2 的不相似性，明显理论上是可以单单采用训练数据就可以选择正确模型，但是在有多个模型的时候，计算量十分复杂。

3.5 The Evidence Approximation

Fully Bayesian中要求边缘化hyper-parameter，但是这往往是analytically intractable的，因此我们用逼近思想去分析，

p(t|t)=∫∫∫p(t|w,β)p(w|t,α,β)p(α,β|t)dwdαdβ

如果后验分布 p(α,β|t) 集中分布在 α^,β^ 上，那么上式近似于

p(t|t)≃p(t|t,α^,β^)=∫p(t|w,β^)p(w|t,α^,β^)dw

所以现在我们的目标最变成了如何确定 α^,β^ ，由于 p(α,β|t)∝p(t|α,β)p(α,β) ，如果我们对 p(α,β) 没有偏向，那么变成了 p(α,β|t)∝p(t|α,β) ，从而目标变成了求 p(t|α,β)

3.5.1 Evalution of Evidence Function

p(t|α,β)p(t|w,β)p(w|α)⇒p(t|α,β)E(w)=====∫p(t|w,β)p(w|α)dw∑n=1NN(tn|wTϕ(xn),β−1)N(w|0,α−1I)(β2π)N/2(α2π)M/2∫exp{−E(w)}dwβED(w)+αEW(w)=β2∥t−Φw∥2+α2wTw

我们想得到高斯函数的指数形式即 E(w)=12(w−mN)TA(w−mN)+E(mN) ，第二项是与 w 无关的项，根据completing the square方法，我们得到

AmNE(mN)===αI+βΦTΦβA−1ΦTtβ2∥t−ΦmN∥2+α2mTNmN

所以

∫exp{−E(w)}dw⇒lnp(t|α,β)===exp{−E(mN)}∫exp{−12(w−mN)TA(w−mN)}dwexp{−E(mN)}(2π)M/2|A|−1/2M2lnα+N2lnβ−E(mN)−12ln|A|−N2ln2π

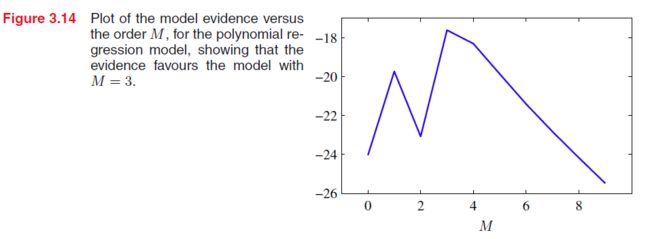
下图是第一章中曲线拟合的model evidence

3.5.2 Maximizing the evidence function

首先我们考虑 p(t|α,β) 相对于 α 的偏导，在这之前我们定义 (βΦTΦ)ui=λiui ，那么 A 的特征值即为 α+λi 。

ddαln|A|⇒0⇒αmTNmN⇒γ⇒α=====ddα∏iln(λi+α)=∑i1λi+αM2α−12mTNmN−12∑i1λi+αM−α∑i1λi+α=γ∑iλiλi+αγmTNmN

需要注意的是 α=γmTNmN 并不是 α 的直接解，因为 γ,mN 都依赖于 α 。我们采用迭代过程来对 α 进行求解，首先任意初始化 α ，然后求 mN=βSNΦTt ，再求 γ ，递归求解 α

同理求 β 的偏导

ddβln|A|⇒1β==ddβ∏iln(λi+α)=1β∑iλiλi+α=γβ1N−γ∑n=1N{tn−mTNϕ(xn)}2

明显也要用迭代过程来对 β 进行求解。而且我们知道 α,β 的值依赖于训练数据。

3.5.3 有效参数的数量

当 α→0 时，此时的模是似然函数的解，而 A=βΦTΦ ，也就是说 λi 是一个参数被数据决定的程度( λi measures how strongly one parameter is determined by the data)。那么 α 就是所有参数被先验决定的程度。 wMAPi=λiλi+αwMLi ，如果 λi≪α ，那么 wi→0 ，即数据对这个参数不敏感，由上面分析可以知道 γi=λiλi+α 能够估量有效参数的数量。

现在我们考虑 β ，在贝叶斯分析中 1βMAP=1N−γ∑Nn=1{tn−mTNϕ(xn)}2 ，而在最大似然估计中 1βML=1N∑Nn=1{tn−wTMLϕ(xn)}2 ，因为在贝叶斯分析中的参数有效数量取决于 γ ，因此要补偿最大似然估计从而使其无偏。

当 N≫M 时， r=M ，此时

βα==N2ED(mN)=N∑Nn=1{tn−mTNϕ(xn)}2M2EW(mN)=MmTNmN