图像检索与降维(二):NetVLAD
论文地址:https://arxiv.org/abs/1511.07247
相比于大规模视觉场景识别方法,NetVLAD有以下几点优势:
1.提出了一种可训练的端到端的卷积神经网络框架直接用于场景识别任务,而其主要的成分则是NetVLAD层,是一种受VLAD(可看我的另一篇博客https://blog.csdn.net/LiGuang923/article/details/85416407)灵感激发的可泛化的VLAD层。
2.基于弱监督排序损失,提出了一种可训练的方法用于学习这种端到端框架的参数。
3.该方法的提升超越了当前最佳效果。
背景
场景识别问题存在极大的挑战,如何在不同的时间(白天or晚上)、不同的描述(照片中不同的角度)识别出一个城市或者一个国家中相同的街角?而最基础的一个问题则是,如何找到一个合适的图像描述方法以至于足够判断出那些看起来相似的场景。场景识别问题已经被传统的当作是一个实例检索任务,通过在一个大规模数据库中查询一个最相似的图片来完成一个图像定位的查询问题,图像数据库中的图像使用局部不变特征进行表示,例如SIFT、VLAD或者Fisher向量。在NetVLAD中,研究了这种图像表示方法在性能上的提升是否可以通过CNN来完成,这需要解决一下的问题:1.对于场景识别来说,什么样的CNN结构算是一个好的结构? 2.如何聚合足够数量的被标注数据用于训练网络? 3.如何为场景识别任务量身打造出一种可训练的端到端的网络结构?
针对第一个问题,提出了聚合中间层(conv5)的卷积特征(其信息量足够用于索引)用于场景识别的卷积神经网络结构,另外提出了一个可训练的NetVLAD层,该层可以应用到任何CNN结构中,并且可以通过后向传播进行训练,然后产生的图像聚合结构可以使用PCA压缩用于获得更为精简的图像表示。
针对于第二个问题,为了训练用于场景识别的框架,使用了Google Street View Time Machine上包括了不同视角和不同时间上的多全景大规模图像数据集,但是该数据集是一种弱监督形式的数据集:即两个在挨得很近的地点(基于给出的GPS信息)拍出的全景图可能拍摄的方向不同。
针对第三个问题,网络产生的图像表示对于视角和光线的改变是鲁棒的,同时学会专注于图像的相关部分,如建筑物外观和地平线,同时忽略可能出现在许多不同地方的混乱元素,如汽车和人。
解决第一个问题:NetVLAD
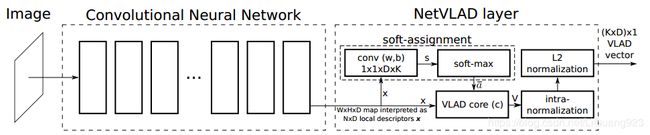
大多数图像索引流程是(1)提取局部特征 (2)将这些特征以一种无序的方式汇合。针对(1),在CNN的最后一层卷积层上裁剪(上图左边部分),并将其视为一个密度描述符提取器,实验证明,提取出的特征在实例检索和纹理识别上表现的比较好。另外,最后一层卷积层的输出是 H ∗ W ∗ D H*W*D H∗W∗D。针对(2),设计了一种新的池化层(上图右边部分),将被提取出来的描述符池化为一个固定的图像表示,并且其参数可通过后向传播进行学习,这种新的池化层被较为NetVLAD层。
NetVLAD层:原理与VLAD类似,给N个D维的局部图像描述符{ x i x_i xi}作为输入,以及K个聚类中心(“visual words”){ c i c_i ci}作为VLAD参数,VLAD图像表示V是一个 K ∗ D K*D K∗D维的向量,为了方便,将V当做是一个 K ∗ D K*D K∗D大小的矩阵,但是这个矩阵会被转化为一个向量,然后经过标准化,再被用于当做是图像表示。V的(j,k)元素可以由以下获得:
V ( j , k ) = ∑ a k ( x i ) ( x i ( j ) − c k ( j ) ) V(j,k) = \sum a_k(x_i) (x_i(j) - c_k(j)) V(j,k)=∑ak(xi)(xi(j)−ck(j))
其中 x i ( j ) x_i(j) xi(j)和 c k ( j ) c_k(j) ck(j)分别是第j个图像描述符和第k个聚类中心。 a k ( x i ) a_k(x_i) ak(xi)表示描述符 x i x_i xi到 c k c_k ck的关系,如果是1,则表示 c k c_k ck是距离 x i x_i xi最近的聚类中心,否则就是0。之后V会被转化为一个向量,然后再经过L2标准化。
为了构建出一个网络层可以通过后向传播被训练,需要该层的操作对应的参数以及输入是可微的,因此,这里的重点主要是使得VLAD池化可微,因为在VLAD中由于 a k ( x i ) a_k(x_i) ak(xi),函数是不连续的。为了使得池化可微,将上面的VLAD中 a k ( x i ) a_k(x_i) ak(xi)替换为了下式:
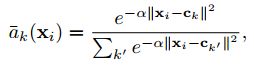
给 x i x_i xi到 c k c_k ck分配了权重作为他们的接近程度,其范围为0-1。 α \alpha α是一个正值常量,用于控制距离大小的衰减。当 α \alpha α趋向于正无穷时,上式就近似于之前的VLAD的 a k ( x i ) a_k(x_i) ak(xi)。另外,通过给该式一个平方,可以将 e − α ∣ ∣ x i ∣ ∣ 2 e^{-\alpha||x_i||^2} e−α∣∣xi∣∣2项取代为:

其中向量 w k = 2 α c k w_k = 2\alpha c_k wk=2αck,标量 b k = − α ∣ ∣ c k ∣ ∣ 2 b_k = -\alpha ||c_k||^2 bk=−α∣∣ck∣∣2。将该式加入VLAD中,得到NetVLAD的最终形式:
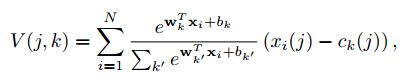
注意到第一项其实是一个soft-max函数 σ k ( z ) = e x p ( z k ) / ∑ e x p ( z k ) \sigma_k(z) = exp(z_k)/\sum exp(z_k) σk(z)=exp(zk)/∑exp(zk)。因此, x i x_i xi到 c k c_k ck的权重分配可以看做是包含两个步骤的过程:1.经过 w k w_k wk和 b k b_k bk的卷积,产生输出 s k ( x i ) = w k T x i + b k s_k(x_i) = w_k^Tx_i + b_k sk(xi)=wkTxi+bk。 2.卷积的输出经过一个softmax函数用于获取最终的权重分配 a k ( x i ) a_k(x_i) ak(xi)。最终得到的向量V经过标准化处理得到一个 ( K ∗ D ) ∗ 1 (K*D)*1 (K∗D)∗1的描述符。
解决二、三个问题
上面提到了存在两个问题:1.怎么聚合足够多的标注训练数据来训练网络 2.对于场景识别来说,一个合适的损失函数是什么? 为了解决这两个方法,首先将展示具有数量极大的Google Street View Time Machine弱标签全景图像集。另外,设计了一个新的弱监督排序损失用于处理数据集中不完整和具有噪声的位置信息标注。
数据集的弱监督性

像上图所示,相同的位置在不同的时间和季节中的照片给学习算法提供了重要信息用于发哪些特征是有用的或者是无用的。其中数据集中的每一个全景图片都伴随着一个GPS标签,可以被用于判别出那些在地理位置上接近的全景图片,但是并没有提供图片对应的是该位置的哪一部分场景,这就使得两个地理位置上接近的全景图像实际上式两个不同方向上拍摄的。在实验中,给定一个需要查询图像q,GPS信息只能用于分离1.正值{ p i q p_i^q piq},例如:与查询图像在地理位置上相近的图像集。 2.负值{ n j q n_j^q njq},例如:与查询图像相隔较远的图像集。
弱监督排序损失
我们希望学习到这样一个特征 f θ f_{\theta} fθ用以优化场景识别的性能。例如:给一个测试查询图像q,目标是将数据库图像从地理位置较近的 I i ∗ I_{i*} Ii∗到较远的 I i I_i Ii进行一个相似度排序,换句话说,我们希望查询图像q与其接近的图像 I i ∗ I_{i*} Ii∗的欧式距离 d θ ( q , I ) d_{\theta}(q,I) dθ(q,I)比q到较远的图像 I i I_{i} Ii要更小, d θ ( q , I i ∗ ) < d θ ( q , I i ) d_{\theta}(q,I_{i*}) < d_{\theta}(q,I_i) dθ(q,Ii∗)<dθ(q,Ii)。
定义一个元组: ( q , p i q , n j q ) (q,{p_i^q},{n_j^q}) (q,piq,njq),其中对于每个查询图像q,假设都有一个正值集{ p i q p_i^q piq}和一个负值集{ n j q n_j^q njq},而在正值集中至少有一个正值图像可以与查询图像匹配,但是我们不知道是哪一个图像。为了解决这种不确定性,提出了对最佳匹配的正值图像 p i ∗ q p_{i*}^q pi∗q的定义:
p i ∗ q = a r g m i n ( d θ ( q , p i q ) ) p_{i*}^q = argmin(d_{\theta}(q,p_i^q)) pi∗q=argmin(dθ(q,piq))
然后目标就变为学习到一个图像表示 f θ f_{\theta} fθ使得距离 d θ ( q , p i ∗ q ) d_{\theta}(q,p_{i*}^q) dθ(q,pi∗q)比q到负值集图像的距离 d θ ( q , n j q ) d_{\theta}(q,n_{j}^q) dθ(q,njq)更小:
d θ ( q , p i ∗ q ) < d θ ( q , n j q ) d_{\theta}(q,p_{i*}^q) < d_{\theta}(q,n_{j}^q) dθ(q,pi∗q)<dθ(q,njq)
基于这些,排序损失函数为:
L θ = ∑ l ( m i n ( d θ 2 ( q , p i q ) ) + m − d θ 2 ( q , n j q ) ) L_{\theta} = \sum l(min(d_{\theta}^2(q,p_{i}^q)) + m - d_{\theta}^2(q,n_{j}^q) ) Lθ=∑l(min(dθ2(q,piq))+m−dθ2(q,njq))
其中 l l l是一个转折函数 l ( x ) = m a x ( x , 0 ) l(x) = max(x,0) l(x)=max(x,0),m是一个常量用来作为边界。如果查询图像到负值集中的距离比边界加上查询图像到正值集中的距离还大,那么损失值为0。 f θ f_{\theta} fθ中的 θ \theta θ可以通过在一个大数据集上使用梯度下降训练获得。
参考
Relja A,Petr G,Akihiko T,et al. NetVLAD: CNN architecture for weakly supervised place recognition, 2016.