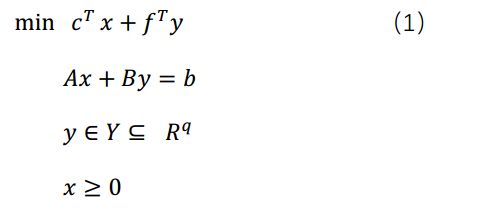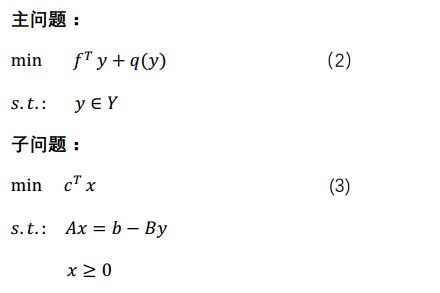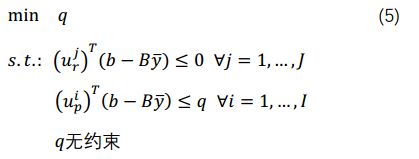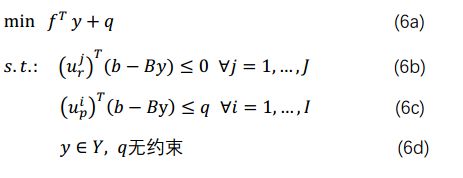运筹优化（十三）--大规模优化方法

针对因为算例的规模过大或者结果过于复杂而无法整体求解的数学模型，将原味分解成多个足够简单、可以单独迭代直接求解的子问题，伴随的主问题结合所有子问题的结果给出模型的精确或者近似精确的最优解，并将最优解相关的信息传递给子问题用以更新模型中相应的参数。

列生成算法

列生成算法通常被应用于求解大规模整数规划问题的分支定价算法(branch-and-price algorithm)中，其理论基础是由Danzig等于1960年提出。当求解一个最小化问题时，列生成算法主要的作用是为每个搜索树节点找到一个较优的下界(lower bound)。本质上而言，列生成算法就是单纯形法的一种形式，是用来求解线性规划问题的。列生成算法已被应用于求解如下著名的NP-hard优化问题：机组人员调度问题(Crew Assignment Problem)、切割问题(Cutting Stock Problem)、车辆路径问题(Vehicle Routing Problem)、单资源工厂选址问题(The single facility location problem )等。

列生成算法的基本思想

在某些线性优化问题的模型中,约束的数目有限，但是变量的数目随着问题规模的增长会爆炸式的增长，因此不能把所有的变量都显性的在模型中表达出来。在用单纯形法求解这类线性规划问题时，基变量(basic variable)只与约束的个数相关，每次迭代只会有一个新的非基变量(non-basic variable)进基，因此，在整个求解过程中其实只有很少一部分变量会被涉及到。简单来说，列生成算法通过求解子问题(pricing problem)，来找到可以进基的非基变量，该非基变量在模型中并没有显性的写出来（可以看成是生成了一个变量，每个变量其实等价于一列，所以该方法被称为列生成算法）。如果找不到一个可以进基的非基变量，那么就意味着所有的非基变量的检验数（reduced cost）都满足最优解的条件，也就是说，该线性规划的最优解已被找到，即使很多变量没有在模型中写出来。

拉格朗日松弛

拉格朗日松弛算法并不是采用直接搜索最优解的策略，而是希望通过对模型进行分解，计算模型最优目标函数值的较强的上下界。有时该分解算法可以用于求解大规模离散模型的线性松弛问题，另外有时，利用拉格朗日松弛甚至可以得到比线性松弛更好的上下界。该算法还可以提高分支界定或者分支割平面算法的求解效率，还可以结合取整运算为原模型得到近似最优解。

对于一个给定的整数规划问题，线性松弛是去掉模型中的整数约束，而拉格朗日松弛则是放松模型中的部分线性约束，保留整数约束和其他线性约束，这些被松弛的约束并不是完全去掉，而是在利用拉格朗日乘子在目标函数上增加相应的惩罚项，对不满足这些约束条件的解进行较大的惩罚。

考虑到任何一个合理的松弛问题都应该使得到的问题更加容易处理，因此，拉格朗日松弛通过利用对偶乘子尽可能松弛线性约束的方法，使得到的子问题更容易求解。

Dantzig-Wolfe分解

该分解算法不再是针对决策候选方案对应于完全信息下的列情况，而是借助拉格朗日松弛算法，将大量的 复杂约束与一个或多个具有容易处理的特殊结构（如网络流）的线性约束分解开。

DW分解的问题对应的约束条件具有如下的结构： 

第一行的约束Ay=b叫complicating/coupling constraints，后面的By=d可以看做是列生成的规则。 
DW分解的思路是，将变量用极点/极线表示。开始的时候极点/极线对应的变量很少，然后根据子问题的求解结果不断给主问题添加极点/极线。

3.1. 子问题

先给出Bx = b的一些极点和极线，比如说是 x1...xk  ，带入子问题求解： 
min Σi(cN−πAj)xi
s.t. Bixi=bi 
然后可以求得新的极点/极线 xk+1 

3.2. 限制主问题

min cy c y 
s.t. Ay=b（π）
y=Σux （这个约束可以用来消除模型中的 y  ） 
Σu=1（t）
t  是问题的上界，如果最优值 cy∗=t ，那么就取到了最优值，否则继续求解子问题添加变量。

benders 分解算法

Benders分解算法是由Jacques F. Benders在1962年首先提出，目的是用于解决混合整数规划问题(mixed integer programming problem,简称MIP问题)，即连续变量与整数变量同时出现的极值问题[1]。但它的实际应用并不限于此，A.M. Geoffrion建立了广义的Benders分解法，它可以对具有Benders分解基本形式的非线性问题求解，对子问题的求解方法也不必一定是线性的。Benders 分解法是一个很常用的方法，用来计算像整数非线性规划问题和随机规划问题之类的难以解决的问题。

Jacques F. Benders设计了一个巧妙的途径，来求解具有复杂变量的数学规划问题。所谓的复杂变量是指，当将这些变量固定后，剩下的优化问题（通常称为子问题）变得相对容易。在Benders考虑的一类特殊问题中，先把复杂变量的值固定，从而将问题规约为一个一般的线性规划问题，当然，这个线性规划问题是以复杂变量为参数的。在Benders设计的算法里，利用割平面的方式将主问题（以子问题的解为参变量）的极值和使子问题（线性规划问题）有可行解的参变量值的集合很恰当地表达了出来。过程中，对偶理论用来推导刻画这些表达式特征的自然割平面族，而带有参变量的线性规划问题被用来生成割平面。

在1976年，Florian[2]将这个算法应用于铁路机车的调度问题。1976年，Richardso[3]把这个算法应用于航空路线规划，1974年 Geoffrion和Graves[4]成功地把这个算法应用于设计工业分配系统。从1978年开始，Fisher和 Jaikumar[5]就在研究讨论利用这个算法的优势来规划机动车的路线。以上这些应用说明Benders分解算法用来解决各种特定结构的混合整规划问题有很大的优势。

2.Benders分解算法具体说明

给定一个线性优化问题：

其中x和y分别是p和q维向量，Y是y所在的可行域空间，A、B是矩阵，b、c、f表示适当的一维向量。

假设y是复杂变量，当y值固定时，原问题可以转化为相对容易求解的问题，利用Benders方法可以将问题分解为两部分：

其中q(y)表示当y值固定时子问题的最优解。

可以发现，子问题（3）是线性优化问题，如果子问题无界，那么主问题（2）也必定无界，此时原问题（1）也无界，那么原问题没有最优解。我们假设子问题（3）有界，我们可以通过求解子问题（3）的对偶问题来计算q(y)。子问题的对偶问题可以写成：

从对偶问题（4）中可以发现对偶问题的可行域不依赖于y的值，而y的值仅影响目标函数。因此，当我们给定y的值时，例如

,如果对偶问题的可行域为空，那么原问题无界或可行域也为空（此时对所有的y原问题都为空）。假设式子（4）不为空，我们可以枚举对偶问题所有的极点（extreme points）

和极射线(extreme rays)

，其中I和J分别表示极点和射线的个数。对于一个给定的y的值，

，可以通过检测：（a）对于所有的极射线式子

是否成立[6]，（b）能否找到一个极点使对偶问题目标函数值

最大。如果（a）存在，则对偶问题无界且原问题无解，如果（b）成立，则对偶问题和原问题都有有限的最优解。

注：（a）的理论依据见参考文献[2],178页Theorem 4.14，具体理论如下：

对于一个最小化问题

,约束条件为

,假设可行域中至少存在一个极点。则最优解为-∞的条件为当且仅当存在某个极射线d使

。注意本文中用来举例的子问题的对偶问题是最大化问题，参考文献[2]中提及的是最小化问题。

基于上述理论，对偶问题可以重新写成：

从（5）可以发现只有q一个变量，但是存在很多个约束。我们用（5）代替（2）中的q(y)，则原问题可以写成：

由于极射线和极点数量庞大，如果要生成所有的约束显然不现实。Benders算法求解的是松弛主问题（Relaxed master problem），即松弛主问题中的约束是原问题中约束（6b）和(6c）的一个子集。最开始，初始松弛主问题中无约束，在Benders算法求解过程中不断向松弛主问题中加入约束（6b）和(6c)中的某一个，即加入有效的切平面（cut）。通过求解松弛主问题，我们可以得到一个候选最优解(y*,q*)，然后将y*代入对偶子问题（4）中求解计算q(y*)值，如果子问题的最优解q(y*)=q*，则算法停止。如果对偶问题无解，则在松弛主问题中可以加入（6b）类型的约束，然后求解新的松弛主问题。（6b）类型的约束称之为Benders feasibility cuts。如果对偶子问题的最优解q(y*)>q*，则在松弛主问题中可以引入（6c）类型的约束，然后求解新的松弛主问题。（6c）类型的约束称之为Benders optimality cuts。在每次迭代过程中都可以生产某一类型的约束，由于I和J是有限的，故可以保证在有限次迭代过程后得到最优解。