【LCA】最近公共祖先问题Lowest Common Ancestors
昨天集训出了一道LCA的题目,我只会写暴力然后不知道为啥崩栈了,然后想起了去年NOIP Day1 T3 也是不会LCA就废了,然后就没有然后了.....于是我今天学习了各种LCA的做法。
LCA:对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。——百度百科
举个例子:
3和4节点的LCA就是2,2和6号节点的LCA是1,5和6的LCA就是5.
暴力求LCA的方法:
对树进行遍历求出每个节点的深度,如下图:
求任意两个节点的LCA,先把深度大的沿父亲移到同样的深度,若两个节点不是同一个结点就把两个结点同时向父亲移,最后结点相同得到的就是LCA。
举上图的例子,求3结点和5结点的LCA就,3结点深度大于5,先跳到2结点,两结点不同,继续跳,两节点都跳到1结点,1就是他们的LCA。
Code C++:
void dfs(int p,int dth){//对树进行遍历求深度
dep[p]=dth;
for(int i=first[p];i;i=e[i].next){
if(!dep[e[i].p]){
father[e[i].p]=p;
val[e[i].p]=e[i].l;
dfs(e[i].p,dth+1);
}
}
}
int lca(int x,int y){
while(dep[x]>dep[y])x=father[x];
while(dep[x]暴力 求一次LCA时间复杂度是O(树的深度)的,显然对于大数据会挂,那怎么办呢。
我们有LCA+RMQ(区间最值)的倍增在线算法
记得求区间最值的ST算法吗???
min[i][j]=min(min[i][j-1],min[i+(1<<(j-1))][j-1]);另fa[i][j]为i结点往上跳2^j的结点编号
易得fa[i][j]=fa[ fa[ i ][ j-1 ] ][ j-1 ](i结点往上跳2^(j-1)下再跳2^(j-1)就是i结点往上跳2^j的结果)
我们就能在O(nlogn)的时间预处理出这个东西
然后对每一个LCA的查询,还是先跳到相同深度,不过这次类似于二分查找地在logn的时间跳到相同深度结点,再把两个结点一起跳到使两个结点不同的最后两个结点,最终LCA就是fa[i][0].
时间复杂度:预处理O(nlogn)、一次查询(logn)
具体实现看下面代码。
我们先来看看2013Noip day1 T3 Trunk(Wikioi3282)
题目大意:给一个图,求最大生成树,询问生成树上两个结点路径上最小的边权,若两点不可达输出-1。
题解:先求最大生成树,然后对生成树dfs,并进行倍增同时记录g[i][j]表示以i为结点到i往上2^j个结点之间的最小边权,直接回答询问即可。
C++代码:
| 3287 货车运输NKWBTB | 测试通过 Accepted |
100
|
» | 561ms | 4296kb | C++ | 2068B |
#include
#include
#include
#include
#define MAXM 50001
#define MAXN 10001
#define DA 17
//DA开到2^n比N大就行
using namespace std;
int first[MAXN],father[MAXN],ct=1,fa[MAXN][DA],lth[MAXN][DA],dep[MAXN];
//father为并查集数组,fa是结点父亲倍增数组,lth为最小边权记录数组,dep为深度数组
struct edge{
int p,next,l;
void add(int u,int v,int val){
p=v;
next=first[u];
l=val;
}
}e[MAXM],line[MAXM*2];
bool cmp(const edge &a,const edge &b){return a.l>b.l;}
int findset(int x){
if(x!=father[x])father[x]=findset(father[x]);
return father[x];
}
bool Union(int x,int y){
int fx=findset(x);
int fy=findset(y);
if(fx==fy)return false;
father[fx]=fy;
return true;
}
void dfs(int p,int dth){
dep[p]=dth;
for(int i=first[p];i;i=e[i].next){
if(!fa[e[i].p][0]){
fa[e[i].p][0]=p;
lth[e[i].p][0]=e[i].l;
dfs(e[i].p,dth+1);
}
}
}
//对树进行遍历预处理出深度,初始化边权数组和倍增数组
int query(int u,int v){
int len=0x7fffffff;
if(dep[u]=0;i--)//将两结点跳到同样深度同时更新最小边权大小
if(dep[fa[u][i]]>=dep[v]){
len=min(len,lth[u][i]);
u=fa[u][i];
}
if(u!=v){//两节点同时跳到最后不同的两个结点
for(int j=DA-1;j>=0;j--)
if(fa[u][j]!=fa[v][j]){
len=min(len,min(lth[u][j],lth[v][j]));
u=fa[u][j];v=fa[v][j];
}
len=min(len,min(lth[u][0],lth[v][0]));
}
return len;
}
//查询
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i 如果查询不要求强制在线的话可以有离线的tarjan算法
时间复杂度为O(n+q)
参考文章:
http://en.wikipedia.org/wiki/Tarjan%27s_off-line_lowest_common_ancestors_algorithm
http://scturtle.is-programmer.com/posts/30055.html
这个算法思想大概是这样的
先把询问都存储下来
在遍历树的时候,维护一个并查集,当遍历原来树的一个子树的时候,把子树中的所有元素并为一个集合,把集合的根指向为子树的根,
那么我可以回答已经遍历过的点与子树跟的LCA询问,若询问点没有遍历过那么先放在一边不管。
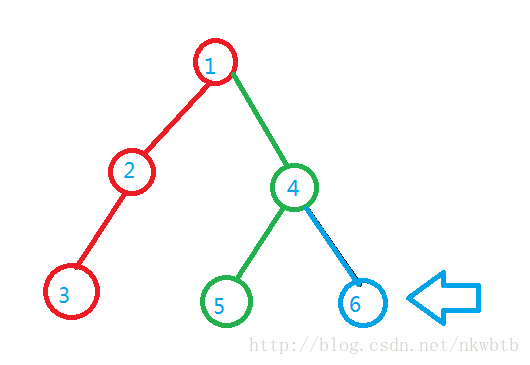
例:
箭头表示当前遍历到的结点,相同颜色的点表示已经并入同一集合,如题,现在遍历到点6,回答与结点6有关的询问,假若询问3和6号点的LCA 先检查3号点是否遍历过,然后答案为3所在并查集的祖先,也就是1号点。
又来一题:
WIKIOI 1036
题目大意:给一棵树,给定结点顺序,求从根节点按结点顺序走的最终距离是多少,其中每条边的长度都是1.
解法:显然求相邻点的LCA,然后他们之间的距离就是i到根的距离+j到根的距离-2*LCA到根的距离,累加得到答案即可。
代码:
| 1036 商务旅行NKWBTB | 测试通过 Accepted |
100
|
» | 55ms | 3008kb | C++ | 1252B |
#include
#include
#include
#include
#include
#define MAXN 30001
using namespace std;
int first[MAXN],fa[MAXN],ct=1,anc[MAXN],lth[MAXN],ans=0;
bool vis[MAXN];
struct edge{
int p,next;
void add(int u,int v){
p=v;
next=first[u];
}
}e[MAXN*2];
vectorvec[MAXN];
vector::iterator it;
int findset(int x){
if(x!=fa[x])fa[x]=findset(fa[x]);
return fa[x];
}
bool Union(int x,int y){
int fx=findset(x);
int fy=findset(y);
if(fx==fy)return false;
fa[fx]=fy;
return true;
}
void tarjan(int p,int f,int l){
fa[p]=p;lth[p]=l;//处理距离
for(int i=first[p];i;i=e[i].next){
if(!fa[e[i].p]&&e[i].p!=f){
tarjan(e[i].p,p,l+1);
Union(p,e[i].p);//合并子树结点到并查集中
anc[findset(p)]=p;//并查集根指向子树根节点
}
}
vis[p]=true;
for(it=vec[p].begin();it!=vec[p].end();it++){//回答与p相关询问
if(vis[*it])ans+=lth[p]+lth[*it]-2*lth[anc[findset(*it)]];
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i ————————————————————————————————————————————————
P.S.:以前XTC大神讲过noip 2013 day1 t3 可以tarjan做,可是我想了很久还是不会。。。。。。求大神指点