2018 多校第五场部分题解
链接:2018 Multi-University Training Contest 5
过题数:1
排名:470/704
B. Beautiful Now
题意
给定一个没有前导零的整数 n n ,其十进制表示为 (x1x2⋯xm)10 ( x 1 x 2 ⋯ x m ) 10 ,即 n=∑mi=110m−ixi n = ∑ i = 1 m 10 m − i x i ,可以对这个整数进行 k k 次操作,每次操作选择两个整数 i,j (1≤i≤j≤m,xj≠0) i , j ( 1 ≤ i ≤ j ≤ m , x j ≠ 0 ) 并将这两个位置上的数字交换,问最终能够交换得到的最小的数字和最大的数字分别是多少。
输入
第一行为一个整数 T (1≤T≤100) T ( 1 ≤ T ≤ 100 ) ,接下去 T T 行每行两个整数 n,k (1≤n,k≤109) n , k ( 1 ≤ n , k ≤ 10 9 ) 。
输出
每组数据输出经过 k k 次合法交换后能够得到的最大值和最小值。
样例
| 输入 |
|---|
| 5 12 1 213 2 998244353 1 998244353 2 998244353 3 |
| 输出 |
| 12 21 123 321 298944353 998544323 238944359 998544332 233944859 998544332 |
题解
由于每次交换可以选择 1≤i≤j≤m 1 ≤ i ≤ j ≤ m ,其中 i i 可以等于 j j ,因此答案可以从任意小于等于 k k 次的合法交换中取最小值得到,题目要求在交换过程中不允许出现前导零,可以证明,如果交换的结果不含有前导零,就一定存在一种方式在不出现前导零的情况下从原数字得到结果数字。最后就是暴力枚举所有交换次数小于等于 k k 的全排列,每次 O(n) O ( n ) 生成全排列会超时,可以预处理 9 9 以内的全排列(如果长度达到 10 10 就只有一种答案),全排列的交换次数可以用并查集找环计算。如果 k k 大于等于 m−1 m − 1 直接生成不含前导零的最小字典序和最大字典序作为答案。
过题代码
#include
#include E. Everything Has Changed
题意
在平面直角坐标系内有一个圆心在原点,半径为 R R 的初始圆,以及 m m 个圆心在 (xi,yi) ( x i , y i ) ,半径为 ri r i 的圆,这 m m 个圆两两互不相交且不会包含整个初始圆,这 m m 个小圆将对初始圆进行切割,问最终初始圆的周长。
输入
第一行为一个整数 T (1≤T≤1000) T ( 1 ≤ T ≤ 1000 ) ,接下去有 T T 组数据,每组数据第一行为两个整数 m,R (1≤m≤100) m , R ( 1 ≤ m ≤ 100 ) ,接下去 m m 行每行三个整数 xi,yi,ri (−1000≤xi,yi≤1000,1≤R,ri≤1000) x i , y i , r i ( − 1000 ≤ x i , y i ≤ 1000 , 1 ≤ R , r i ≤ 1000 ) 。
输出
输出最终圆的周长,误差在 10−6 10 − 6 以内都认为答案正确。
样例
| 输入 |
|---|
| 1 4 10 6 3 5 10 -4 3 -2 -4 4 0 9 1 |
| 输出 |
| 81.62198908430238475376 |
| 提示 |
切割圆的方式如下: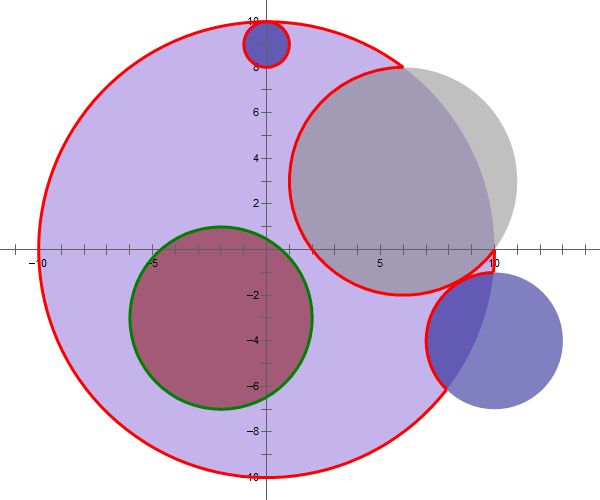 其中红线为圆的周长。 |
题解
对于两圆相离或者外切的情况,对周长的贡献都为 0 0 ,对于两圆内含的情况,贡献也为零,因此只要考虑两圆相交与内切的情况,先考虑第一种相交(两圆圆心在交点连线的两侧):
设 AG=h,O1O2=d,O1G=a,O2G=b A G = h , O 1 O 2 = d , O 1 G = a , O 2 G = b ,则可以联立方程:
⎧⎩⎨⎪⎪a2+h2=r21b2+h2=r22a+b=d { a 2 + h 2 = r 1 2 b 2 + h 2 = r 2 2 a + b = d解方程得到 b=r22−r21+d22d b = r 2 2 − r 1 2 + d 2 2 d ,而对于两圆圆心在交点连线同侧的情况:
只需要将上面方程组的第 3 3 个方程改为 a−b=d a − b = d 即可,得到 b=−r22−r21+d22d b = − r 2 2 − r 1 2 + d 2 2 d ,发现和上式差一个负号,要求圆 O2 O 2 的贡献,就是求圆 O2 O 2 在圆 O1 O 1 内部的圆弧长度,因此如果直接对 br2 b r 2 取 arccos arccos ,第二种情况的负号正好使得圆 O2 O 2 的圆心角计算得到大于 90° 90 ° 的部分。
最后还需要减掉圆 O1 O 1 在圆 O2 O 2 内部的圆弧长度,计算方式与第一种情况相同。
过题代码
#include
#include G. Glad You Came
题意
有一个长度为 n n 的序列,序列中每个数字的初始值都为 0 0 ,接下来对这个序列进行 m m 次操作,每次操作将区间 [li,ri] [ l i , r i ] 之间的所有数字 ai a i ,都更新为 max(ai,vi) max ( a i , v i ) ,输出 m m 次操作后 ⨁ni−1i×ai ⨁ i − 1 n i × a i 的值。为了避免大数据输入,给出初始随机种子 X,Y,Z X , Y , Z ,每次随机数字由以下伪代码生成:
总共生成 3m 3 m 个随机数 f1,f2,⋯,f3m f 1 , f 2 , ⋯ , f 3 m ,第 i i 次操作的 li,ri,vi l i , r i , v i 由以下规则得到:
lirivi=min((f3i−2%n)+1,(f3i−1%n)+1)=max((f3i−2%n)+1,(f3i−1%n)+1)=f3i%230(1)(2)(3) (1) l i = min ( ( f 3 i − 2 % n ) + 1 , ( f 3 i − 1 % n ) + 1 ) (2) r i = max ( ( f 3 i − 2 % n ) + 1 , ( f 3 i − 1 % n ) + 1 ) (3) v i = f 3 i % 2 30
输入
第一行为一个整数 T (1≤T≤100) T ( 1 ≤ T ≤ 100 ) ,接下去 T T 行每行 5 5 个整数 n,m,X,Y,Z (1≤n≤105,1≤m≤5×106,0≤X,Y,Z<230) n , m , X , Y , Z ( 1 ≤ n ≤ 10 5 , 1 ≤ m ≤ 5 × 10 6 , 0 ≤ X , Y , Z < 2 30 ) 。
输出
对于每组数据,输出最终结果。
样例
| 输入 |
|---|
| 4 1 10 100 1000 10000 10 100 1000 10000 100000 100 1000 10000 100000 1000000 1000 10000 100000 1000000 10000000 |
| 输出 |
| 1031463378 1446334207 351511856 47320301347 |
| 提示 |
| 第一组数据经过 10 10 次操作序列元素为 [1031463378] [ 1031463378 ] ; 第二组数据经过 100 100 次操作后数组元素为 [1036205629,1064909195,1044643689,1062944339,1062944339,1062944339,1062944339,1057472915,1057472915,1030626924] [ 1036205629 , 1064909195 , 1044643689 , 1062944339 , 1062944339 , 1062944339 , 1062944339 , 1057472915 , 1057472915 , 1030626924 ] 。 |
题解
反向用 ST S T 表 O(1) O ( 1 ) 地标记最大值更新,最后从大到小将最大值标记往下打,就可以得到答案,时间复杂度为 O(m+nlogn) O ( m + n log n ) 。
过题代码
#include
#include H. Hills And Valleys
题意
给定一个长度为 n n 的序列,可以选择序列上的一个区间 [l,r] (1≤l≤r≤n) [ l , r ] ( 1 ≤ l ≤ r ≤ n ) ,将这个区间上的所有数字翻转,求进行一次操作后能够得到最长非递减子序列的长度。
输入
第一行为一个整数 T (1≤T≤100) T ( 1 ≤ T ≤ 100 ) ,接下去有 T T 组数据,每组数据第一行为一个整数 n (1≤n≤105) n ( 1 ≤ n ≤ 10 5 ) ,第二行包含一个长度为 n n 的数字字符串 A1A2⋯An (0≤Ai≤9) A 1 A 2 ⋯ A n ( 0 ≤ A i ≤ 9 ) 。
输出
输出经过一次交换后能够得到的最长非递减子序列的长度,以及翻转区间的左右端点。
样例
| 输入 |
|---|
| 2 9 864852302 9 203258468 |
| 输出 |
| 5 1 8 6 1 2 |
| 提示 |
| 第一组数据将 864852302 864852302 区间 [1,8] [ 1 , 8 ] 内的数字翻转后结果为 032584682 032584682 ,其最长非递减子序列长度 03588 03588 ; 第二组数据将 203258468 203258468 区间 [1,2] [ 1 , 2 ] 内的数字翻转后结果为 023258468 023258468 ,其最长非递减子序列长度 023588 023588 。 |
题解
假设将最长非递减子序列中的每段连续相同数字都缩成一个数字,如: 0123456789 0123456789 ,则问题可以转化为求原序列与这个序列的最长“公共”子序列,这个序列中的每个数字可以匹配零次或多次,这个问题可以用 dp d p 来解决,状态定义为 dp[i][j] d p [ i ] [ j ] ,表示第一个序列前 i i 位与第二个序列前 j j 位的最大匹配长度,时间复杂度为 O(nm) O ( n m ) , m m 为第二个序列的长度。
如果原序列翻转最长非递减子序列的区间为 [l,r] [ l , r ] ,则第二个序列应构造为 012⋯(l−1)lr(r−1)(r−2)⋯(l+1)lr(r+1)⋯89 012 ⋯ ( l − 1 ) l r ( r − 1 ) ( r − 2 ) ⋯ ( l + 1 ) l r ( r + 1 ) ⋯ 89 ,如翻转区间为 [3,7] [ 3 , 7 ] ,就要构造 012376543789 0123 76543 789 ,再与第一个序列进行最长“公共”子序列匹配, 7 7 之前的 3 3 是因为如果翻转的子序列区间为 [3,7] [ 3 , 7 ] ,那么在第一个 7 7 之前的那部分 3 3 在翻转后也对最长非递减子序列有贡献,如果直接忽略这个 3 3 ,那部分贡献就没有算上去,会导致漏算。
最后输出翻转的区间,只要将翻转区间跟着 dp d p 一起更新即可,用 dpl d p l 和 dpr d p r 表示 dp d p 取得最大值时翻转的区间,其中 dpl d p l 在多个 dp d p 取最大值时应取最靠前的位置, dpr d p r 只要跟着更新,就可以得到最后一个翻转的位置。
过题代码
#include
#include 