机器学习： 提升

Github

系列文章 pdf 版本已经上传至： https://github.com/anlongstory/awsome-ML-DL-leaning/tree/master/xiaoxiang-notes
欢迎 Star 和下载

提升的概念理解

这部分是紧紧衔接《机器学习： 决策树与随机森林》 部分内容的。首先说明一个它们与随机森林方法的区别

与随机森林的比较

• 随机森林是随机选择 k 个特征去构建 CART 树，重复 m 次，得到的 m 个决策树的最终结果求平均得到最后的结果。这些模型之间相互是独立产生的，只是最后投票的时候将它们结果联系在一起。
• 提升的方法思想是每一步产生一个弱预测模型（如决策树），并加权累加到总模型中。现在第 n 项的模型预测都是依赖前面 n-1 项的结果得到的，依据的是损失函数的梯度方向，所以称之为梯度提升（Gradient Boosting）

提升算法

梯度提升算法首先给定一个目标损失函数，它的定义域是所有可行的弱函数集合（基函数），提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值。
上面这段话转化成机器学习中的概念和数学表达就是：
首先要给定一个目标损失函数:
目标函数是从我们的数据中得到的，我们表示输入数据为：$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$,其中 $x_i$ 表示输入向量，$y_i$ 代表对应的标签，目标是找到一个近似函数 $\hat{F}(x)$ 使得损失函数 $L\left(y,F(x)\right)$ 的损失值最小，这里的损失函数典型的就是：
$$L\left(y,F(x)\right)=\frac{1}{2}{\left(y-F(x)\right)}^2$$$$L\left(y,F(x)\right)=\left|y-F(x)\right|$$
现在可以假设我们的 $F(x)$ 是一族基函数$f_i(x)$ 的加权和：
$$F\left(x\right)=\sum _{i=1}^M{\gamma }_i{f}_i(x)+const$$

(1)

我们以贪心的思路来扩展 $F(x)$ 中的基函数，但是每次要选择最优的基函数还是很困难，所以这里任然使用 梯度下降 算法近似计算。
将所给样本代入基函数 $f(x)$ 得到 $f(x_1),f(x_2),...,f(x_n)$, 从而可以得到关于目标函数 $L$的向量，为 $L(y_1,f(x_1)),L(y_2,f(x_2)),...,L(y_n,f(x_n))$，我们对这个向量对于 $f$ 求偏导，让它们沿着 负梯度方向下降一点点：
$$F_m(x)=F_{m-1}(x)-{\gamma }_m\sum _{i=1}^n{▽}_{f}L(y_i,F_{m-1}(x))$$

(2)

这里的 ${\gamma }_m$ 就是步长，可以使用线性搜索求最优步长。
$${\gamma }_m=\underset{\gamma }{\mathrm{argmin}}\sum _{i=1}^{n}L(y_i,F_m(x))$$

(3)

综上所述：

• 我们可以先给定一个初始基函数 $F_0(x)=\underset{\gamma }{\mathrm{argmin}}{\sum }_{i=1}^{n}L(y_i,\gamma )$，然后通过求偏导计算为伪残差 :$$r_{im}={\left[\frac{\partial L(y_i,F(x))}{\partial F(x)}\right]}_{F(x)=F_{m-1}(x)}$$
• 使用数据 $(x_i,r_{im})$ 计算拟合残差的基函数 $f_m(x)$
• 使用公式（3）计算步长 $r_m$
• 更新模型$F_m(x)=F_{m-1}(x)-{\gamma }_m{f}_m(x_i)$

GBDT

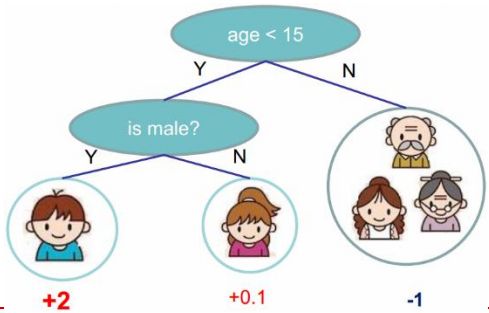
梯度提升树（GBDT）的基函数就是决策树（CART 树），第 m 步的梯度提升是根据伪残差数据计算第 m 棵决策树 $t_m(x)$ 的。这里我们可以令树 $t_m(x)$ 的叶节点数目为 $J$，这样决策树就将输出空间划分成了 $J$ 个不相交的区域 $R_{1m},R_{2m},...,R_{jm}$，并且决策树可以在每个区域中给出某个类型的确定性预测。

以上面图为例，这里 $J=3$，对应的确定性预测值就是下面的 +2，+0.1，-1，所以对于决策树，对于输入 $x$ ，决策树可以表示为：
$$t_m(x)=\sum _{j=1}^J{b}_{jm}I(x\in R_{jm})$$

(4)

其中 $b_{jm}$ 是样本 $x$ 在区域 $R_{jm}$ 的预测值。
所以根据上面的分析，这里直接可以将基函数表示成公式（4）的形式，代入公式（3）可得：
$${\gamma }_m=\underset{\gamma }{\mathrm{argmin}}\sum _{i=1}^{n}L(y_i,F_{m-1}(x)+\gamma t_m(x))$$

(5)

对树的每个区域分别采用线性搜索计算步长，从而系数 $b_{jm}$ 被合并到步长中。

参数设置和正则化

对训练集过度拟合会降低模型的泛化能力，所以训练过程中需要加入一些正则化技术来降低过拟合：

• 复杂度使用叶节点个数或者叶节点预测值的平方（一般叶节点树为 4-8 之间）
• 决策树剪枝 （包括对包含最少样本数目做限制）
• 梯度提升的迭代次数也要注意

当损失函数是最小平方误差、绝对值误差时 GBDT 解决的是回归问题，当损失函似是多类别的 Logistic 似然函数则是分类问题。

XGBoost

前面提到，一颗决策树的核心就是树结构和叶权值。XGBoost 主要就是采用泰勒展开式：
$$f(x+△x)\approx f(x)+f^{\prime }(x)△x+\frac{1}{2}{f}^{\prime \prime }(x)△x^2$$

(6)

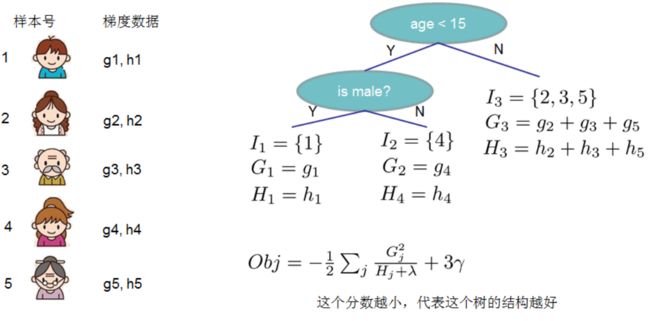
将二阶导数信息加入考虑范围，这里用 $g_i$ 表示一阶导数， $h_i$ 表示二阶导数，定义：
$$G_j=\sum _{i\in I_j}{g}_i，H_j=\sum _{i\in I_j}{h}_i$$

(7)

最终经过复杂的推导，这里使目标函数对预测权值求偏导可以得到：
$$w_j=-\frac{G_j}{H_j+\lambda }$$
代回目标函数可以得到：
$$J(f_t)=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

(8)

这里的 $T$ 表示叶节点的个数。以下面的图来做一个举例，假设有 5 个样本，它们对应的一阶，二阶梯度信息就是 $g_j,h_j$，这样的决策树

对于当前节点，我们可以计算所有可行的划分后的 $J(f_t)$ ，然后选择所有可行划分中 $J(f_t)$ 最小的分割点，换而言之，我们枚举可行的分割点，选择增益最大的划分，继续同样的操作，直到满足某阈值或得到纯节点，这里计算收益的公式可以表示为：
$$Gain(\varphi )=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$

(9)

这里的下标 $G_L$, $G_R$ 分别表示当选择一个分割点时，被划分到对应左右两边区域的一阶梯度总合。

所以综上所述：
相较于 GBDT ，XGBoost 使用可二阶导数信息，可以更快的在训练集上收敛，也属于随即森林类的方法，本身比较容易过拟合，因为实现过程中使用了并行/多核运算，所以它的速度比较快。

Adaboost

前面介绍的两个 GBDT， XGBoost 都是通过前面的模型来推断出下一个模型，这一小节要介绍的 Adaboost （自适应性提升方法）则是对训练数据集每个样本赋予一个权值，然后在每次迭代的过程中对这个权值分布进行不断调整，包括计算出每个模型的权值系数，最后叠加，由多个弱分类器叠加成一个强分类器。
首先划分问题的每个基本分类器看作是一个二分类问题：$G_m(x):\chi \in \left\{-1,+1\right\}$
基本分类器的分类误差可以表示为：$e_m={\sum }_{i=1}^N{w}_{mi}I(G_m(x_i)̸=y_i)$
通过上面的误差率计算出当前基本分类器的系数为：$${\alpha }_m=\frac{1}{2}log\frac{1-e_m}{e_m}$$

(10)

根据上面的分类器系数来更新训练数据集的权值分布,式中的 $Z_m$ 主要是为了归一化操作，使所有权值成一个概率分布：
$$w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i)),其中Z_m=\sum _{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))$$

(11)

最后构建的分类器就是所有基本分类器的线性组合：
$$f(x)=\sum _{m=1}^M{\alpha }_m{G}_m(x)$$

(12)

这里以李航博士《统计学习方法》中的例子说明上述算法。
首先假设我们有 10 个数据点，对应编号 X 为 0-9，它们对应的标签为 $\{-1,+1\}$

X	0	1	2	3	4	5	6	7	8	9
Y	1	1	1	-1	-1	-1	1	1	1	-1
W	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1

刚开始我们都是假设权值均匀分布（认为重要性相同），所以均值都为 $\frac{1}{N}$, $N$ 为样本个数。经过计算我们的阈值设为 2.5 的时候基本分类器的分类误差率使最低的，所以第一个分类器为：
$$G_1(x)=\{\begin{array}{c}1,x<2.5\\ -1,x>2.5\end{array}$$
这时候的误差率为 $e_1=0.3$ （刚开始权值相同，阈值 2.5 的时候，10个里面分类错了 3 个，所以为 0.3），计算出 $G_1$ 的系数：
$${\alpha }_1=\frac{1}{2}log\frac{1-e_1}{e_1}=0.4236$$
所以当前分类器为 $f_1(x)=0.4236\ast G_1(x)$,分类器 $sign(f_1(x))$ 在训练集上有 3 个误分类点。
对于上面的结果使用公式（11）进行计算，得到新的权值分布为:

X	0	1	2	3	4	5	6	7	8	9
Y	1	1	1	-1	-1	-1	1	1	1	-1
W	0.0715	0.0715	0.0715	0.0715	0.0715	0.0715	0.1666	0.1666	0.1666	0.0715

可以看到刚才分错的 3 个样本的权值比其他正确分类的都要大了，模型会放更多的精力在这些分错的例子上。
通过比较不同的阈值得到在这个分布上，阈值取 8.5 时误差率最低，这时基本分类器为:
$$G_2(x)=\{\begin{array}{c}1,x<8.5\\ -1,x>8.5\end{array}$$
这时候的误差率为 $e_2=0.2143$ （这时候分错的是 x<8.5 左边的 3 个标签为 -1 的样本，所以为 0.0715*3）
$${\alpha }_2=\frac{1}{2}log\frac{1-e_2}{e_2}=0.6496$$
所以当前分类器为$f_2(x)=0.4236\ast G_1(x)+0.6496\ast G_2(x)$, 分类器 $sign(f_2(x))$ 在训练数据集上有 3 个误分类点。
对于上面的结果使用公式（11）进行计算，得到新的权值分布为:

X	0	1	2	3	4	5	6	7	8	9
Y	1	1	1	-1	-1	-1	1	1	1	-1
W	0.0455	0.0455	0.0455	0.1667	0.1667	0.1667	0.1060	0.1060	0.1060	0.0455

通过比较不同的阈值得到在这个分布上，阈值取 5.5 时误差率最低，这时基本分类器为:
$$G_3(x)=\{\begin{array}{c}1,x>5.5\\ -1,x<5.5\end{array}$$
这时候的误差率为 $e_3=0.1820(0.0455\ast 4)$
$${\alpha }_3=\frac{1}{2}log\frac{1-e_3}{e_3}=0.7514$$
所以当前分类器为$f_3(x)=0.4236\ast G_1(x)+0.6496\ast G_2(x)+0.7514\ast G_3(x)$,分类器 $sign(f_3(x))$ 在训练数据集上有 0 个误分类点。

还可以根据当前的模型系数，继续更新权值分布，只是本题到这里已经满足需求了。

算法总结

上面通过对实例讲解介绍了 Adaboost 的基本步骤和计算方法，其中直接给出的权重计算公式（10）和权重调整公式（11）背后都是有前向分布算法包括一些复杂的数学推导的，这里能力有限，就不展开介绍，有兴趣的读者可以自行查找对应资料。

Adaboost 算法是模型为加法模型、损失函数为指数函数、每一个基函数的学习算法为前向分布算法时的二类学习方法。，其训练误差是以指数速率下降的，因为它不需要事先知道下届 $\gamma$，具有自适应性（Adaptive）。

Bagging 能够减少训练方差(Variance)，对于不剪枝的决策树、神经网络等学习器有良好的集成效果。Boosting 减少偏差（Bias）,能够基于泛化能力较弱的学习器构造强学习器。