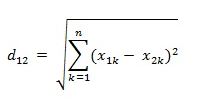【算法】距离算法总结

1.   欧氏距离

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义

在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。

在二维和三维空间中的欧氏距离就是两点之间的实际距离。

 

二维公式：

 

三维公式：

 

n维公式：

或

 

向量运算表现形式：

 

python实现：

"""欧氏距离"""
import numpy as np
from scipy.spatial.distance import pdist

# 向量
# 二维
# A = np.array([1,2])
# B = np.array([1,3])

# n维
A = np.random.random (10) #10维
B = np.random.random (10)

print("向量：",A,B)

#矩阵
# A = np.mat([1,2])
# B = np.mat([1,3])


# 公式求解
d1 = np.sqrt(np.sum(np.square(A-B)))
print("结果:",d1)

# scipy库求解
X = np.vstack([A,B])
d2 = pdist(X)
print("结果:",d2)

2.   标准化欧氏距离

标准欧氏距离(Standardized Euclidean distance )的定义
　　标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路：既然数据各维分量的分布不一样，好吧！那我先将各个分量都“标准化”到均值、方差相等吧。均值和方差标准化到多少呢？这里先复习点统计学知识吧，假设样本集X的均值(mean)为m，标准差(standard deviation)为s，那么X的“标准化变量”表示为：

　　标准化后的值 =  ( 标准化前的值  － 分量的均值 ) /分量的标准差
　　经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式：

　　如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。

 

 

python实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

X=np.vstack([x,y])

#方法一：根据公式求解
sk=np.var(X,axis=0,ddof=1)
d1=np.sqrt(((x - y) ** 2 /sk).sum())
print(d1)

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
d2=pdist(X,'seuclidean')
print(d2)

3.   马氏距离

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示数据的协方差距离。

一种有效的计算两个未知样本集的相似度的方法。

与欧氏距离不同的是它考虑到各种特性之间的联系并且是尺度无关的(scale-invariant)，即独立于测量尺度。

 

有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：

 

而其中向量Xi与Xj之间的马氏距离定义为：

 

 若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：

 

假设ux为向量X={x1,x2,...,xN}X={x1,x2,...,xN}的均值，uy为Y={y1,y2,...yN}Y={y1,y2,...yN}的均值，ΣΣ 是协方差矩阵，点X与Y的马氏距离：

 

若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。

 

其中Σ是X与Y的协方差矩阵 
可见： 
如果Σ是单位矩阵，则马氏距离退化成欧式距离； 
如果Σ是对角矩阵，则称为归一化后的欧式距离。 

 

马氏距离的特点：

• 尺度无关
• 考虑进数据之间的联系

马氏距离可以通过协方差自动生成相应的权重，而使用逆则抵消掉这些权重。

 

 

python实现：

"""马氏距离"""
import numpy as np
from scipy.spatial.distance import pdist

A=np.random.random(10)
B=np.random.random(10)


#马氏距离要求样本数要大于维数，否则无法求协方差矩阵
#此处进行转置，表示10个样本，每个样本2维
X=np.vstack([A,B])
XT=X.T

# 方法一：根据公式求解
S = np.cov (X)  # 两个维度之间协方差矩阵
SI = np.linalg.inv (S)  # 协方差矩阵的逆矩阵
# 马氏距离计算两个样本之间的距离，此处共有10个样本，两两组合，共有45个距离。
n = XT.shape[0]
d1 = []
for i in range (0, n):
    for j in range (i + 1, n):
        delta = XT[i] - XT[j]
        d = np.sqrt (np.dot (np.dot (delta, SI), delta.T))
        d1.append (d)
print(d1)

# 方法二：根据scipy库求解
d2 = pdist (XT, 'mahalanobis')
print(d2)

马氏优缺点：

1）马氏距离的计算是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

2）在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

3）还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点（3，4），（5，6）和（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

4）在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的，而所有样本点出现3）中所描述的情况是很少出现的，所以在绝大多数情况下，马氏距离是可以顺利计算的，但是马氏距离的计算是不稳定的，不稳定的来源是协方差矩阵，这也是马氏距离与欧式距离的最大差异之处。

 

优点：

它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。缺点：它的缺点是夸大了变化微小的变量的作用。

4.   曼哈顿距离

出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 

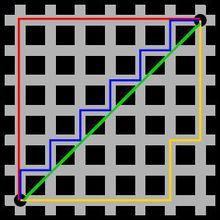
使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

 

图中红线代表曼哈顿距离，绿色代表欧氏距离，蓝色和黄色代表等价的曼哈顿距离。

 

(1)  二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离

(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离
或

p是I的维度。当I为图像坐标时，曼哈顿距离即是x,y坐标距离之和。

 

 

Python实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#方法一：根据公式求解
d1=np.sum(np.abs(x-y))
print(d1)

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
X=np.vstack([x,y])
d2=pdist(X,'cityblock')
print(d2)

5.   切比雪夫距离

切比雪夫距离( Chebyshev Distance )或是L∞度量是向量空间中的一种度量

二个点之间的距离定义是其各坐标数值差绝对值的最大值。

以数学的观点来看，切比雪夫距离是由一致范数所衍生的度量，也是超凸度量的一种

以任一点为准，和此点切比雪夫距离为r的点会形成一个正方形，其边长为2r，且各边都和坐标轴平行。

 

(1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离

(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离

　　这个公式的另一种等价形式是

       看不出两个公式是等价的？提示一下：试试用放缩法和夹逼法则来证明。

 

在python中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#方法一：根据公式求解
d1=np.max(np.abs(x-y))
print(d1)

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
X=np.vstack([x,y])
d2=pdist(X,'chebyshev')
print(d2)

6.   闵可夫斯基距离

闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。

闵可夫斯基距离^[2]  ,是欧氏空间中的一种测度，被看做是欧氏距离的一种推广，欧氏距离是闵可夫斯基距离的一种特殊情况。

 

定义式：ρ(A，B) = [ ∑( a[i] - b[i] )^p ]^(1/p) (i = 1，2，…，n)

闵可夫斯基距离公式中，当p=2时，即为欧氏距离；当p=1时，即为曼哈顿距离；当p→∞时，即为切比雪夫距离。

 

绝对值距离和欧几里德距离都称为闵可夫斯基（Minkowski）距离（以下简称闵氏距离）

（1）闵氏距离与特征参数的量纲有关，有不同量纲的特征参数的闵氏距离常常是无意义的。

（2）闵氏距离没有考虑特征参数间的相关性，而马哈拉诺比斯距离解决了这个问题。

 

闵氏距离不是一种距离，而是一组距离的定义。

 

闵式距离公式：Dm(v1,v2)= [∑(ωi-ωj) ]

闵氏距离法(D=4)

 

(1) 闵氏距离的定义
       两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

也可写成

其中p是一个变参数。
当p=1时，就是曼哈顿距离
当p=2时，就是欧氏距离
当p→∞时，就是切比雪夫距离
       根据变参数的不同，闵氏距离可以表示一类的距离。

 

闵氏距离的缺点主要有两个：

(1)将各个分量的量纲(scale)，也就是“单位”当作相同的看待了。

(2)没有考虑各个分量的分布（期望，方差等)可能是不同的。

 

python实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#方法一：根据公式求解,p=2
d1=np.sqrt(np.sum(np.square(x-y)))
print(d1)

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
X=np.vstack([x,y])
d2=pdist(X,'minkowski',p=2)
print(d2)

7.   海明距离

在信息编码中，两个合法代码对应位上编码不同的位数称为码距，又称海明距离(Hamming distance)。

两个码字的对应比特取值不同的比特数称为这两个码字的海明距离。

在一个有效编码集中,任意两个码字的海明距离的最小值称为该编码集的海明距离。

汉明距离是两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。

汉明重量是字符串相对于同样长度的零字符串的汉明距离

 

python实现：

def hamming_distance(s1, s2):
    assert len(s1) == len(s2)
    return sum(ch1 != ch2 for ch1, ch2 in zip(s1, s2))

print (hamming_distance("gdad","glas"))

8.   余弦距离

余弦相似度（Cosine  distance）用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。

相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。

余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

 

公式如下：

 

Python实现：

import numpy as np
from scipy.spatial.distance import pdist

x = np.random.random (10)
y = np.random.random (10)

# solution1
dist1 = 1 - np.dot (x, y) / (np.linalg.norm (x) * np.linalg.norm (y))

# solution2
dist2 = pdist (np.vstack ([x, y]), 'cosine')

print ('x', x)
print ('y', y)
print ('dist1', dist1)
print ('dist2', dist2)  

参考文献：

http://blog.csdn.net/mr_evanchen/article/details/77511312

https://www.cnblogs.com/denny402/p/7027954.html

http://blog.csdn.net/Kevin_cc98/article/details/73742037