poj Map Labeler 【2-sat + 二分】【最后一道2-sat 1A好开心】

Map Labeler

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1812		Accepted: 597

Description

Map generation is a difficult task in cartography. A vital part of such task is automatic labeling of the cities in a map; where for each city there is text label to be attached to its location, so that no two labels overlap. In this problem, we are concerned with a simple case of automatic map labeling. 

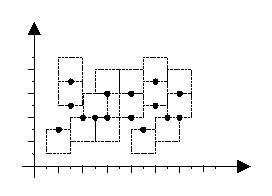
Assume that each city is a point on the plane, and its label is a text bounded in a square with edges parallel to x and y axis. The label of each city should be located such that the city point appears exactly in the middle of the top or bottom edges of the label. In a good labeling, the square labels are all of the same size, and no two labels overlap, although they may share one edge. Figure 1 depicts an example of a good labeling (the texts of the labels are not shown.) 

Given the coordinates of all city points on the map as integer values, you are to find the maximum label size (an integer value) such that a good labeling exists for the map. 

Input

The first line contains a single integer t (1 <= t <= 10), the number of test cases. Each test case starts with a line containing an integer m (3 ≤ m ≤ 100), the number of cities followed by m lines of data each containing a pair of integers; the first integer (X) is the x and the second one (Y) is the y coordinates of one city on the map (-10000 ≤X, Y≤ 10000). Note that no two cities have the same (x, y) coordinates.

Output

The output will be one line per each test case containing the maximum possible label size (an integer value) for a good labeling.

Sample Input

1
6
1 1
2 3
3 2
4 4
10 4
2 5

Sample Output

2

最后一道2-sat了，没想到1A了，真的好开心。题解上点颜色。。。

题意：给你N个城市的坐标，现在你需要为这N个城市贴标签，所有城市的标签是一个正方形且边长相等。

要求1：城市要么在正方形顶边的中间，要么在底边的中间；

要求2：任意两个城市的标签不能重叠（边可以重叠）。

在满足要求的前提下，让你求出正方形的最大边长。

算法实现：二分 + tarjan求SCC判断可行性。

首先我们要知道怎么去判断两个边长相等正方形是否重叠，当然有很多方法，这里我就提一下我的方法：

对于正方形A 它的中心坐标为Xa,Ya

对于正方形B 它的中心坐标为Xb,Yb.

它们的边长都为size

则 两个正方形重叠的充要条件-> |Xa - Xb| < size && |Ya - Yb| < size。这个思路是我灵光一闪想到的。。。

建图思路：感觉比较繁琐，用了容器vector

对于城市i和j，根据它们在顶边中间和底边中间的互相匹配可以得到4中建图方案。

提醒：这里我用i表示i城市坐标在顶边中间，i + N表示坐标在底边中间。

注意：我们在由城市坐标推中心坐标时，边长可能为奇数，因此要size / 2.0。详看代码

一：i，j在顶边中间 不能兼得 

1，G[i].push_back(j + N);//i在顶边中间 j在底边中间 
2，G[j].push_back(i + N);//j在顶边中间 i在底边中间 

二：i，j在底边中间  不能兼得

1，G[i + N].push_back(j);//i在底边中间 j在顶边中间
2，G[j + N].push_back(i);//j在底边中间 j在顶边中间

三：i在顶边中间 j在底边中间  不能兼得

1，G[i].push_back(j);//i在顶边中间 j在顶边中间
2，G[j + N].push_back(i + N);//j在底边中间 i在底边中间

四：i在底边中间 j在顶边中间  不能兼得

1，G[i + N].push_back(j + N);//i在底边中间 j在底边中间
2，G[j].push_back(i);//j在顶边中间 i在顶边中间

AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define MAXN 200+10
#define MAXM 100000
#define INF 1000000
#define DD double
using namespace std;
vector G[MAXN];
int low[MAXN], dfn[MAXN];
int dfs_clock;
int sccno[MAXN], scc_cnt;
stack S;
bool Instack[MAXN];
DD x[MAXN], y[MAXN];//N个城市的坐标 
int N;//N个城市 
void input()
{
	for(int i = 0; i < N; i++)
	scanf("%lf%lf", &x[i], &y[i]);
}
void init()
{
	for(int i = 0; i < 2*N; i++) G[i].clear();
}
bool judge(DD x1, DD y1, DD x2, DD y2, int size)//两个方形重叠 只要它们中心的水平距离和竖直距离都小于边长 
{
	return fabs(x1 - x2) < size && fabs(y1 - y2) < size;
}
void getMap(int size)//根据当前边长 建图 
{
	for(int i = 0; i < N; i++)
	{
		for(int j = 0; j < i; j++)
		{
			//i，j在顶边中间 不能兼得
			if(judge(x[i], y[i] - size / 2.0, x[j], y[j] - size / 2.0, size))
			{
				G[i].push_back(j + N);//i在顶边中间 j在底边中间 
				G[j].push_back(i + N);//j在顶边中间 i在底边中间 
			}
			//i，j在底边中间  不能兼得
			if(judge(x[i], y[i] + size / 2.0, x[j], y[j] + size / 2.0, size))
			{
				G[i + N].push_back(j);//i在底边中间 j在顶边中间
				G[j + N].push_back(i);//j在底边中间 j在顶边中间
			} 
			//i在顶边中间 j在底边中间  不能兼得
			if(judge(x[i], y[i] - size / 2.0, x[j], y[j] + size / 2.0, size))
			{
				G[i].push_back(j);//i在顶边中间 j在顶边中间
				G[j + N].push_back(i + N);//j在底边中间 i在底边中间
			} 
			//i在底边中间 j在顶边中间  不能兼得
			if(judge(x[i], y[i] + size / 2.0, x[j], y[j] - size / 2.0, size))
			{
				G[i + N].push_back(j + N);//i在底边中间 j在底边中间
				G[j].push_back(i);//j在顶边中间 i在顶边中间
			} 
		}
	} 
}
void tarjan(int u, int fa)
{
	int v;
	low[u] = dfn[u] = ++dfs_clock;
	S.push(u);
	Instack[u] = true;
	for(int i = 0; i < G[u].size(); i++)
	{
		v = G[u][i];
		if(!dfn[v])
		{
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
		}
		else if(Instack[v])
		low[u] = min(low[u], dfn[v]);
	}
	if(low[u] == dfn[u])
	{
		scc_cnt++;
		for(;;)
		{
			v = S.top(); S.pop();
			sccno[v] = scc_cnt;
			Instack[v] = false;
			if(v == u) break;
		}
	}
}
void find_cut(int l, int r)
{
	memset(low, 0, sizeof(low));
	memset(dfn, 0, sizeof(dfn));
	memset(sccno, 0, sizeof(sccno));
	memset(Instack, false, sizeof(Instack));
	dfs_clock = scc_cnt = 0;
	for(int i = l; i <= r; i++)
	if(!dfn[i]) tarjan(i, -1);
}
bool two_sat()
{
	for(int i = 0; i < N; i++)
	{
		if(sccno[i] == sccno[i + N])
		return false;
	}
	return true;
}
void solve()//二分查找 
{
	int left, right, mid, ans;
	left = 0, right = 1000000;
	while(right >= left)
	{
		mid = (left + right) / 2;
		init();
		getMap(mid);
		find_cut(0, 2*N-1);
		if(two_sat())
		{
			ans = mid;
			left = mid + 1;
		}
		else
		right = mid - 1;
	}
	printf("%d\n", ans);
}
int main()
{
	int t;
	scanf("%d", &t);
	while(t--)
	{
		scanf("%d", &N);
		input();
		solve();
	}
	return 0;
}