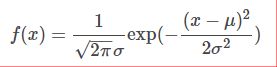通信原理第三章-随机过程
第三章随机过程
基础知识打底:
什么是随机过程:就是所有样本函数的集合 随机过程在任意时刻的值是一个随机的变量,随机过程可以看成是在时间进程中处于不同时刻的随机变量的集合。
随机过程的分布函数:
你不是一个随机变量吗?那你肯定有概率函数,我们取ξ(t)表示一个随机过程,他的分布函数记为F(x1,t1),求导得到概率密度函数。
随机过程的数字特征:
均值方差相关函数自相关函数都回去复习概率论。
-------------------------------------------------------------------------------------------------------------------------------
平稳随机过程:
是什么?一个随机过程的统计特性和时间起点无关,即时间评议不影响其任何统计特性,则称该随机过程是在严格意义下的平稳随机过程,简称严平稳随机过程。
广义平稳需满足两个条件:1均值和时间无关,为常数 2 自相关函数与时间间隔t2-t1有关。
严平稳随机过程一定是广义平稳的,反之不一定成立。
各态历经性
具有各态历经性的过程,其数字特征完全由随机过程中的任意时间的时间平均值来代替。
自相关函数
ξ(t)为平稳随机过程的话,他的自相关函数为 R(τ)=E[ξ(t)ξ(t+τ)]
频谱特性-功率谱密度:随机过程的频谱特性可以用他的功率谱密度表示。
随机过程的任一样本为一个确定的功率型信号,按照对功率信号的功率谱密度定义为: P=lim|X(f)|^2/T. 我们知道非周期的功率信号的自相关系数和他的功率谱密度是一对傅里叶变换,对于平稳随机过程同样成立,即:平稳过程的功率谱密度与其自相关系数也是一对傅里叶变换。
维纳辛钦定理:
对于功率谱密度进行积分能得到平稳过程的平均功率
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
高斯随机过程
正态随机过程,在实际中是主要的噪声-热噪声。随机过程服从正态分布。
一维概率密度函数:
这里有几个函数要特别注意:
正态分布函数:
还有表示高斯曲线尾部下的面积的函数Q、误差函数、互补误差函数:
---------------------------------------------------------------------------------------------------------------------
3.4 平稳随机过程通过线性系统
什么是通过过程:信号通过系统传输的过程。
我们想知道信号输入进去的时候是一个平稳随机过程,经过系统之后的输出信号是否还是一个平稳过程?
我们知道线性时不变系统的输出信号可以由单位冲激响应或者频率响应和输入信号的卷积得到。对应到傅里叶变换就是乘积。
那么利用该关系,假设输入过程是平稳的,均值为a,自相关函数为R,功率谱密度为P, 计算输出过程的
1 均值为a*H(0) H(0)为线性系统在f=0处的频率响应。即直流增益。
2. 自相关系数仅仅是时间间隔的函数,所以是平稳过程。
3.功率谱密度=输入功率谱密度*系统频率响应模值的平方。
4. 概率分布 高斯型分布
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.5 窄带随机过程
窄带随机过程的函数可以写成一个余弦函数和一个正弦函数的差,即同相分量-正交分量。
一个窄带随机变量的均值为0,方差为σ^2,那么他的两个分量的均值和方差与原随机变量相同。除此之外,他的包络的一维分布是瑞利分布,相位的一维分布是均匀分布,而且两者相互独立。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.6 正弦波加窄带高斯噪声
就是一个窄带高斯信号和正弦波加起来。包络的概率密度函数是广义瑞利函数,又称为莱斯函数
高斯白噪声和带限白噪声
什么是白噪声:如果噪声的功率谱密度在所有频率上均为一个常数,则改噪声为白噪声。
如果白噪声取值的概率服从高斯分布,则为高斯白噪声。
低通白噪声:白噪声通过理想矩形的低通滤波器或理想低通信道,则输出的噪声称为低通白噪声。
带通白噪声:
如果白噪声通过理想矩形的带通滤波器或理想带通信道,则其输出的噪声称为带通白噪声。
带通滤波器的B远小于fc,因此也称为窄带滤波器,相应的带通白噪声称为窄带高斯白噪声。
---------------------------------------------------------------------------------------------------------------------------------------------
一个过程是严平稳的,则他必是广义平稳的,反之不一定成立。
时间的时间平均等于对应的统计平稳,则该过程是各态历经性的。
一个过程是各态历经性的,则它也是平稳的,反之不一定成立。
3.7 高斯白噪声和带限白噪声
实际信道或滤波器的带宽存在一定限制,白噪声通过后,其结果是带限噪声,若其谱密度在通带范围内仍具有白色特性, 则称其为带限白噪声,又可分为低通白噪声和带通白噪声。
瑞利分布、莱斯分布、正态分布是通信中常见的三种分布:正弦载波信号加窄带高斯噪声的包络一般为莱斯分布。当信号幅度大的时候,趋近于正态分布,幅度小的时候,近似瑞利分布。