sklearn学习笔记：线性回归预测

1. 获取数据。sklearn中自带一些常用的数据集，点击打开链接，例如用于回归分析的波士顿房价数据集（Boston）、用于分类的鸢尾花数据集（iris）等。现选用Boston数据集，可以先调用shape()等对数据集的基本情况进行查看：

from sklearn import datasets
loaded_data = datasets.load_boston()
data_X = loaded_data.data
data_y = loaded_data.target
print(shape(data_X))
print(shape(data_y))
print(data_X[:2, :])
print(data_y[:2])

输出结果：

(506, 13)
(506,)
[[  6.32000000e-03   1.80000000e+01   2.31000000e+00   0.00000000e+00
    5.38000000e-01   6.57500000e+00   6.52000000e+01   4.09000000e+00
    1.00000000e+00   2.96000000e+02   1.53000000e+01   3.96900000e+02
    4.98000000e+00]
 [  2.73100000e-02   0.00000000e+00   7.07000000e+00   0.00000000e+00
    4.69000000e-01   6.42100000e+00   7.89000000e+01   4.96710000e+00
    2.00000000e+00   2.42000000e+02   1.78000000e+01   3.96900000e+02
    9.14000000e+00]]
[ 24.   21.6]

说明该数据集包括506个样本，每个样本有13个特征值，标签值为房价，同时输出了前两个样本的具体情况。

2.划分训练集和测试集。我们将20%的样本划分为测试集，80%为训练集，即test_size=0.2，同样我们也可以调用shape()来查看划分结果：

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.2)
print(shape(X_train))
print(shape(X_test))

输出结果：

(404, 13)
(102, 13)

3.运行线性模型。我们选用sklearn中基于最小二乘的线性回归模型，并用训练集进行拟合，得到拟合直线y=wTx+b中的权重参数w和b：

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
print (model.coef_)
print (model.intercept_)

输出结果：

[ -1.04864717e-01   3.97233700e-02   1.98757774e-02   2.30896040e+00
  -1.76253192e+01   3.74803039e+00   1.28555952e-04  -1.56689014e+00
   2.97635772e-01  -1.18908274e-02  -9.15199442e-01   1.04446613e-02
  -5.55228840e-01]
36.3527413723

4.模型测试。利用测试集得到对应的结果，并利用均方根误差（MSE）对测试结果进行评价：

y_pred = model.predict(X_test)
from sklearn import metrics
print "MSE:", metrics.mean_squared_error(y_test, y_pred)

输出结果：

MSE: 19.1283413297

5.交叉验证。我们使用10折交叉验证，即cv=10，并求出交叉验证得到的MSE值

from sklearn.model_selection import cross_val_predict
predicted = cross_val_predict(model, data_X, data_y, cv=10)
print  "MSE:", metrics.mean_squared_error(data_y, predicted)

输出结果：

MSE: 34.5970425577

6.画图。将实际房价数据与预测数据作出对比，接近中间绿色直线的数据表示预测准确：

import matplotlib.pyplot as plt
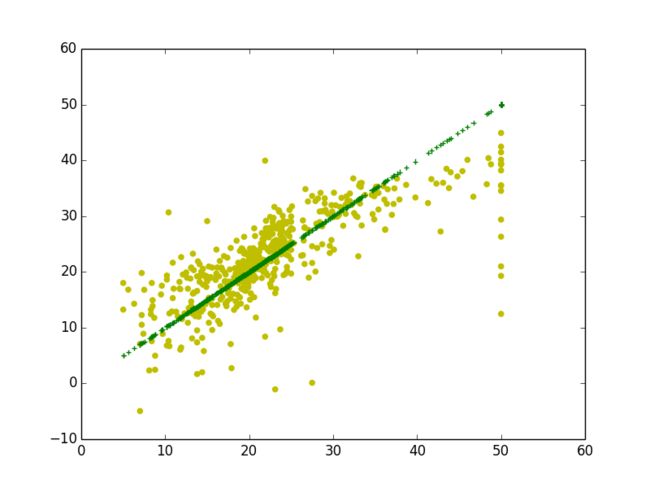
plt.scatter(data_y, predicted, color='y', marker='o')
plt.scatter(data_y, data_y,color='g', marker='+')
plt.show()

输出图像：

7.完整代码为：

from sklearn import datasets
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_predict
from numpy import shape

loaded_data = datasets.load_boston()
data_X = loaded_data.data
data_y = loaded_data.target
# print(shape(data_X))
# print(shape(data_y))
# print(data_X[:2, :])
# print(data_y[:2])

X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, test_size=0.2)
# print(shape(X_train))
# print shape(X_test)

model = LinearRegression()
model.fit(X_train, y_train)
# print (model.coef_)
# print (model.intercept_)

y_pred = model.predict(X_test)
from sklearn import metrics
print "MSE:", metrics.mean_squared_error(y_test, y_pred)

predicted = cross_val_predict(model, data_X, data_y, cv=10)
print  "MSE:", metrics.mean_squared_error(data_y, predicted)

plt.scatter(data_y, predicted, color='y', marker='o')
plt.scatter(data_y, data_y,color='g', marker='+')
plt.show()