hdu 2865 Birthday Toy （置换+DP+矩阵乘法）

Birthday Toy

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 747    Accepted Submission(s): 388

Problem Description

AekdyCoin loves toys. It is AekdyCoin’s Birthday today and he gets a special “Toy”.
The “Toy” is in bulk and AekdyCoin has to make one by him. Let’s assume that the “Toy” has N small white beads and one Big bead .If someone want to make a “Toy”, he (or she) must always puts the Big bead in center, and then connect the other N small beads around it by using N sticks with equal length, and then the N small beads must be connected by N sticks with equal length, and it could be seen as a regular polygon. Figure 1 shows a “Toy” with 8 small white beads and one big white bead.

Now AekdyCoin has C kinds of available color, say blue, green, yellow, pink …etc. He wants to color these beads, but he thinks that must be too boring and stupid. So he colors these beads with one role: any adjacent beads couldn’t have same color. Figure 2 shows a legal situation, and Figure 3 shows an illegal situation.


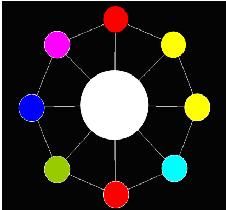
It seems that the “Toy” becomes more interesting for AekdyCoin right now; however, he wants to color the big bead in center. Of course, he should follow the role above.

Now AekdyCoin begins to play with the “Toy”, he always colors the big beads and then the other small beads. He should color under the rule above. After several minutes, AekdyCoin finally makes a perfect “Toy”. Figure 4 shows a situation that is under the color rule.

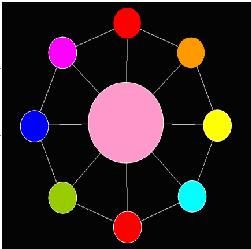
AekdyCoin now want to know the different method to color the “Toy” whit at most K color. (“Toy” contains N small beads and one big bead.)
But, no, the problem is not so easy .The repetitions that are produced by rotation around the center of the circular necklace are all neglected. Figure 5 shows 8 “Toy”, they are regard as one method.


Now AekdyCoin will give you N and K, he wants you to help him calculate the number of different methods, because the number of method is so huge, so AekdyCoin just want you to tell him the remainder when divided by M.
In this problem, M = 1,000,000,007.

 

Input

The input consists of several test cases.(at least 1000)
Every case has only two integers indicating N, K
(3<=N<=10^9, 4<=K<=10^9)

 

Output

For each case, you should output a single line indicates the remainder of number of different methods after divided by M.

 

Sample Input

3 4 3 5 3 17 162 78923

 

Sample Output

8 40 19040 19469065

 

Source

2009 Multi-University Training Contest 7 - Host by FZU

 

Recommend

gaojie   |   We have carefully selected several similar problems for you:   2870  2863  2864  2866  2867 

 

Statistic |  Submit |  Discuss | Note

题目大意：给出上述图形外围的小球的个数，用k种颜色给小球即中间的大球染色，要求有边相连得不能染相同的颜色。求本质不同的染色方案（旋转后相同算是本质相同。）

题解：置换+DP+矩阵乘法

置换f下保持不变的着色方案个数C(f)=k^m(f) m(f)为循环的个数。在置换下保持不变，说明轮换中的点都染了相同的颜色。

之前提到过如果是一个n元环，旋转i，那么循环的个数为gcd(n,i),循环的长度为n/gcd(n,i)

那么我们先假设可以求出f[i]表示i个轮换的染色方案数。

那么答案就是∑(i=1..n)f[gcd(n,i)]。

上面的式子枚举的时间复杂度很高，所以我们考虑不枚举i，枚举循环的长度L.

枚举了L，在计算有多少个i是0<=i<=n并且使L=n/gcd(n,i),即gcd(n,i)=n/L

不妨设a=n/L=gcd(n,i),i=a*t则当且仅当gcd(L,t)=1时，gcd(a*L,a*t)=gcd(n,i)=a

因为0<=i<=n,所以0<=t<=(n/a=L),所以满足条件的t的个数就是phi(L)欧拉函数。

那么∑(i=1..n)f[gcd(n,i)]=∑(L|n)f[n/L]*phi(L)。可以在O(sqrt(n))的时间求解

那么现在的问题就是如何快速的求f。

虽然是i个轮换，其实我们完全可以看成是i个球连成了一个环。相邻的两个颜色不能相同。加入一个轮换相当于在n,1之间插入一个球，那么不能与1,n的颜色相同所以有(k-2)种选择。因为加入一个球的缘故使n与1从原先的不能染相同的颜色变成了可以染相同的颜色，那么我们默认n,1的颜色相同就有(k-1)种旋转。

f[1]=0 f[2]=k*(k-1) f[i]=f[i-1]*(k-2)+f[i-2]*(k-1) 这个式子的话可以用矩阵乘法优化。具体的矩阵可以看程序。

#include
#include
#include
#include
#include
#define N 10000003
#define p 1000000007
#define LL long long 
using namespace std;
int pd[N],prime[N],phi[N],f[3],n; LL k;
struct data{
	LL a[3][3];
}ch,e,b;
void init(int n)
{
	phi[1]=1;
	for (int i=2;i<=n;i++) {
		if (!pd[i]) {
			prime[++prime[0]]=i;
			phi[i]=i-1;
		}
		for (int j=1;j<=prime[0];j++) {
			if(prime[j]*i>n) break;
			pd[i*prime[j]]=1;
			if (i%prime[j]==0) {
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
			else phi[i*prime[j]]=phi[i]*(prime[j]-1);
		}
	}
}
LL getphi(int x)
{
	if (x<=1000000) return (LL)phi[x];
	int ans=x;
	for (int i=1;prime[i]*prime[i]<=x;i++)
	 if (x%prime[i]==0) {
	 	ans=ans/prime[i]*(prime[i]-1);
	 	while (x%prime[i]==0) x/=prime[i];
	 }
	if(x>1) ans=ans/x*(x-1);
	return (LL)ans%p;
}
void clear(data &a)
{
	for (int i=1;i<=2;i++) 
	 for (int j=1;j<=2;j++) a.a[i][j]=e.a[i][j];
}
data mul(data a,data b)
{
	data c;
	for (int i=1;i<=2;i++)
	 for (int j=1;j<=2;j++) {
	 	c.a[i][j]=0;
	 	for (int k=1;k<=2;k++) c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p;
	 }
	return c;
}
data quickpow(data num,int x)
{
	data ans; clear(ans);
	data base; base=num;
	while (x) {
		if (x&1) ans=mul(ans,base);
		x>>=1;
		base=mul(base,base);
    }
 	return ans;
}
LL calc(int i)
{
	if (i<=2) return f[i];
	data t=quickpow(ch,i-2);
	t=mul(b,t);
	return t.a[1][2];
}
LL quickpow(LL num,int x)
{
	LL ans=1; LL base=num%p;
	while (x) {
		if (x&1) ans=ans*base%p;
		x>>=1;
		base=base*base%p;
	}
	return ans;
}
int main()
{
	freopen("a.in","r",stdin);
	init(1000000);
	ch.a[1][1]=0; ch.a[1][2]=1; ch.a[2][1]=1; ch.a[2][2]=1;
	for (int i=1;i<=2;i++) e.a[i][i]=1;
	while (scanf("%d%I64d",&n,&k)!=EOF) {
		k--; f[1]=0; f[2]=k*(k-1)%p;
		b.a[1][1]=f[1]; b.a[1][2]=f[2];
		b.a[2][1]=0; b.a[2][2]=0;
		ch.a[1][1]=0; ch.a[2][1]=1; ch.a[1][2]=k-1; ch.a[2][2]=k-2; 
		LL ans=0; 
		for (int i=1;i*i<=n;i++) 
		 if (n%i==0){
			LL t=calc(n/i); 
			ans+=(LL)t*getphi(i); ans%=p;
			if (i*i!=n) {
				LL t=calc(i);
				ans+=(LL)t*getphi(n/i);
			}
			ans%=p;
		}
		ans=ans*(k+1)%p*quickpow(n,p-2)%p;
		printf("%I64d\n",ans);
	}
}