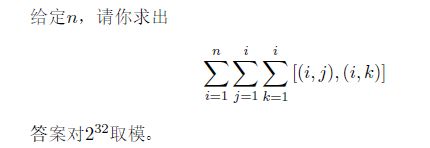【NOI2017模拟3.19】Sum
Description:
n < = 1 e 10 n<=1e10 n<=1e10
题解：
设 f [ i ] = ∑ j = 1 i ∑ k = 1 i [ ( i , j ) , ( i , k ) ] f[i]=\sum_{j=1}^i\sum_{k=1}^i[(i,j),(i,k)] f[i]=∑j=1i∑k=1i[(i,j),(i,k)]
不难（才怪）想到 f [ i ] f[i] f[i]是一个积性函数。
如何快速感性证明：
我们知道 g c d 、 l c m gcd、lcm gcd、lcm都是和每个质因子的指数有关，每一个质因子互不影响，对于这个题显然就是直接乘起来。
然后就是考虑 p k p^k pk怎么做，即枚举 l c m lcm lcm的大小，然后随便写写。
f ( p k ) f(p^k) f(pk)
= ( ∑ i = 0 k − 1 p i ∗ ( p k − p k − i − 1 ) 2 ∗ ( p k − p k − i ) 2 ) + p k ∗ ( 2 ∗ p k − 1 ) =(\sum_{i=0}^{k-1}p^i*(p^k-p^{k-i-1})^2*(p^k-p^{k-i})^2)+p^k*(2*p^k-1) =(∑i=0k−1pi∗(pk−pk−i−1)2∗(pk−pk−i)2)+pk∗(2∗pk−1)
= ( 2 ∗ k + 1 ) ∗ ( p 2 k − p 2 k − 1 ) + p k − 1 =(2*k+1)*(p^{2k}-p^{2k-1})+p^{k-1} =(2∗k+1)∗(p2k−p2k−1)+pk−1
有了这个套个min_25就好了。
Code：
#include