c /c++ 树状数组 入门

  树状数组是十分的优雅的结构，用于解决区间求和，单点修改，树状数组和线段树很相似 ，线段树的使用范围更广，树状数组虽然可用的范围比线段树小但是它的效率比线段树高 

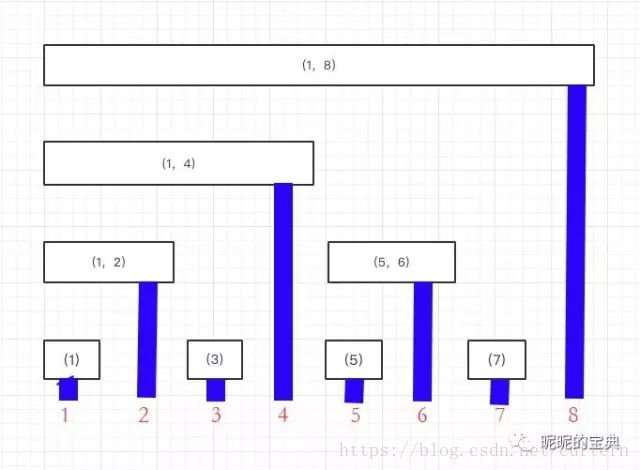
 下面就是树状数组的基本图形，首先要说明的是树状数组是个一维的数组 ，树状数组的下标是从1开始的 而不是从0开始的，我们只是利用了它的下表值的特点，来进行区间的求和，单点修改。 

  1 红色标注的是现在 树状数组的下标

  2   每个红色标注的上方的方格内代表着树状数组能表示原来的数组（ 就是要求和，修改单点的数组 ）

比如 红色下标 2 上方的 （1，2） 表示了他代表的是原来数组从 a[1] 一直到a[2]的和 （假设原来的数组为 a[8])

再比如 红色下标3 上方的 （3） ， 就表示他代表的是原来数组 a[3]  （只有一个就不用再说求和了。。。）

看下面这个表格  ，要注意的是 树状数组巧妙地利用了 二进制数的特点 。

  这个图和上边的 图是相互对应的 ，观察到一下的特点

    1 . 节点下表和第四列的 最后一个元素是一样的 （就是树状数组的一个节点 所表示的范围的最后一个元素）。

    2. 节点对应的元素个数是 节点下标的二进制中从右到左的0的个数 的二次方，也就是从右到左有k个0，那么能表示的

个数就是2^k , 比如1的二进制 k =0,所以它能表示的个数是2^0 (就是1个).  再比如6的二进制 0110 , k  = 1所以它能表示的个数就是 2个。

   3 . 每个节点所能表示的原来数组（ 就是要求和，修改单点的数组 ）的下标都是连续的。

 

 一 . 在了解树状数组的这些特性之后我们来看一下 树状数组很重要的 lowbit（) 这个函数

 int lowbit(int x){

    return x&(-x);  

}

下面这个证明说的很详细

首先明白一个概念，计算机中-i=（i的取反+1），也就是i的补码 
而lowbit，就是求（树状数组中）一个数二进制的1的最低位，例如01100110，lowbit=00000010；再例如01100000，lowbit=00100000。 
所以若一个数（先考虑四位）的二进制为abcd，那么其取反为(1-a)(1-b)(1-c)(1-d)，那么其补码为(1-a)(1-b)(1-c)(2-d)。 
如果d为1，什么事都没有-_-|||但我们知道如果d为0，天理不容2Σ( ° △ °|||)︴ 
于是就要进位。如果c也为0，那么1-b又要加1，然后又有可能是1-a……直到碰见一个为补码为0的bit，我们假设这个bit的位置为x 
这个时候可以发现：是不是x之前的bit的补码都与其自身不同？，x之后的补码与其自身一样都是0？ 
例如01101000，反码为10010111，补码为10011000，可以看到在原来数正数第五位前，补码的进位因第五位使其不会受到影响，于是0&1=0,； 
但在这个原来数“1”后，所有零的补码都会因加1而进位，导致在这个“1”后所有数都变成0，再加上0&0=0，所以他们运算结果也都是零； 
只有在这个数处，0+1=1，连锁反应停止，所以这个数就被确定啦O(∩_∩)O 

所以and以后只有x这个bit是一……

 

二 .  知道了lowbit  .  在看 树状数组的就和的函数 getsum  ，树状数组为A[8], 要注意的是树状数组的大小和原来数组的大小是一样的。 原型如下：

int getsum(int x){
   int s = 0;

    while(x > 0){

             s+=A[x];

            x-=lowbit(x);  }

    return s; }

可能有人不太明白getsum 为什么 只求每次下标为 x 减去lowbit(x) 的和，可以看一下上面的图

比如要求原来数组的前6项和，也就是 getsum（6）；6 的二进制是 0110 吧  ,带入getsum中

在第一次进入到while循环的时候 s = s+ A[6], 可以看上面的图 A[6] = a[5]+a[6]; 也就是s 现在等于a[5] + a[6]了 ，然后

x = x-lowbit(x), 希望大家了解了lowbit（x）的作用， lowbit（6） = 0010 ， 原来的 6是0110， 这样 6 - lowbit（6） = 010 0 ，也就是x = 0100 = 4； 

然后x > 0  , 第二次进入while ， 这时候 s = s + A[4] ,看上图的 A[4] = a[1] + a[2] + a[3] + a[4], 这样s = a[1] + a[2] + a[3] + a[4] + a[5] + a[6]  ， 然后 x = x - lowbit(x),    lowbit(4) = 0100 , 4 = 0100,   4 - lowbit(4) = 0;   所以x = 0 然后 就不再进入while ， 也求出了 getsum（6）， 这就是getsum（）的原理。 

 

三.  然后就是另外一个 函数 update()    ，原型如下 

void update(int x,int num){

      while(x <= n){

            A[x] +=num;

            x +=lowbit(x);

 }

这个函数的作用就是当修改了 原来一个数组的一个值的时候，通过这个函数来维护树状数组的值，树状数组的时间复杂度是 O（log n) , 因为树状数组是围绕这二进制进行修改的 n的二进制最多是 log n 个 所以复杂度为log n ，

update()的原理和 getsum（）是一样的 ，当你修改了 原来数组的a[3]吧 你就要修改 所有包括a[3]的树状数组，而寻找包含a[3]的树状数组就是通过 x += lowbit(x) , 同样观察上边的图就可以看出来，

 

敌兵布阵

http://acm.hdu.edu.cn/showproblem.php?pid=1166

#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 50010;
int A[maxn];
int n;
int T;
int ot[maxn];
int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int num)
{
    while(x <= n)
    {
    A[x]+=num;
    x+=lowbit(x);
    }
}
int getsum(int x)
{
    int sum = 0;
    while(x > 0)
    {
        sum+=A[x];
        x-=lowbit(x);
    }
    return sum;
}
int main()
{
    cin>>T;
    for(int cur = 1; cur <= T;cur++)
    {
        cin>>n;
        memset(A,0,sizeof A);
        for(int i = 1; i <=n ;i++)
        {
            int a;
            cin>>a;
            update(i,a);
        }
        char ch[10];
        int i,j;
        getchar();
        scanf("%s",ch);
        int ans = 0;
        while(strcmp(ch,"End"))
        {
            cin>>i>>j;
            if(ch[0] == 'A')
                update(i,j);
            else if(ch[0] == 'S')
                update(i,-j);
            else
                ot[ans++] = getsum(j) - getsum(i - 1);
            getchar();
            scanf("%s",ch);
        }
        cout<<"Case "<