雅礼集训2017Day5 远行
Description
Miranda 生活的城市有 N个小镇,一开始小镇间没有任何道路连接。随着经济发现,小镇之间陆续建起了一些双向的道路但是由于经济不太发达,在建设过程中,会保证对于任意两个小镇,最多有一条路径能互相到达。有的时候 Miranda 会从某个小镇开始进行徒步旅行,每次出发前,她都想选择一个她能到达的最远的小镇作为终点,并且她在行走过程中是不会走回头路的,为了估算这次旅行的时间,她会需要你告诉她这次旅行的时间会是多少呢?可以假设通过每条道路都需要单位时间,并且 Miranda 不会在小镇停留。
Input
第一行一个整数 type,表示数据类型。
第二行两个整数 N、Q。
接下来 Q 行,每行先读入一个整数 t,若 t=1,则接下来读入两个整数 u、v,表示小镇 u与小镇 v 建立了一条新道路。若 t=2,读入一个整数 u,表示 Miranda 要开始一次从小镇 u出发的旅行。
若 type=1,记 lastAns表示最近一次 Miranda 旅行的时间,那么对于每次操作的 u或 u,v,都要异或上 lastAns。
若 type=0,则不需要对数据进行处理。
Output
对于每次询问,输出 Miranda 能到达的最远的小镇的距离是多少。注意 Miranda 可能只能留在开始的小镇。
Sample Input
0
5 10
1 4 5
2 3
2 5
2 1
1 5 3
1 1 4
2 3
2 5
1 5 2
2 1
Sample Output
0
1
0
3
2
3
Hint
【数据范围及约定】
对于 20%的数据,N≤5000,Q≤10000;
对于 50%的数据,N≤100000,Q≤200000;
对于另外 20%的数据,type=0;
对于 100%的数据,N≤300000,Q≤500000,type∈{0,1},解密后的 u、v满足 1≤u,v≤N,且道路的修建会满足:每一时刻,都不存在 u,v 使得 u,v之间能通过多种方式到达。
LCT维护树的直径。
给个结论(比较显然):
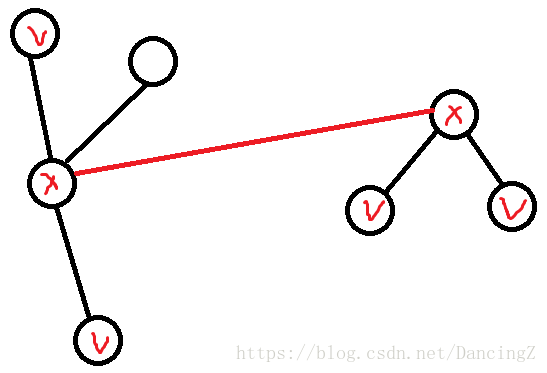
两个树合并在一起,新树直径的两个端点一定在原来两棵树的直径4个端点中。
如上图,打钩的为4个直径端点。对于树中的任意点,两个直径点分别是其向上和向下最大的路径,因此,加入一条边之后原树距离不变,对于打x的点来说,向上和向下的最长距离仅可能在原树4个直径端点变化。将向上和向下的最长距离拼起来就得到直径。
一共讨论6种情况。
#include
using namespace std;
#define Inc(i,L,r) for(register int i=(L);i<=(r);++i)
const int N = 3e5+10;
int n,m,las,type;
int L[N],r[N],fa[N];
inline int findfa(int x){
return x^fa[x]?fa[x]=findfa(fa[x]):x;
}
struct Splay{
int siz[N];
bool rev[N];
int p[N],ch[N][2];
#define Ls(v) ch[v][0]
#define rs(v) ch[v][1]
inline bool is_root(int x){
return (Ls(p[x])^x)&&(rs(p[x])^x);
}
inline void pushdown(int x){
if(rev[x]){
rev[Ls(x)]^=1,rev[rs(x)]^=1;
swap(Ls(x),rs(x));
rev[x]=0;
}
}
inline void maintain(int x){
siz[x]=siz[Ls(x)]+siz[rs(x)]+1;
}
inline void rot(int x){
int f=p[x],gf=p[f],type=rs(f)==x,son=ch[x][!type];
if(!is_root(f))ch[gf][rs(gf)==f]=x;p[x]=gf;
ch[p[son]=f][type]=son,maintain(f);
ch[p[f]=x][!type]=f,maintain(x);
}
int top,stk[N];
inline void splay(int x){
stk[++top]=x;
if(!is_root(x))for(int i=x;!is_root(i);i=p[i])stk[++top]=p[i];
while(top)pushdown(stk[top--]);
while(!is_root(x)){
if(is_root(p[x]))return rot(x),void();
if((rs(p[p[x]])==p[x])==(rs(p[x])==x))rot(p[x]);
rot(x);
}
}
};
struct LCT{
Splay sp;
inline void access(int x){
for(int lastx=0;x;lastx=x,x=sp.p[x])
sp.splay(x),sp.rs(x)=lastx,sp.maintain(x);
}
inline void make_root(int x){
access(x),sp.splay(x),sp.rev[x]^=1;
}
inline void link(int x,int y){
make_root(x),sp.p[x]=y;
}
inline void split(int x,int y){
make_root(x),access(y),sp.splay(y);
}
inline int calc(int x,int y){
return split(x,y),sp.siz[y]-1;
}
}lct;
inline void init(){
scanf("%d%d%d",&type,&n,&m);
Inc(i,1,n)L[i]=r[i]=fa[i]=i;
}
inline void Work(int x,int y){
int sx=findfa(x),sy=findfa(y);
int ndis=-1,tmp,nL,nr;
tmp=lct.calc(L[sx],r[sx]);if(tmp>ndis)ndis=tmp,nL=L[sx],nr=r[sx];//思路清晰。。。
tmp=lct.calc(L[sx],L[sy]);if(tmp>ndis)ndis=tmp,nL=L[sx],nr=L[sy];//注意不要写错L,r
tmp=lct.calc(L[sx],r[sy]);if(tmp>ndis)ndis=tmp,nL=L[sx],nr=r[sy];
tmp=lct.calc(r[sx],L[sy]);if(tmp>ndis)ndis=tmp,nL=r[sx],nr=L[sy];
tmp=lct.calc(r[sx],r[sy]);if(tmp>ndis)ndis=tmp,nL=r[sx],nr=r[sy];
tmp=lct.calc(L[sy],r[sy]);if(tmp>ndis)ndis=tmp,nL=L[sy],nr=r[sy];
fa[sx]=sy;L[sy]=nL,r[sy]=nr;
}
inline void solv(){
while(m--){
int op,x,y;scanf("%d",&op);
switch(op){
case 1:
scanf("%d%d",&x,&y);if(type)x^=las,y^=las;
lct.link(x,y);
Work(x,y);
break;
case 2:
scanf("%d",&x);if(type)x^=las;
int sx=findfa(x);
cout<<(las=max(lct.calc(L[sx],x),lct.calc(x,r[sx])))<<"\n";
break;
}
}
}
int main(){
init();
solv();
return 0;
}