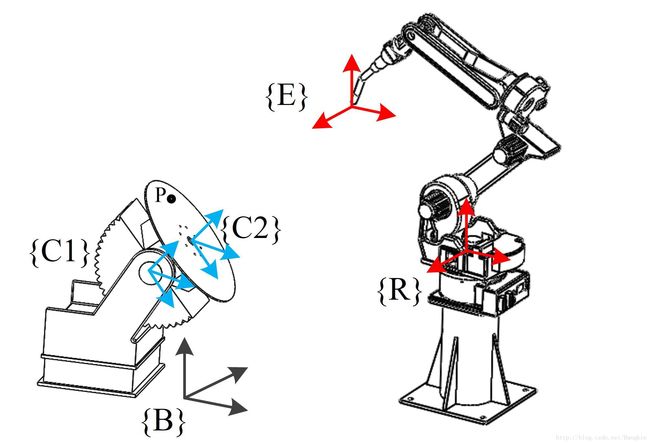
机器人与变位机协调轨迹仿真

复杂空间轨迹的焊接一般需要变位机的参与，加入变位机能够尽量保证焊缝处于船型焊状态，有利于焊缝成型。本文通过机器人与变位机的耦合关系，分析变位机与机器人的协调运动，并对空间相贯线进行仿真。

---

耦合关系

运动链的建立，如图：

---

RTB⋅BTC1⋅C1TC2⋅C2TP⋅Pc=RTE⋅Pr

---

空间相贯线

轴线相交的相贯线方程为：

⎧⎩⎨⎪⎪⎪⎪x=r∗cos(θ)y=r∗sin(θ)z=R2−r2∗sin(θ)2−−−−−−−−−−−−−−√

将其轨迹转化到变位机卡盘坐标系中，本例中默认两轴线相交位置为卡盘坐标系原点。相贯线轨迹相对于卡盘坐标系为定值。

---

坐标系变换-解耦

机器人跟踪时需要得到焊缝点在机器人坐标系下的位置，故需要将上述得到的相贯线轨迹转化到机器人坐标系下：

RTB⋅BTC1⋅C1TC2⋅C2TP⋅Pc=P

其中 RTB 为固定矩阵，通过机器人标定变位机位置得到； BTC1 和 C1TC2 为变位机内部轴变换关系，与各自轴的转角相关； C2TP 为固定矩阵，安装后位置不变，通过机器人焊枪可以测得P点的位置，通过矩阵变换可以得到每个焊缝点相对卡盘的位置。得到相对位置后就能够通过转角的变化获得焊缝点在不同转角情况下在机器人坐标系中的位置。

---

相贯线轨迹仿真实例

• 初始相贯线位置

%相贯线轨迹在卡盘坐标系下位置
X=[];
Y=[];
Z=[];
R=200;r=100;
for i=0:1:180
    x1 = r*cosd(i);
    y1 = r*sind(i);
    z1 = sqrt(R*R-r*r*sind(i)*sind(i));
    X=[X x1];
    Y=[Y y1];
    Z=[Z z1];
end

• 机器人坐标系中位置

%相贯线轨迹在机器人坐标系下位置
X1=[];Y1=[];Z1=[];
for j=1:1:size(X,2)
    P=[X(j) Y(j) Z(j)];         %初始时的位置
    H1=coordinate(b,a1,a2,P);   %使用绝对角度更新移动后的位置
    X1=[X1 H1(1,4)];
    Y1=[Y1 H1(2,4)];
    Z1=[Z1 H1(3,4)];
 end

其中coordinate函数完成的就是坐标系变换的过程，即

RTB⋅BTC1⋅C1TC2⋅C2TP⋅Pc=P

---

• 变位机运动

for i=0:1:61
    a1=0.5*i*pi/180;   %只设定1轴运动
    a2=-0*i*pi/180;

    X2=[];Y2=[];Z2=[];       %每次移动后更新的所有焊缝点位置
    for j=1:1:size(X,2)
        P=[X(j) Y(j) Z(j)];         %初始时的位置(卡盘坐标系）
        H1=coordinate(b,a1,a2,P);   %使用绝对角度更新移动后的位置
        X2=[X2 H1(1,4)];
        Y2=[Y2 H1(2,4)];
        Z2=[Z2 H1(3,4)];
    end
end

---

• 机器人跟踪
  采用船型焊接，那么焊接点处焊缝的切线方向应该保持水平方向，以此作为约束条件，对机器人的运动进行跟踪仿真。
  在上述循环中，加入如下代码：

   dz1 = diff(Z2);             %差分，计算近似切线
   [zm1,m1]=min(abs(dz1(1:1:m+5))); %寻找切线水平的焊缝点在更新轨迹中的位置
   P1=[X2(m1) Y2(m1) Z2(m1)];
   plot3(P1(1),P1(2),P1(3),'-*r','MarkerSize',5);

以上代码将每次变换后的水平位置显示出来，表示机器人在当前位置下跟踪的焊缝点。

---

• 跟踪结果
  
  如图表示的是不同时刻下跟踪情况，初始时刻，最下方的蓝色轨迹表示的是初始相贯线在机器人坐标系中的位置，红色点表示机器人跟踪点。随着变位机运动，机器人运动到最近的切线近似水平的点，绿色箭头表示切线方向，基本保持水平。

---

本文只是对机器人和变位机运动跟踪的初步仿真，并没有考虑到机器人运动的速度。由于最近需要采用视觉传感器协调跟踪焊缝，故先进行了一个简单的仿真实验。机器人与变位机的协调运动在当前主流的机器人系统中都有相应的功能，所以这个部分也不是本人研究的内容，当然我的研究内容也需要在协调运动的基础上进行机器人的纠偏控制，通过这个仿真实验也算对视觉纠偏控制有了一些思路。