ACM算法:线段树
线段树的用途:线段树,顾名思义,就是对线段序列按照树的方式进行操作。这样,线段序列就可以摒弃查询,增加等
操作中的遍历而导致的低效率,从而得到树状结构的log(N)的时间复杂度的优化。
线段树一般用于计算线段序列中,某区间元素数的总和,而且这个线段序列是经常进行改动操作的,这个时候,你就要
不断的对序列中的每个元素进行更新,并不断的遍历。一般的遍历做法明显不能满足我们的需求,这个时候我们就会想
到树。而线段树就是解决这类问题的。当然我们可以对其进行改造,使它能适用于查询等其他操作。
有一种和线段树的用途相似的算法,叫“树状数组”,但是这个比较难理解,我的另一篇博客对其进行了解释。
线段树的思路:如果你熟练二分查找或者了解过,那么理解线段树应该不会有很大的问题,因为线段树所利用的核心思想和
二分搜索差不多,只是我们在其中进行了一些改造和优化。
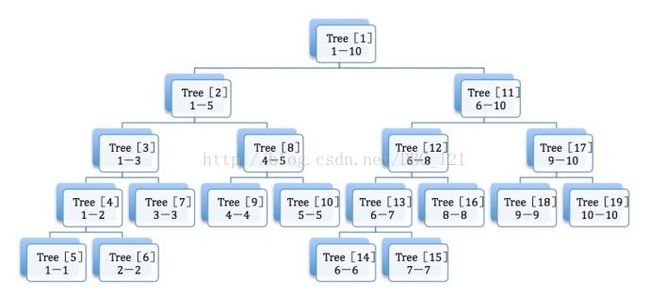
它的思路是利用一个树状结构,将整个线段序列进行二分操作,每个节点保存一个二分区间内元素的总和,进而我们每次修
改某个元素的时候,只要对该节点以及这个节点所在的树状分支上的结点进行就该即可,这样,我们的操作复杂度就降到了
log(N)。
如果没有理解我上面的那段话,我这里从网上捞了一张图,便于理解。
线段树的实现:虽然我们的思想是用树状结构实现的,但我们其实只用一个比原元素数组(source[N])容量
大四倍的数组(tree[4 * N])就行,正所谓逻辑结构和真正的物理结构是不一样的。接着你可能已经意识到了,
逻辑树结构中,每个结点所要保存的内容,分别有value(该区间的元素总和)、left(该区间的左端点下标)、
right(该区间右端点下标)、add(储存每次改变的值)。这就需要一个结构体来实现了。
struct Node {
int left, right; //标记区间的左右端点
int value; //标记这个区间元素的总和
int add; //标记每次操作的那个区间的改变量
}tree[4 * Max];
//tree用于存放线段树,因为是模拟树状结构,所以空间
//最好是元素总和的四倍。
可能value、left、right都好理解,但是为什么要add呢?,原因在于,我们实现线段树的时候一般还会加上一段
优化代码,这段代码是如何优化的,在代码里解释会更加清楚。
const int Max = 100;
struct Node {
int left, right; //标记区间的左右端点
int value; //标记这个区间元素的总和
int add; //标记每次操作的那个区间的改变量
}tree[4 * Max];
//tree用于存放线段树,因为是模拟树状结构,所以空间
//最好是元素总和的四倍。
int source[Max]; //存放初始化的元素的数组
void build(int x, int L, int R)
{
tree[x].left = L;
tree[x].right = R;
if (L == R) {
tree[x].value = source[L];
return;
}
int mid = (L + R) / 2;
build(x * 2, L, mid);
build(x * 2 + 1, mid, R);
tree[x].value = tree[x * 2].value + tree[x * 2 + 1].value;
tree[x].add = 0;
}
void updata(int x, int L, int R, int m)
{
tree[x].value += (R - L + 1) * m;
if (tree[x].left == L && tree[x].right == R) {
tree[x].add += m;
return;
}
if(tree[x].add) {
tree[x * 2].add += tree[x].add;
tree[x * 2].value += (tree[x * 2].right - tree[x * 2].left + 1) * tree[x].add;
tree[x * 2 + 1].add += tree[x].add;
tree[x * 2 + 1].value += (tree[x * 2 + 1].right - tree[x * 2 + 1].left + 1) * tree[x].add;
tree[x].add = 0;
}
int mid = (tree[x].left + tree[x].right) / 2;
if (R <= mid) {
updata(x * 2, L, R, m);
}
else if (L >= mid) {
updata(x * 2 + 1, L, R, m);
}
else {
updata(x * 2, L, mid, m);
updata(x * 2 + 1, mid, R, m);
}
}
int ptr = 0;
void query(int x, int L, int R)
{
if (tree[x].left == L && tree[x].right == R) { //找到目标区间,则立刻返回
ptr += tree[x].value;
return;
}
if (tree[x].add) {
tree[x * 2].add += tree[x].add;
tree[x * 2].value += (tree[x].right - tree[x].left + 1) * tree[x].add;
tree[x * 2 + 1].add += tree[x].add;
tree[x * 2 + 1].value += (tree[x].right - tree[x].left + 1) * tree[x].add;
tree[x].add = 0;
}
int mid = (tree[x].right - tree[x].left + 1) / 2;
if (R <= mid) {
query(x * 2, L, R);
}
else if(L >= mid) {
query(x * 2 + 1, L, R);
}
else {
query(x * 2, L, mid);
query(x * 2 + 1, mid, R);
}
}
/*仔细看updata函数和equry函数,你就会发现会有同样的一段代码,就是上面划红线的代码。
脑补这两个函数你就会发现,初次使用updata函数的时候,也就是add在初次被改变的时候,
这段代码都是会跳过不运行的,而当你以后再次调用函数的时候,add已经被改变的基础之上,
这段代码就会被运行,从而更新该节点所连接的后续结点。为什么这样做?这样使得每次更新
数据时,在该结点及其子树全部更新数据后,再在该结点的增量add上+b,这样在每次查询或
更新到它的子结点时,必然会遍历到该结点,此时查询该结点的add是否为0,如果不为0,则
将add的值向下传递,更新子树结点上的value。
毕竟在需要时才进行更新是一个很好的算法优化
*/总结:线段树还是比较好理解的,对于add的这个优化方法,只要稍加理解就不算什么问题。而线段树的高效摆在那,
是我们需要掌握的一种算法。当然有一种比线段树更加优秀的算法——树状数组,也可以学习学习(请见我另一篇博客)。