每周训练 题解

#A
从题目的第一行中可以很容易看出,这题用的是扩展欧几里得算法$i\ast a+j\ast b=n+1$，因为要保证$i\ast a$,$j\ast b$为正整数，所以i，j必须为正整数。所以这题就求i，j的解为正整数的解的个数。没有看着来说明你对这个算法还不够了解。
求正整数解的个数的时候我是求出i的最小正整数解，再用i求出对应的j，接下来假设我们让i增加（i必然满足情况），那么j必然减小，所以让j除以j的每次的减少量，就可以直接的求出正整数解的个数。注意0不能取。

#include 
#define pi acos(-1)
#define pb push_back
#define LL long long
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define local freopen("in.txt","r",stdin)
#define input_fast std::ios::sync_with_stdio(false);std::cin.tie(0)
using namespace std;
const int mod = 1e9 + 7;
const int INF=0x7FFFFFFF;
inline void read(int& x){
    int flag = 1; char c; while(((c = getchar()) < '0' || c > '9') && c != '-');
    c == '-' ? (flag = -1, x = 0) : (x = c - '0');
    while((c = getchar()) >= '0' && c <= '9') { x = x * 10 + c - '0'; } x *= flag;
}

void exgcd(LL a, LL b, LL &d, LL &x, LL &y){
    if(b == 0){ d = a; x = 1; y = 0; return;}
    exgcd(b, a % b, d, y, x); y -= a / b * x;
}

int main(){
    input_fast;
    //local;

    int t; LL n, a, b, d, x, y; cin >> t; while(t--){
        cin >> n >> a >> b; ++n;
        exgcd(a, b, d, x, y);
        if(n % d){ cout << 0 << endl; continue;}
        x *= n / d; x = (x % (b / d) + b / d) % (b / d);
        if(x == 0) x += b / d;
        y = (n - x * a) / b;
        if(y <= 0) cout << 0 << endl;
        else cout << y / (a / d) + (y % (a / d) ? 1 : 0) << endl;
    }
    return 0;
}

抛开这个题我们发现题目给的集合就是a，b都为1时的正整数解集，当a，b取不同值可能导致解集缩小（成为它的子集，虽然这样说不严谨），想想这个有助于你理解扩展欧几里得求通解的过程。
#B
N(n)就是[Partition](https://en.wikipedia.org/wiki/Partition_(number_theory)
我们从中发现了和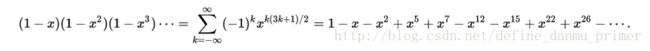再结合题目中给的公式，就可以得出$x^n$的系数序列为1，-1，-1，0，0，1，0，1···，而x的幂的取值为$k(3k+1)/2$,k为0，-1，1，-2，2···，具体工程看代码。

#include 
#define pi acos(-1)
#define pb push_back
#define LL long long
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define local freopen("in.txt","r",stdin)
#define input_fast std::ios::sync_with_stdio(false);std::cin.tie(0)
using namespace std;
const int INF = 0x7FFFFFFF;
const int mod = 1e9 + 7;
inline void read(int& x){
    int flag = 1; char c; while(((c = getchar()) < '0' || c > '9') && c != '-');
    c == '-' ? (flag = -1, x = 0) : (x = c - '0');
    while((c = getchar()) >= '0' && c <= '9') { x = x * 10 + c - '0'; } x *= flag;
}

int a[52000], cnt;
void init(){
    a[cnt++] = 0;
    for(int i = 1; true; ++i){
        a[cnt++] = (-i) * ((-i) * 3 + 1) / 2;
        if(a[cnt - 1] >= mod) break;
        a[cnt++] = i * (i * 3 + 1) / 2;
        if(a[cnt - 1] >= mod) break;
    }
    //cout << cnt << endl; 51641
}

LL power(LL a, int b){
    LL res = 1;
    while(b){
        if(b & 1) res = (res * a) % mod;
        a = a * a % mod; b >>= 1;
    }
    return res;
}

int main(){
    input_fast;

    init();
    int t, base, n, coe, index; LL ans = 0; read(t); read(base);
    for(int i = 1; i <= t; ++i){
        read(n);
        index = lower_bound(a, a + cnt, n) - a;
        if(a[index] == n){ if(index % 4 == 0 || index % 4 ==3) coe = 1; else coe = -1;}
        else coe = 0;
        if(coe == 1) ans = (ans + power(base, t - i)) % mod;
        else if(coe == -1) ans = (ans + 998244352 * power(base, t - i)) % mod;
    }
    cout << ans << endl;
    return 0;
}

#C
题解的证明，我还没有理解，大家先凑合看

#D
这题我挂错了
#E
n堆糖果，每人可以从一堆中取任意多个(大于0)或者把一堆分成三堆，所以

sg（0）=0，
sg（1）=1，
sg（2）=2，
sg（3）=3
。
。
。
sg（7）=8；
sg（8）=7；
sg（9）=9；
。
。
。
sg（8k+1）=8k+1,
sg（8k+2）=8k+2,
.
.
.
sg（8k+7）=8k+8,
sg（8k+8）=8k+7,k>=0;
同样分成两堆的时候是
sg（4k+1）=4k+1,
sg（4k+2）=4k+2,
.
.
.
sg（4k+3）=4k+4,
sg（4k+4）=8k+3,k>=0;