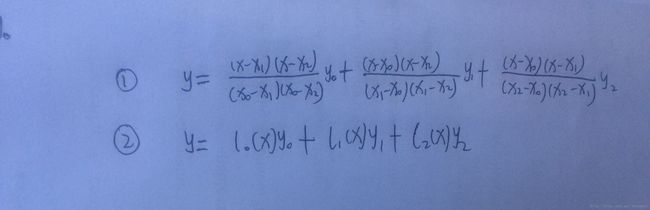拉格朗日插值法 【python】
一、插值
设函数y=f(x)在区间[a,b]上连续,给定n+1个点
a≤x0
已知,f(xk)=yk(k=0,1....n),在函数类P中寻找一个函数Φ(x)。作为f(x)的近似表达式,使满足:
Φ(xk)=f(xk)=yk, k=0,1,2,3,4....n (2)
f(x)为被插值函数,Φ(x)为插值函数,x0,x1....xn为插值节点。(2)为插值节点。
二、拉格朗日插值法
线性插值:拉格朗日插值法中最简单的是线性插值,我们先来了解线性插值函数的构成。在此基础上了解多次插值,
已知两点(x0,y0)和(x1,y1),这里f(x0)=y0,f(x1)=y1,通过这两个点的插值多项式是一条直线,如下:
(x-x1)/(x0-x1)*y0+(x-x0)/(x1-x0)*y1 可以看出当x=x0的时候,函数值y0,当x=x1的时候,函数值为y1.
多项插值
在线性插值中,仅仅用到了两个点,为了提高精度,我们希望用更多的点来提高精度。为此我们用三个点来做插值
已知点(x0,y0),(x1,y1),(x2,y2).如下图所示,式1是两次的拉格朗日插值函数。式2是拉格朗日函数的一般形式。
当x=x0的时候,l0(x)的值为1,l1(x)的值为0,l2(x)的值为0.最后函数值为y0.
拉格朗日插值的函数的形式都是如式二所示。假设有n个点进行拉格朗日插值。则插值函数一共有n项,每一项都是ln(x)*yn (n的取值为1到n),当x=m的时候(m为1到n中的数时),相应的ln(x)为一,其他项为0。函数值为ym.
但是,我们应该如何求解ln(x)呢。以上面的三个点为例,在求l0的时候,分子为x减去除了x0的点的连乘,分母为x0减去除x0点的连乘。其他的项也是这样计算的。
三、拉格朗日插值法的python应用
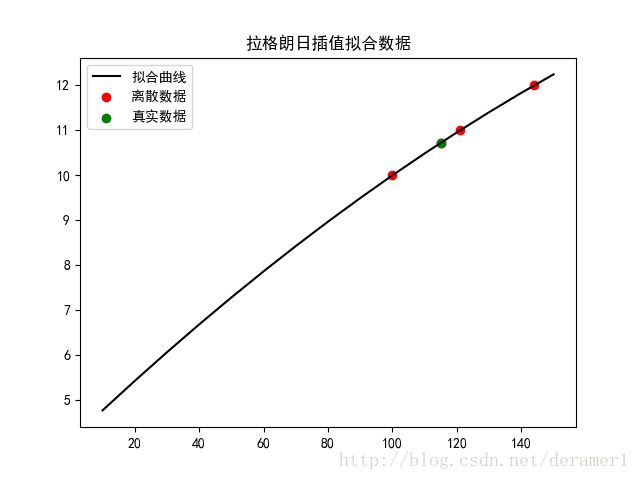
下面的程序是求点(100,10),(121,11),(144,12),可以看出函数为根号x,现在用拉格朗日插值法求三个点的插值函数,并绘制出函数图像,并求将根号115对应的函数值画在同一坐标系中,观察拉格朗日插值法的精确度。
import matplotlib.pyplot as plt
from pylab import mpl
"""
用拉格朗日插值法拟合数据。
"""
"""
功能:计算插值多项式的系数。
参数:data_x为数据的x坐标,data_y为数据的y坐标,size为插值基函数的个数。
返回值:插值函数的系数。
"""
x = [100, 121, 144]
y = [10,11, 12]
def ParametersOfLagrangeInterpolation(data_x,data_y,size):
parameters=[]
#i用来控制参数的个数
i=0;
while i < size:
#j用来控制循环的变量做累乘
j = 0;
temp = 1;
while j < size:
if(i != j):
temp*=data_x[i]-data_x[j]
j+=1;
parameters.append(data_y[i]/temp)
i += 1;
return parameters
"""
功能:计算拉格朗日插值法公式的值。
参数:data_x为原始数据的横坐标,x为要用拉格朗日插值函数计算数据,parameters为拉格朗日插值函数的系数。
返回值:经拉格朗日插值公式计算后的值。
"""
def CalculateTheValueOfLarangeInterpolation(data_x,parameters,x):
returnValue=0
i = 0;
while i < len(parameters):
temp = 1
j = 0;
while j< len(parameters):
if(i!=j):
temp *=x-data_x[j]
j+=1
returnValue += temp * parameters[i]
i += 1
return returnValue
"""
功能:将函数绘制成图像
参数:data_x,data_y为离散的点.new_data_x,new_data_y为由拉格朗日插值函数计算的值。x为函数的预测值。
返回值:空
"""
def Draw(data_x,data_y,new_data_x,new_data_y):
plt.plot(new_data_x, new_data_y, label="拟合曲线", color="black")
plt.scatter(data_x,data_y, label="离散数据",color="red")
plt.scatter(115, 10.723805294764, label="真实数据", color="green")
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("拉格朗日插值拟合数据")
plt.legend(loc="upper left")
plt.show()
"""
由于三个点绘制的拟合曲线效果太差,所以采用这样的方法来进行数据拟合。
1>利用原数据计算出拉格朗日插值多项式的函数,分别在10-150区间内,每10个数取一个点,计算相应的值,绘制函数图像。
2>将源数据以点的形式画在图像上,
3>将115代入拉格朗日函数计算出相应的值,绘制在图像上。点为红色。并将真实的值也绘制在图像上点为绿色。看红色的点和绿色的点是否重合。
4>结果证明红色的点和绿色的点重合,说明拉格朗日函数插值效果较好。
"""
parameters=ParametersOfLagrangeInterpolation(x,y,3)
datax=[10,20,30,40,50,60,70,80,90,100,110,120,130,140,150]
datay=[]
for temp in datax:
datay.append(CalculateTheValueOfLarangeInterpolation(x,parameters,temp))
x.append(115)
y.append(CalculateTheValueOfLarangeInterpolation(x,parameters,115))
Draw(x,y,datax,datay)