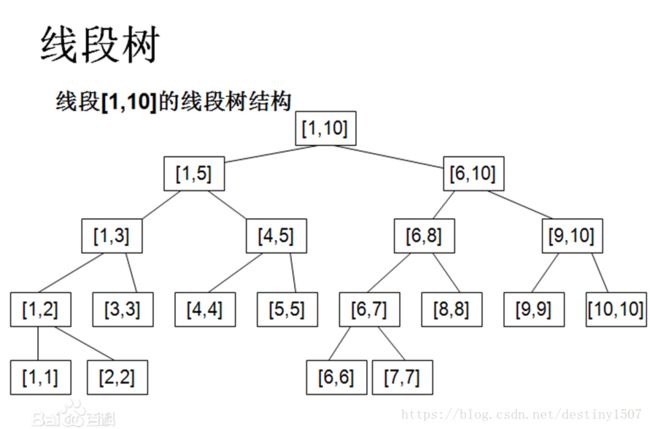
线段树的区间修改(增加tag)
感觉线段树的区间修改起来比树状数组操作简单多了(可能是我这个渣渣还不怎么理解树状数组的缘故吧T_T)
下面我们举个例子:假如我们要把一段区间的全部值+x,该怎么办;仍旧放上线段树的图便于理解(图文并茂总归好点不是)
假如我们想把[1,3]区间的值全部+2,最直观的反应就是,把表示这个区间的节点所保存的sum值+(区间长度*2),但是需要注意到的是,这个节点的父节点和子节点呢,它们的信息其实也已经改变了,所以都要进行修改,但是……这样一个一个修改的话,最坏情况下,我们要改变最大区间[1,10]的值,emmmm,怎么办,时间岂不是要炸……
这时候到了我们的tag发挥作用的时候了,其基本思想是这样的:我们的目的就是查询时拿到的值是正确的就可以了,当我们要修改某个区间的值的时候,只把这个点所保存的sum修改,就是我们上面一开始想的。然后用tag标记子节点要加多少(!=0了),说明这个点下面的子节点还没有改过,当我们查询到子节点的时候再把tag值加上。
还是举个例子,结合代码可以更好理解这个过程:
POJ - 3468
题目大意:给你一段初始序列,进行一些操作:Q l r:表示询问区间[l,r]的和,C l r x:表示把区间[l,r]的每一个数加x;
首先建树:
struct node
{
ll l,r;
ll sum,tag;
}tree[maxn<<2];
void build(ll k,ll l,ll r)
{
tree[k].l=l;tree[k].r=r;
if(l==r)//说明已经到了叶子节点,该区间表示的是一个数
{
tree[k].sum=a[l];
return;
}
ll mid=(l+r)>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);//分别建立左子树和右子树
tree[k].sum=tree[k<<1].sum+tree[k<<1|1].sum;
}
然后加数的函数:
void add(ll k,ll l,ll r,ll x)
{
if(tree[k].tag)
change(k);
tree[k].sum+=(r-l+1)*x;//先把该节点的sum值加上
if(tree[k].l==l&&tree[k].r==r)
{
tree[k].tag+=x;
return;
}//找区间做标记
ll mid=(tree[k].l+tree[k].r)>>1;
if(l>=mid+1)//一直往下找
add(k<<1|1,l,r,x);
else if(r<=mid)
add(k<<1,l,r,x);
else
{
add(k<<1,l,mid,x);add(k<<1|1,mid+1,r,x);
}
tree[k].sum=tree[k<<1].sum+tree[k<<1|1].sum;//这时子节点的之已经改变过了,根节点的sum值要重新计算一下
}其中的change函数用来修改子节点的tag值(当前节点tag值不为0,说明它的子节点还处于未被修改的状态)
change函数:
void change(ll k)
{
if(tree[k].l!=tree[k].r)
{
tree[k<<1].sum+=(tree[k<<1].r-tree[k<<1].l+1)*tree[k].tag;
tree[k<<1|1].sum+=(tree[k<<1|1].r-tree[k<<1|1].l+1)*tree[k].tag;
tree[k<<1].tag+=tree[k].tag;
tree[k<<1|1].tag+=tree[k].tag;
}
tree[k].tag=0;
}最后是查询函数:
这个跟之前的几乎一样了,不过要先修改一下子区间的值,就是先调用一下change函数
ll query(ll k,ll l,ll r)
{
ll res;
if(tree[k].tag)
change(k);
if(tree[k].l==l&&tree[k].r==r)
return tree[k].sum;
ll mid=(tree[k].l+tree[k].r)>>1;
if(r<=mid)
res=query(k<<1,l,r);
else if(l>=mid+1)
res=query(k<<1|1,l,r);
else
res=query(k<<1,l,mid)+query(k<<1|1,mid+1,r);
tree[k].sum=tree[k<<1].sum+tree[k<<1|1].sum;
return res;
}呼呼
这些其实都是模板hiahiahia,留着备用hiahiahia