聚类
聚类是一种无监督算法,针对大量未知标注的数据集,按数据的相似性将数据分为多个类别,使类别内的数据相似性较大而类别间的数据相似度较小。若数据集已知标注,则可以利用聚类对数据降维操作。
聚类算法分类:基于位置的聚类(kmeans\kmedians),基于密度的聚类(DBSCAN\最大密度聚类),基于图论的聚类(AP聚类\谱聚类)
基于位置的聚类
基于位置的聚类基本思想:对于给定的类别数目K,初始选择k个类别中心,对于每个样本,将其标记为距离类别中心最近的样本,将每个类别中心更新为隶属该类别的所有样本均值(kmedians是标记为样本中位数,优点在于抗离群点),重复操作,知道类别中心的变化小于某个阈值。终止条件可设置为迭代次数,簇中心变化率或最小平方误差。
基于位置的聚类基本思想会遇到这几个问题:
1、类别数目K如何给定
2、初值的选择
1、聚类的k值一般根据业务确定,也可以通过绘制损失函数与k值的关系,选择损失函数曲线处于拐点位置的k值(即Elbow法),即在该点随着k的增加,聚类效果并未出现显著的提升,聚类的损失函数,一般取各个簇的样本点到簇中心的距离的2范式。
2、k-mans是初值敏感的,初始簇中点的选取还有两种方法:
1-是依次选择彼此距离尽可能远的K个点 ,或多初始化几遍,选取损失函数小的一组初始样本点。以此为思想,有升级的算法Kmeans++,根据权重选取初始值(权重为样本点间的距离)。
2-是先对数据用层次聚类算法或者Canopy算法进行聚类,得到K个簇之后,从每个类簇中选择一个点,该点可以是该类簇的中心点。
层次聚类是对给定的数据集做层次的分解,直到满足某种条件,层次聚类有AGNES算法与DIANA算法,AGNES算法是一种自底向上的策略,首先将每一个样本看做一个簇,然后根据某个准则合并簇,一般是合并距离相近的簇,这里的距离一般取两个簇中距离最近的样本点的相似度,反复进行直到达到需要的簇数目,DIANA是AGNES的逆操作。
Canopy算法常做空间索引,一般用在K均值之前的粗聚类,给定两个距离阈值 T1 , T2 ,且 T1 > T2 ,随机选择一个样本点做簇中心,距离小于 T2 的划入该中心的簇,且不能作为其他簇的待选中心,大于 T2 小于 T1 的也放入该簇,但可以作为其他簇的待选中心,直到不存在距离任一簇中心距离大于 T1 的样本点。
k-means有明显的缺点:1.对初始聚类中心敏感。2.必须提前指定K值。3.属于硬聚类,每个样本点只能属于一类 。4.在均值可被定义情况下才能使用,同时对异常值免疫能力差,对噪声和孤立点数据比较敏感。5.对非球状数据处理效果并不好。
k-means最大的优点:速度快,想要收敛速度进一步加快,可以使用Mini-BatchKmeans,也就是求梯度的时候用的是随机梯度下降的方法,而不是批量梯度下降。k-means适合用于球形聚类。
对于缺失值的问题:
离散的特征:将缺失的作为单独一类,如果缺失特征较多可考虑删除该样本点。
连续的特征:其他变量对这个变量回归,做填补;样本平均值填补;中位数填补。
基于密度的聚类
密度聚类的思想,只要样本点的密度大于某阈值,则将该样本加到最近的簇中。这类算法可以克服基于距离的聚类不适用于非团状数据的缺点,同时对噪声数据也不敏感,但相对来说算法的计算复杂度也大。基于密度聚类有DBSCAN与基于密度最大值算法,基于密度的聚类不需要事先给定簇的个数。
1、DBSCAN:
DBSCAN将簇定义为密度相连的点的最大集合,这里需要了解几个概念,给定半径r与数目m,一个样本的r-领域有m个及其以上样本,称该样本为核心对象,对于落在该样本r-领域内的其他样本,可以称这些样本与核心对象关于 r,m 密度相连。由算法思想可知,非核心对象可以是簇的一部分,构成了簇的边缘。给定r不变,m越小簇的个数越多,给定m不变,r越小簇的个数越多。
2、密度最大值聚类:
密度最大值聚类里也有几个概念,给定一个超参数距离 d ,局部密度 ρi 表示到样本 i 距离小于 d 的样本数,高局部密度点距离 δi 表示局部密度大于样本 i 的样本到样本i的最短距离。那些有着比较大的局部密度 ρ 和很大的高局部密度点距离 δ 被认为是簇中心,局部密度 ρ 较小而高密距离 δ 较大的一般是离群点,二者皆小的一般是簇的边缘。
基于图论的聚类
1、AP(affinity propagation:吸引力传输)聚类:
AP算法的思想是最小化样本与所属簇质心的相似性,这里质心可理解成是簇的代表样本,算法里将样本与所属簇质心的相似性分为两部分,吸引度(responsibility) r(i,k) 值与归属度(availability) a(i,k) 值。sklearn的cluster函数库中,默认负欧式距离为相似度(affinity=’euclidean’),参数preference表示样本与本身的相似度(以本身为簇质心),默认值是中位数,damping为阻尼系数,用以构造 r 值与 a 值进行有关迭代参数的凸组合额,使得算法收敛,默认值是0.5。吸引度 r(i,k) 值用以度量样本k作为样本i所在的簇质心的可靠性,归属度 a(i,k) 值用以度量样本i隶属于以样本k为簇质心的可靠性。二者的迭代公式如下。
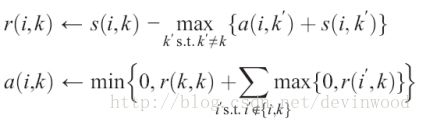
AP算法无需认为给定聚类的簇个数,但其算法空间与时间复杂度比较大,不太适合数据量过大的样本聚类。
2、谱聚类
谱聚类是一种基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,达到样本数据聚类的目的。
谱聚类需要事先给定聚类的簇,首先计算n阶相似度矩阵W(对角线为0)和度矩阵D,得到拉普拉斯矩阵 L=D−W ,游走随机拉普拉斯矩阵是
对称拉普拉斯矩阵为
计算拉普拉斯矩阵的前k个最小特征值对应的特征向量,将k个列向量组成新矩阵对每行向量做单位化处理,每一行向量即为一个样本,利用k均值对这些行向量做聚类处理。
谱聚类中的k值一般选择从小到大排列时递增幅度最大的特征值对应的k值,公式表示:
谱聚类算法在处理稀疏数据的聚类效果与高维数据聚类时的复杂度比传统聚类算法好。但由于最终聚类的维度非常高,如果降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好,同时不同的相似矩阵得到的最终聚类效果可能很不同。
聚类的衡量指标
1、均一性与完整性:
均一性(Homogeneity):一个簇只包含一个类别样本则满足均一性
完整性(Completeness):同类别样本被归到同一个簇中则满足完整性
V-measure(均一性和完整性的加权平均),输出范围在[0,1],等于1聚类效果最好。
2、ARI(原标记与聚类的列联表组合数公式) & AMI(原标记与聚类的列联表信息熵),输出范围在[0,1],等于1聚类效果最好,表示完全和标记类别相同。
3、轮廓系数 (Silhouette Coefficient )
利用簇间不相似度(与其他簇的所有样本平均值的距离最小值)与簇内不相似度(与样本所在簇的其他样本平均值距离)定义轮廓系数,
衡量指标可通过from sklearn import metrics调用

